Поворот (вращение) примитивов

Методы обработки векторной графики

В качестве устройства вывода векторных изображений могут применяться плоттеры, графопостроители и другие устройства, использующие векторный способ формирования изображений. Обработка двухмерной и трехмерной графики и трехмерной графики имеют много общего. Фактически в векторном описании изображения отсутствует третья координата — .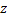

Геометрические преобразования двухмерной графики.

Будем предполагать, что мы работаем в евклидовом пространстве, где имеется ортонормированная декартова система координат, в которой координатные оси взаимно ортогональны, а соответствующие им единичные отрезки имеют одинаковую длину. Тогда каждой точке изображения ставится в соответствие упорядоченная пара декартовых координат: их можно интерпретировать как двухмерный вектор, геометрически представляемый отрезком прямой линии из точки точку.

Общее изображение включает в себя целый ряд примитивов и сегментов, отличающихся друг от друга геометрией, местоположением, ориентацией, масштабом, цветом, яркостью и другими атрибутами.

С помощью операций преобразования можно выполнять следующие действия:

- синтезировать изображения из более мелких элементов (примитивов, сегментов);

- добавлять к существующему изображению новые элементы;

- увеличивать и уменьшать размеры рисунка;

- перемещать, вращать, копировать изображения;

- создавать движущиеся изображения.

Наиболее распространенными базовыми операциями по преобразованию векторных изображений являются:

- перенос (перемещение) примитивов, сегментов и изображений;

- масштабирование (увеличение или уменьшение размеров) изображения;

- поворот изображения или его выделенных элементов (вращение, изменение ориентации).

Эти операции называются аффинными преобразованиями. Различают двухмерные и трехмерные аффинные преобразования.

Двухмерные аффинные преобразования.

Рассмотрим двухмерные аффинные преобразования, применяемые при обработке векторной графики.

Перенос примитивов.

Перенос точки.

Пусть необходимо осуществить перенос точки 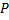с координатами 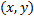, 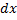- приращение координаты 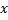, 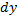- приращение координаты 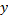. Тогда точка 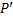с координатами 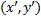будет получена после переноса (рис. 1).

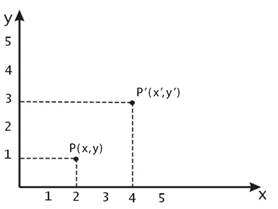
Рис. 1. Перенос точки

Новые координаты точки будут определяться соотношением

;

.

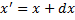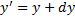Аффинные преобразования обычно записываются в матричной форме:

;

;

.

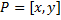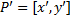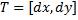Тогда .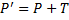

Перенос отрезка.

Перенос типа отрезка можно перенести, применяя предыдущие уравнения к каждой его точке. Все точки, принадлежащие отрезку, можно перенести путем перемещения начальной и конечной точек отрезка и последующего вычерчивания нового отрезка между получившимися в результате точками (рис. 2). Это справедливо также для масштабирования и поворота.

;

;

;

.

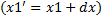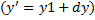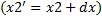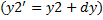Рис. 2. Перенос отрезка

В матричной форме эти преобразования можно представить в следующем виде:

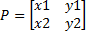– исходный отрезок;

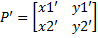– полученный отрезок;

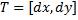– вектор переноса.

Итоговый вид преобразования в векторной форме .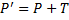

Масштабирование.

Масштабирование выполняется умножением координат на некоторые коэффициенты , .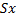

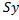Масштабирование точки.

Пусть дана точка .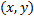

Тогда в результате масштабирования получим следующие координаты:

;

;

;

.

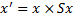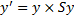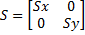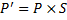Масштабирование отрезка.

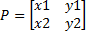– исходный отрезок;

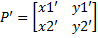– полученный отрезок;

;

.

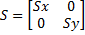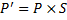Масштабирование бывает:

- однородное, когда ;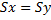

- неоднородное, когда .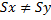

При неоднородном масштабировании фигура может изменяться (круг - эллипс).

Масштабирование также делится по значению коэффициента масштабирования (рис.3, 4).

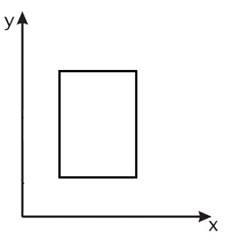
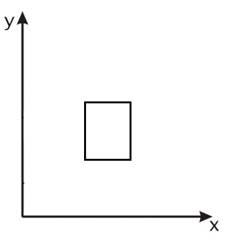
Рис. 3. Масштабирование с коэффициентом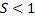

Рис. 4. Масштабирование с коэффициентом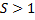

Поворот (вращение) примитивов.

Пусть необходимо осуществить поворот точки 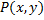на угол 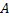(рис. 5).

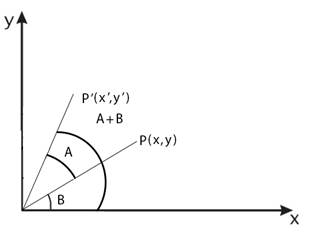
Рис. 5. Поворот в плоскости системы координат

Исходные координаты точки:

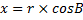; (1.1)

.

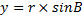После поворота точка 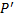будет иметь координаты:

;

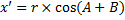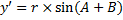. (1.2)

Преобразуем выражение (2.2):

;

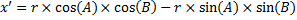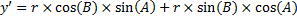. (1.3)

Подставим (1.1) в (1.3):

;

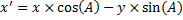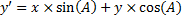. (1.4)

В матричной форме поворот записывается следующим образом:

;

;

.

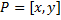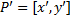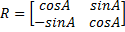Тогда в векторной форме .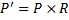

Поворот считается положительным ( 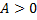), если он осуществляется против часовой стрелки; отрицательным – если по часовой.

Рассмотрим пример вычисления матрицы композиции двухмерных аффинных преобразований.

Пусть задан отрезок, определенный координатами:

.

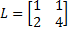1. Перенос , :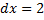

.

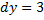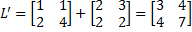2. Масштабирование :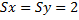

.

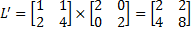3. Поворот 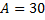градусов:

.
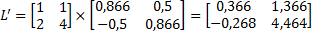