Метод простой итерации
Министерство образования Республики Беларусь
Учреждение образования
«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ»
Институт информационных технологий
МЕТОДИЧЕСКОЕ ПОСОБИЕ
(практикум)
Алгоритмы вычислительной математики
для слушателей курсов
по переподготовке и повышению квалификации
Минск 2009
УДК 621.3.6
А.Г.Корбит, Т.М.Кривоносова. . Практикум по курсу “Алгоритмы вычислительной математики”: Методическое пособие для слушателей курсов по переподготовке и повышению квалификации
Мн.: ИИТ БГУИР, 2009.- 35 с.
Общий курс “Вычислительная математика” содержит ряд разделов. Данное пособие посвящено изучению раздела курса “Основы численных методов”. В нём студентам предлагается выполнить пять индивидуальных заданий, охватывающих основные, хорошо изученные задачи. Предполагается также получить навыки программной реализации методов сортировки и ознакомиться с современными алгоритмами обработки нелинейных структур данных.
Составители: Корбит А.Г., Кривоносова Т.М.
ÓИИТ БГУИР, 2009
СОДЕРЖАНИЕ
| ЗАДАНИЕ 1 Численное решение алгебраических уравнений | |
| ЗАДАНИЕ 2. Аппроксимация функций | |
| ЗАДАНИЕ 3. Алгоритмы численного интегрирования | |
| ЗАДАНИЕ 4. Сортировка данных и поиск | |
| ЗАДАНИЕ 5. Деревья, «ПОЛИЗ», Хеширование | |
| ЛИТЕРАТУРА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| ПРИЛОЖЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
З А Д А Н И Е 1. Численное решение алгебраических уравнений
Цель работы: изучить численные методы решения алгебраических уравнений при помощи итерационных методов. Научиться программировать итерационные алгоритмы решения алгебраических уравнений с заданной точностью.
Краткие теоретические сведения
Пусть дана некоторая функциональная зависимость y=f(x) на заданном отрезке [a,b]. Решение уравнения y=f(x) заключается в поиске таких значений x*, при которых функция f(x) обращается в ноль, т.е. решение уравнения:
f(x*)=0. (1.1)
Но точное решение удается получить только в исключительных случаях, и обычно для нахождения корней уравнения применяются численные методы.
Решение уравнения (1.1) при этом осуществляется в два этапа:
1. Приближенное определение местоположения корней - этап отделения корней (нахождение грубых корней).
2. Вычисление выбранного корня с заданной точностью e. Это, как правило, итерационные методы.
Первая задача чаще всего решается графическим методом: на заданном отрезке [a, b] вычисляется таблица значений функции с некоторым шагом h, строится ее график и определяются интервалы 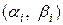 длиной h, на которых находятся корни.
длиной h, на которых находятся корни.
Вычисление значения простого корня с заданной точностью осуществляется одним из итерационных методов.
Метод простой итерации
Уравнение (2.1) записывают в виде разрешенном, относительно x:
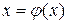 . (1.2)
. (1.2)
Заметим, что переход от записи уравнения (1.1) к эквивалентной записи (1.2) можно сделать многими способами, например, положив
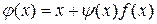 , (1.3)
, (1.3)
где 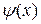 - произвольная, непрерывная, знакопостоянная функция. Часто достаточно выбрать функцию
- произвольная, непрерывная, знакопостоянная функция. Часто достаточно выбрать функцию 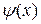 как константу y=const из диапазона ±0.1 - 0.9 .
как константу y=const из диапазона ±0.1 - 0.9 .
В этом случае корни уравнения (1.2) являются также корнями (1.1), и наоборот.
Исходя из записи (1.2) члены рекуррентной последовательности в методе простой итерации вычисляются по закону
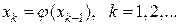 . (1.4)
. (1.4)
Метод является одношаговым, так как последовательность x0, x1, …, xк имеет первый порядок (m=1) и для начала вычислений достаточно знать одно начальное приближение 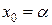 или
или 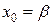 или
или 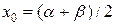 .
.
 Условием сходимости метода простой итерации: если
Условием сходимости метода простой итерации: если 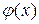 дифференцируема и выполнение неравенства
дифференцируема и выполнение неравенства 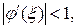 для любого
для любого 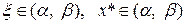 . (1.5)
. (1.5)
Максимальный интервал (a, b), для которого выполняется неравенство (1.5), называется областью сходимости.
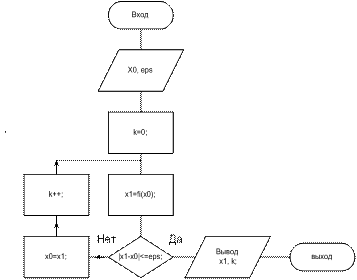
Рис. 1.1.
Схема алгоритма метода простой итерации представлена на рис. 1.1.
