Инструкция пользователя

Для запуска программы нужно запустить файл Max_potоk.exe.

Для поиска максимального потока в сети необходимо выполнить следующие действия:

1) ввести количество вершин сети (n) в поле “Количество” и нажать кнопку “Количество вершин”. В зависимости от количества вершин изменятся размеры таблиц, которыми задаются матрицы пропускных способностей и максимального потока сети. Количество вершин не может превышать 10. На рисунках 3.2(а) та 3.2(б) представлен вид этих таблиц при n=8 та n=3 соответственно.

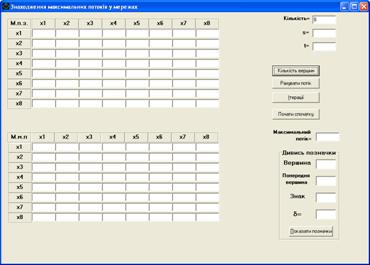
а

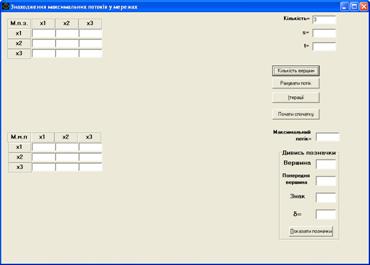б

Рис. 3.2.

2) заполнить матрицу пропускных способностей и указать номера вершин, которые будут началом (поле “s=”) и концом (поле “t=”) сети (рис. 3.3). Введение этих данных является обязательным условием для продолжения роботы программы;

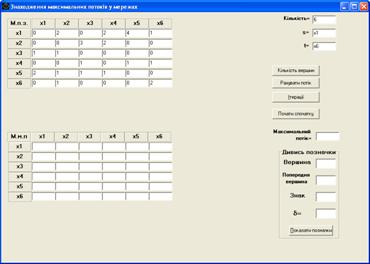
Рис. 3.3.

3) рассчитать поток:

– если для выполнения этого этапа использовать кнопку “Считать поток”, то в таблице для представления матрицы максимального потока результат отображается немедленно, а в поле “Максимальный поток” при этом отображается величина максимального потока (рис. 3.4);

– если использовать кнопку “Итерации”, то в таблице для представления матрицы максимального потока результат отображается постепенно, в зависимости от насыщения и перераспределения потока в сети. Когда поток станет максимальным – кнопка больше не буде исполнять ни одних действий (рис. 3.5). Для выведения величины максимального потока в поле “Максимальный поток” нужно нажать кнопку “Считать поток”;

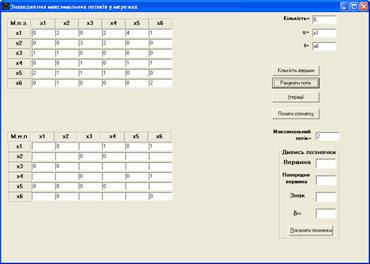
Рис. 3.4.

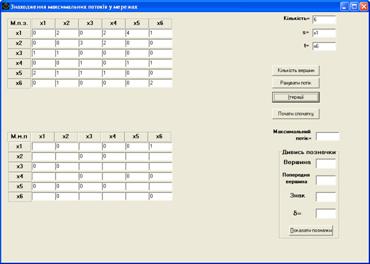
Рис. 3.5.

С помощью программы можно совершить дополнительные действия:

1) просмотреть пометки какой-либо вершины. Для этого нужно:

- задать вершину, для которой нужно вывести пометки (поле “Вершина”);

- нажать кнопку “Показать пометки”. При этом в поле “Предыдущая вершина” появится имя предыдущей вершины; в поле “Знак” появится знак “+”, если направление дуги совпадает с направлением потока, или “-“ – в противоположном случае; в поле “δ” – величина увеличения потока по данной дуге (рис. 3.6);

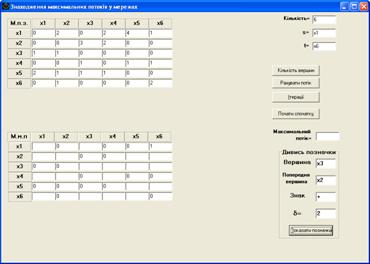
Рис. 3.6.

2) сделать таблицу матрицы максимального потока пустой. Для этого нужно нажать кнопку “Начать сначала”, но таблица матрицы пропускных способностей останется неизменной (рис. 3.7);

3) работать с новой сетью и с новой матрицей пропускных способностей. Для этого нужно ввести новое количество вершин, нажать кнопку “Количество вершин” и обе матрицы и все поля станут пустыми.

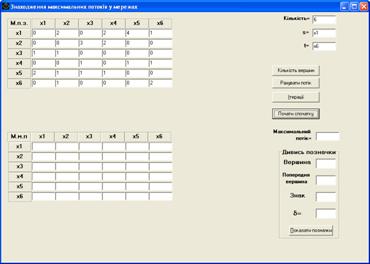
Рис. 3.7.

Реализация программы

Сравним результаты вычислений с помощью программы и вручную. Для ручного способа вычислений будем использовать алгоритм Форда-Фалкерсона.

1. Возьмём поток, изображённый на рисунке 3.8 как начальный допустимый поток. Он имеет величину 3.

2. Присвоим источнику, вершине v₁, пометку (+, ∞). Вершина v₁ помечена, но не просмотрена.

3. Просмотрим вершины, смежные с вершиной v₁. Вершине v₂ присвоим пометку (+v₁, 1), а вершине v₃ – пометку (+v₁, 1),т.к. φ(v₁, v₂) = 2 < 3 = с₁, φ(v₁, v₃) = 1 < 2 = с₂. Вершина v₁ помечена и просмотрена, а вершины v₂ и v₃ помечены, но не просмотрены.

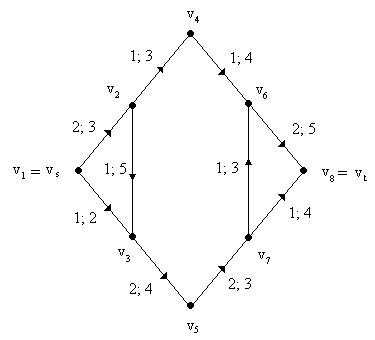
Рис. 3.8. Поток величины 3

4. Просмотрим вершины, смежные с вершиной v₂. Из вершин, смежных с вершиной v₂, не помечена только вершина v₄. Вершине v₄ присваиваем пометку (+v₂, 1), поскольку φ(v₂, v₄) = 1 < 3 = с₃.

5. Просмотрим вершины, смежные с вершиной v₃. Из вершин, смежных с вершиной v₃, не помечена только вершина v₅. Вершине v₅ присваиваем пометку (+v₃, 1), поскольку φ(v₃, v₅) = 2 < 4 = с₄.

6. Просмотрим вершины, смежные с вершиной v₄. Смежной и непомеченной является вершина v₆. Присваиваем ей пометку (+v₄, 1), поскольку φ(v₄, v₆) = 1 < 4 = с₅.

7. Просмотрим вершины, смежные с вершиной v₅. Смежной и непомеченной является вершина v₇. Присваиваем ей пометку (+v₅, 1), поскольку φ(v₅, v₇) = 2 < 3 = с₆.

8. Просмотрим вершины, смежные с вершиной v₆. Смежной и непомеченной является вершина v₈. Присваиваем ей пометку (+v₆, 1), поскольку φ(v₆, v₈) = 2 < 5 = с₇. Сток помечен. Переходим к операции Б – увеличению потока.

9. Сток имеет пометку (+v₆, 1). Поэтому увеличиваем поток по дуге (v₆, v₈) на 1.

10. Вершина v₆ имеет пометку (+v₄, 1). Поэтому увеличиваем поток по дуге (v₄, v₆) на 1.

11. . Вершина v₄ имеет пометку (+v₂, 1). Поэтому увеличиваем поток по дуге (v₂, v₄) на 1.

12. . Вершина v₂ имеет пометку (+v₁, 1). Поэтому увеличиваем поток по дуге (v₁, v₂) на 1. Мы получили новый поток величины 4 (рис. 3.9).

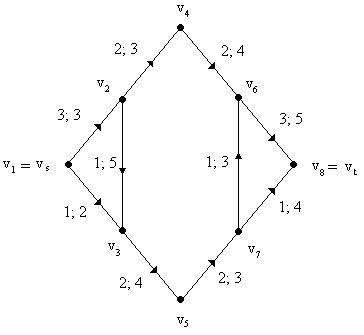
Рис. 3.9. Поток величины 4

13. Стираем все пометки.

14. Присваиваем вершине v₁ пометку (+, ∞).

15. Просмотрим вершины, смежные с вершиной v₁. Вершину v₂ не помечаем, поскольку φ(v₁, v₂) = 3 = c(e₁), а вершинеv₃ присваиваем пометку (+v₁, 1).

16. Просмотрим вершины, смежные с вершиной v₃. Вершине v₂ присваиваем пометку (-v₃, 1), поскольку φ(v₂, v₃) = 1 > 0, l(v) = 1 и min(1, 1) = 1, а вершине v₅ припишем пометку (+v₃, 1), так как φ(v₃, v₅) = 2 < 4 = c₈.

17. Просмотрим вершины, смежные с вершиной v₄. Вершине v₆ присваиваем пометку (+v₄, 1), поскольку φ(v₄, v₆) = 3 < 5 = с₉.

18. Просмотрим вершины, смежные с вершиной v₅. Вершине v₇ присваиваем пометку (+v₅, 1), поскольку φ(v₅, v₇) = 2 < 3 = с₁₀.

19. Просмотрим вершины, смежные с вершиной v₆. Вершине v₈ присваиваем пометку (+v₆, 1), поскольку φ(v₆, v₈) = 3 < 5 = с₁₁. Сток помечен. Переходим к операции Б – увеличению потока.

20. Сток имеет пометку (+v₆, 1). Поэтому увеличиваем поток по дуге (v₆, v₈) на 1.

21. Вершина v₆ имеет пометку (+v₄, 1). Поэтому увеличиваем поток по дуге (v₄, v₆) на 1.

22. Вершина v₄ имеет пометку (+v₂, 1). Поэтому увеличиваем поток по дуге (v₂, v₄) на 1.

23. Вершина v₂ имеет пометку (-v₃, 1). Поэтому уменьшаем поток по дуге (v₂, v₃) на 1.

24. Вершина v₃ имеет пометку (+v₁, 1). Поэтому увеличиваем поток по дуге (v₁, v₃) на 1. Получили новый поток величины 5 (рис. 3.10).

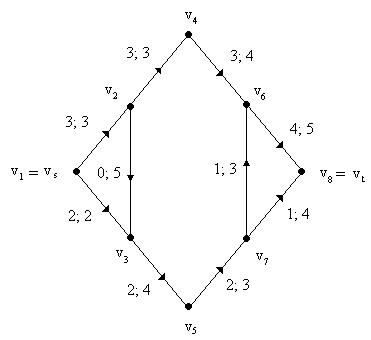
Рис. 3.10. Поток величины 5

25. Стираем все пометки.

26. Присваиваем вершине v₁ пометку (+, ∞).

27. Вершины, смежные вершине v₁, нельзя пометить, поскольку дуга (v₁, v₂) насыщена – φ(v₁, v₂) = φ(е₁) = с(е₁) = 3, и дуга (v₁, v₃) тоже насыщена – φ(v₁, v₃) = φ(е₂) = с(е₂) = 2. Сток остался непомеченным. Значит, полученный поток максимален.

А теперь найдём максимальный поток с помощью программы. Для этого введём матрицу пропускных способностей в соответствующие поля программы. Матрица имеет следующий вид:

Результат вычислений оказался тем же. Мы получили максимальный поток величины 5 (рис. 3.11).

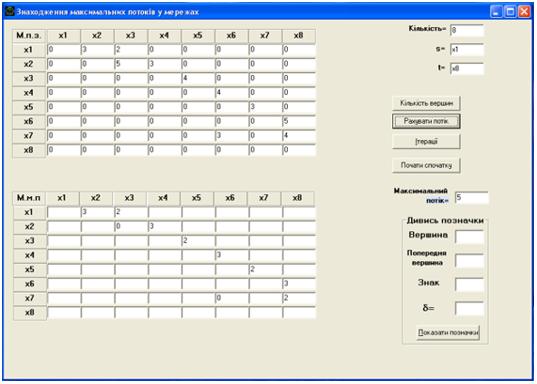
Рис. 3.11.