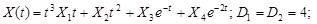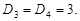Линейные преобразования случайных функций

Говорят, что случайная функция Х(t) сходится в среднеквадратическом при 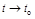к случайной величине Х_о, если начальный момент второго порядка 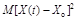стремится к нулю при t ® t_о:

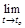
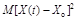= 0.

Сходимость в среднеквадратическом обозначается символом

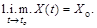
Случайная функцияХ(t) называется непрерывной в среднеквадратическом в точке t_о, если

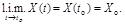
Производной случайной функции X(t) называется случайная функция X¢(t), определяемая как предел в среднеквадратическом отношения приращения случайной функции к приращению неслучайного аргумента:

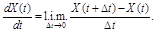
Для дифференцируемости случайной функции необходимо, чтобы функция X(t)была непрерывной, а для этого непрерывной должна быть ее корреляционная функция. Достаточным условием дифференцируемости функции X(t)в точке t является существование второй смешанной частной производной корреляционной функции при равных значениях ее аргументов.

Интегралом в среднеквадратическом от случайной функции X(t) в постоянных границах от a до b называется предел соответствующей интегральной суммы

,

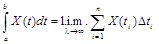где l- наибольший из всех Dt_i, а предел понимается в смысле среднеквадратического.

Линейным однородным преобразованием случайной функции X(t) называется преобразование L_о, обладающее следующими свойствами:

1^о. L_о[X₁(t) + X₂(t)]= L_о[X₁(t)] + L_о[X₂(t)];

2^о. L_о[CX(t)] = CL_о[X(t)].

Примерами линейных однородных преобразований могут служить:

а) оператор дифференцирования ;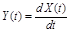

б) оператор интегрирования ,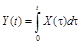

где операции дифференцирования и интегрирования следует понимать в «среднеквадратическом»;

в) оператор умножения случайной функции на неслучайную

Y(t) = j(t)X(t);

г) оператор интегрирования с заданным «весом» .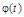

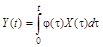Линейным неоднородным называется преобразование вида

Y(t) = L_о[X(t)] + f(t),

где f(t)- неслучайная функция.

Каноническим разложением случайной функции называется сумма ее математического ожидания и взаимно некоррелированных элементарных случайных функций

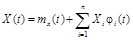, (9.4)

где случайные величины 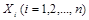имеют математические ожидания, равные нулю, и называются коэффициентами канонического разложения, а неслучайные функции 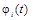- координатными функциями.

Корреляционная функция канонического разложения имеет вид

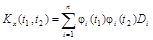. (9.5)

При t₁ = t₂ = t 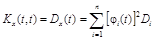. (9.5а)

9.17.На RC - цепочку, изображённую на рис. 9.1, подаётся

случайное напряжение X(t) c характеристикам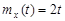и и 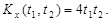Найти математическое ожидание, корреляционную функцию и дисперсию напряжения Y(t) на выходе цепочки.

¢ Дифференциальное уравнение, описывающее связь между входным и выходным напряжениями RC - цепочки, составляется на основе закона Кирхгофа и имеет вид

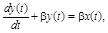
Решая это уравнение при нулевом начальном условии методом вариации произвольных постоянных, получим:

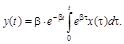
Таким образом, случайный процесс Y(t) является результатом применения к случайной функции X(t) линейного однородного оператора

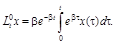
Значит,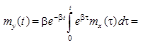

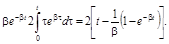
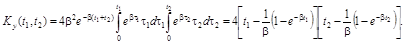Дисперсия процесса на выходе равна . £

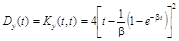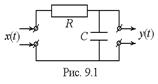
9.18.На вход дифференцирующего устройства поступает случайный процесс X(t) с математическим ожиданием 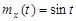и корреляционной функцией 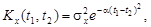где 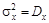- постоянная дисперсия X(t). Определить математическое ожидание и дисперсию на выходе системы.

¢ Реакция 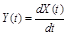имеет характеристики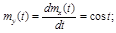

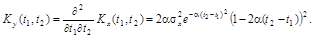
Полагая 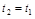, находим дисперсию 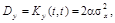которая зависит от 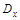и от коэффициента 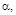характеризующего быстроту затухания корреляционной связи между сечениями случайной функции X(t) при возрастании промежутка между ними.

При малых значениях 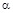корреляционная связь затухает медленно, поэтому случайные функции X(t) и Y(t) изменяются со временем сравнительно плавно. Следовательно, дифференцирование X(t) приводит к незначительным ошибкам.

Если же величина 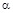велика, корреляционная функция 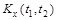убывает быстро, в составе случайной функции X(t) преобладают резкие беспорядочные колебания, значит, дифференцирование такой функции приведет к большим погрешностям. £

9.19.Случайная функция X(t) задана каноническим разложением:

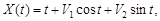
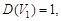
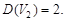
Найти математическое ожидание, дисперсию и корреляционную функцию процесса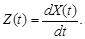

¢ Запишем каноническое разложение случайного процесса Z(t):

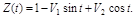
Отсюда следует, что 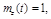координатные функции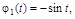

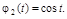
Каноническое разложение корреляционной функции 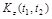имеет вид

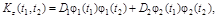
или .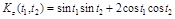

Тогда дисперсия процесса будет равна £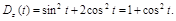

9.20 – 9.29. На вход динамической системы поступает случайный сигнал X(t), характеристики которого известны. Работа системы описывается оператором L. Определить характеристики случайной функции Y(t).

9.20.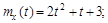

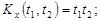
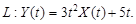
9.21.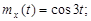

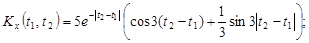
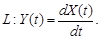
9.22.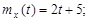

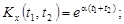
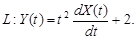
9.23.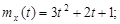

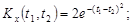
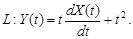
9.24.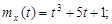

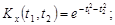
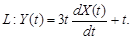
9.25.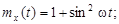

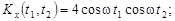
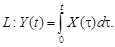
9.26.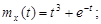

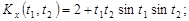
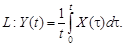
9.27.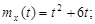

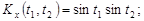
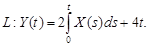
9.28.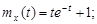

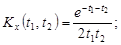
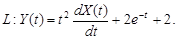
9.29.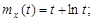

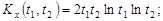
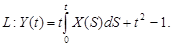
9.30 – 9.34. Найти характеристики случайной функции X(t), заданной своим каноническим разложением.

9.30.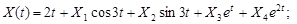

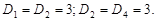
9.31.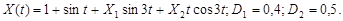

9.32.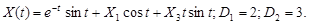

9.33.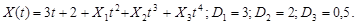

9.34.