О способе вспомогательных концентрических сфер
Если оси поверхностей вращения пересекаются в пределах чертежа и расположены в плоскостях уровня, то для построения линии пересечения поверхностей можно применить способ вспомогательных секущих сфер
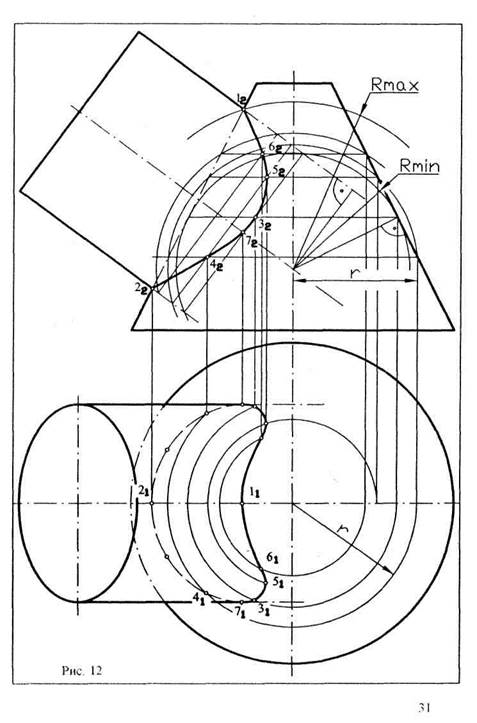
Рассмотрим применение способа на следующем примере. Заданы конус и цилиндр (рис. 12). Требуется построить линию их пересечения.
Построив на чертеже очевидные точки 1 и 2, выбираем поверхности-посредники для построения остальных интересующих нас точек Заметим 26
 |
 |
 |
что оси цилиндра и конуса пересекаются и лежат во фронтальной плоскости. в таком случае целесообразно применять секущие сферические поверхности
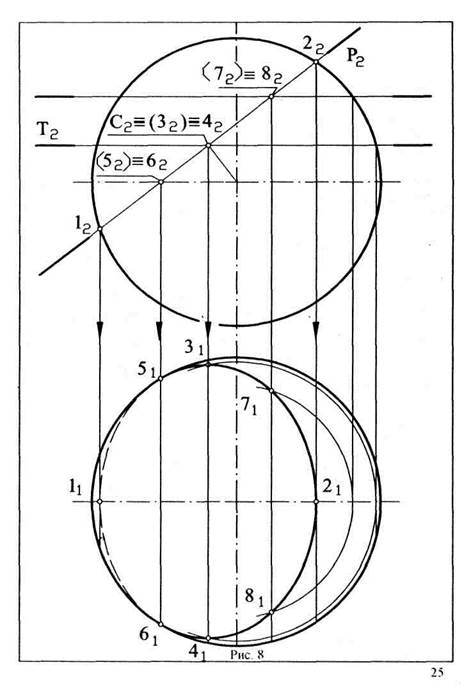
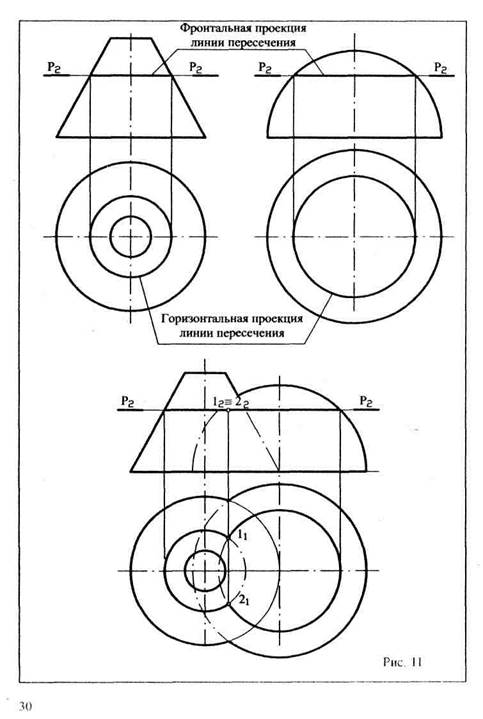
Точку пересечения осей цилиндра и конуса примем за центр сферы произвольного радиуса. Фронтальная проекция такой сферы представит собой окружность того же радиуса. Проведем ее. Сфера соосна и конусу, и цилиндру. Она пересекается с ними по окружностям, которые на фронтальной проекции изобразятся отрезками прямых. В пересечении этих окружностей получим точки, принадлежащие обеим данным поверхностям.
Беря сферы различных радиусов, можно получить сколько угодно точек линии пересечения. Однако перед тем как начинать построение, необходимо определить размеры максимального и минимального радиусов сфер. применимых для решения этой задачи. Чтобы определить радиус Rmin наименьшей сферы, которая пересекает обе поверхности, нужно из точки пересечения осей фигур опустить перпендикуляры на очерковые образующие цилиндра и конуса и взять наибольший из них. Сфера меньшего радиуса окажется внутри одной из поверхностей и не пересечется с ней и. следовательно, полезной быть не может.
Радиус Rmax наибольшей сферы определяется расстоянием от точки пересечения осей до наиболее удаленной от нее точки пересечения очерковых образующих (на рис. 5 это точка 12).
Используя сферы различных радиусов (в пределах между Rmax и Rmin).
построим ряд промежуточных точек линии пересечения и соединим их плавной кривой. Построив линию видимого контура, нетрудно заметить, что невидимая часть кривой полностью сливается с видимой, так как они симметричны.
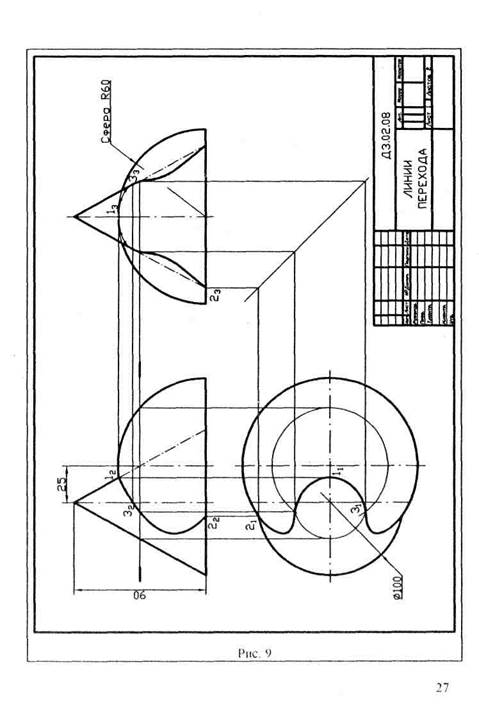
Для построения горизонтальной проекции линии пересечения используются окружности, полученные ранее при пересечении конуса со сферой. На горизонтальную плоскость проекций они проецируются без искажения. Проведя линии проекционной связи из соответствующих фронтальных проекций точек до пересечения с этими окружностями, получаем горизонтальные проекции линии пересечения. На горизонтальной проекции необходимо также определить точки, лежащие на очерковых образующих цилиндра и делящие кривую на видимую и невидимую части. Для этого отмечаем их на построенной фронтальной проекции кривой (точка 7 и ей симметричная относительно оси цилиндра) и уже затем при помощи линии проекционной связи находим их горизонтальные проекции. Точки 71, 31, 51, 61, I1 и им симметричные соединяем линией видимого контура, а остальные точки линии пересечения - линией невидимого контура.
 |
 |
 |
 |
 |
 |
I
