Системы линейных алгебраических уравнений.
Сначала решим задачи с помощью матричного метода и с помощью метода Крамера.
Задача 3.Решить систему линейных уравнений:
Решение.
А. Матричным методом.
Запишем систему в виде: 
.
Домножим на обратную матрицу слева обе части равенства, для этого сначала найдём обратную матрицу.
Выполним действия, необходимые для поиска обратной матрицы
Умножим 
.
= 
= 
= 
.
Итак, получили 
.
Б. Методом Крамера.
= 
= 
.
Ответ. .
Задача 4.Решить систему линейных уравнений:
Решение.
А. Матричным методом.
Запишем систему в виде: 
.
Найдём обратную матрицу для А.
.
= 
= 
= 
.
Б. Методом Крамера.
= 
= 
.
Ответ. 
.
Метод Гаусса.
Задача 5. Решить систему уравнений 
Решение.
Построим расширенную матрицу системы и преобразуем её.
чтобы обнулились коэффициенты ниже левого верхнего угла, то есть чтобы исчезла переменная 
из всех уравнений кроме первого, надо:
а) из 2-й строки вычесть 1-ю;
б) из 3-й строки вычест удвоенную 1-ю.
= 
Теперь, чтобы обнулить ниже чем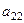 
, нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.
= 
Когда в основной матрице уже получена треугольная структура, снова перепишем в виде системы
В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить 
. Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.
.
А теперь уже две последних неизвестных стали известны, и с этой информацией поднимаемся в 1-е уравнение, подставляя туда и 
. Итак, 
.
Ответ. 
=2, 
=1, 
=1.
Можно ответ записать и в виде вектора: 
.
Задача 6. Решить систему уравнений 
Решение.Во-первых, можно всё 2-е уравнение сократить на 2, так удобнее для решения, числа будут меньше. Затем обнуляем ниже углового элемента: вычитаем из 2-го уравнения удвоенное 1-е, а также 3-го 1-е.
=
треугольная структура уже получилась.
Перепишем снова в виде системы:
из 3-го уравнения 
, подставляем во 2-е, там получается 
.
А из 1-го 
.
Ответ. 
, , .
Задача 7. Решить систему уравнений 
Решение.
При построении расширенной матрицы, сразу же домножим 2-е и 3-е уравнения на такие коэффициенты, чтобы в начале строки были числа, кратные угловому элементу. А именно, 2-ю строку на 2, а 3-ю строку на 4. Так надо, чтобы потом в методе Гаусса можно было не домножать на дробные коэффициенты при вычитании строк.
Теперь вычтем из 2-й строки 1-ю, домноженную на 3,
а из 3-й строки 1-ю, домноженную на 5.
= 
Если теперь поменять местами 2 и 3 строки, получится:
система: 
И хотя матрица не выглядит как матрица треугольного вида, тем не менее, основная идея метода Гаусса уже реализована: чем ниже, тем меньше переменных, а в последнем уравнении всего одна, а именно 
. Здесь тоже можно последовательно выразить все переменные, просто начинаем не с последней, а в другом порядке. К треугольному виду в этом случае можно до конца и не приводить.
Итак, из третьего: 
, то есть 
.
Подставляем во второе уравнение. 
, т.е. 
, 
.
Из первого: 
, откуда 
, 
.
Ответ. , , .