Лекция 7. Сложное сопротивление

Сложным сопротивлением называются виды нагружения, при которых в поперечных сечениях одновременно действуют несколько внутренних силовых факторов.

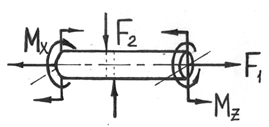
Рис.7.1

Сложный вид деформации можно рассматривать как сумму простых видов, изученных ранее (растяжение, изгиб, кручение), при которых в сечениях элементов конструкций возникал только один внутренний силовой фактор (рис.7.2): нормальная сила N - при растяжении, изгибающий момент М_z - при чистом изгибе, крутящий момент М_x - при кручении. Эти виды нагружения, растяжение, изгиб, кручение, являются простыми.

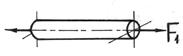
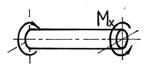
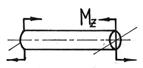
Рис.7.2

Основные соотношения, полученные для них, приведены в таблице 7.1

Таблица 7.1

Виды нагружения	Напряжения	Деформации
Растяжение	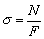. Условие прочности:
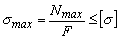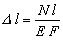Изгиб	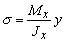. Условие прочности:
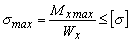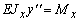Кручение	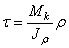. Условие прочности:

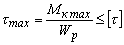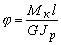Но при сложном сопротивлении должен быть применим принцип независимости действия сил (частный случай принципа суперпозиции или наложения, применяемый в механике деформируемого твердого тела).

Напомним формулировку принципа независимости действия сил: напряжение (деформация) от группы сил равно сумме напряжений (деформаций) от каждой силы в отдельности. Он справедлив, если функция и аргумент связаны линейной зависимостью. В задачах механики материалов и конструкций становится неприменимым, если:

- напряжения в какой-либо части конструкции от одной из сил или группы сил превышают предел пропорциональности ;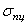

- деформации или перемещения становятся настолько большими, что нарушается линейная зависимость между ними и нагрузкой.

Например, дифференциальное уравнение изгиба стержня является нелинейным и вытекающая из него зависимость прогиба f от нагрузки Р для консольной балки, изображенной на рис.7.3, а, также является нелинейной (рис.7.3, б). Однако, если прогибы балки невелики ( 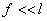) настолько, что 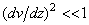(так как 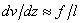), то дифференциальное уравнение изгиба становится линейным (как видно из рис.7.3, б, начальный участок зависимости Р от f, описываемый этим уравнением, также является линейным).

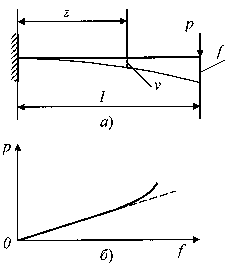
Рис.7.3. Модели изгиба балки: а) расчетная схема

б) линейное и нелинейное сопротивления

Задачи на сложное сопротивление решаются следующим образом. Определяются напряжения и деформации при действии простейших видов деформации, составляющих сложное сопротивление, а затем полученные результаты суммируют, используя при необходимости теории прочности.

На практике одновременное действие всех силовых факторов встречается крайне редко. Чаще приходится иметь дело с более простыми комбинациями нагружений – косой или пространственный изгиб, внецентренное растяжение или сжатие и изгиб с кручением.