Построение парного линейного уравнения регрессии

Решение типовых задач

Расчет парного линейного коэффициента корреляции

Для иллюстрации возможностей табличного редактора Excel в отношении построения коэффициента корреляции используем данные представленные в таблице 2.1

Таблица 2.1 – Вариация инвестиций в основной капитал и среднегодовой численности занятых в разрезе муниципальных образований Оренбургской области в 2014 году

	Y	X		Y	X
Абдулинский			г.Бузулук
Адамовский			г.Гай
Акбулакский			г.Кувандык
Александровский			г.Медногорск
Асекеевский			г.Новотроицк
Беляевский			г.Оренбург
Бугурусланский			г.Орск
Бузулукский			г.Соль-Илецк
Гайский			г.Сорочинск
Грачевский			г.Ясный
Домбаровский			г.Бугуруслан
Илекский			Пономаревский
Кваркенский			Сакмарский
Красногвардейский			Саракташский
Кувандыкский			Светлинский
Курманаевский			Северный
Матвеевский			Соль-Илецкий
Новоорский			Сорочинский
Новосергиевский			Ташлинский
Октябрьский			Тоцкий
Оренбургский			Тюльганский
Первомайский			Шарлыкский
Переволоцкий			Ясненский
Пономаревский			г.Абдулино
Сакмарский			г.Бугуруслан
Саракташский			г.Бузулук
Светлинский			г.Гай
Северный			г.Кувандык
Соль-Илецкий			г.Медногорск
Сорочинский			г.Новотроицк
Ташлинский			г.Оренбург
Тоцкий			г.Орск
Тюльганский			г.Соль-Илецк
Шарлыкский			г.Сорочинск
Ясненский			г.Ясный
г.Абдулино			-	-	-
Примечание: Y - инвестиции в основной капитал, тыс. руб.; X - среднегодовая численность работников организаций, чел. Источник: Города и районы Оренбургской области. 2015: стат.сб. / Оренбургстат. – Оренбург: 2015. – 254 с.

Шаг 1. Для построения показателя, необходимо в главном меню выбрать Данные / Анализ данных.

Шаг 2. В появившемся окне Анализ данных(рисунок 2.1) выберемпунктКорреляция.

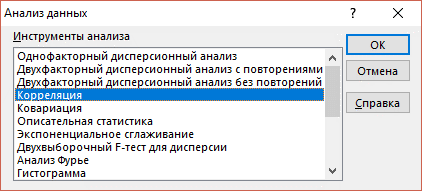
Рисунок 2.1 - Окно выбора метода обработки данных

Шаг 3. В окне Корреляция, необходимо выделить диапазон (Входной интервал)в который входят значения изучаемых показателей, для этого необходимо нажать кнопку .

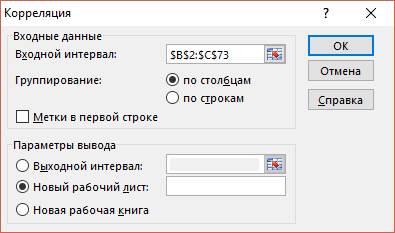
Рисунок 2.2 – Выделение диапазона анализа

Результатом работы процедуры оценивания коэффициентов корреляции является матрица (рисунок 2.3).

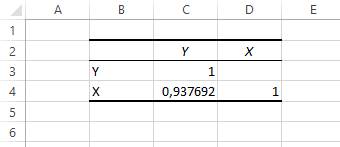
Рисунок 2.3 – Результаты построения матрицы парных коэффициентов корреляции

Данная матрица семерична относительно главной диагонали, поэтому приводится только одна из половин. В первом столбце стоят значения парных коэффициентов корреляции, отражающие зависимость между Y и факторами X.

Полученное значение равно 0,94, что указывает на сильную прямую взаимосвязь между анализируемыми показателями.

Построение парного линейного уравнения регрессии

В табличном редакторе Excel находится огромное количество встроенных функция (математические, статистические, финансовые и др.) все они предназначены для того, чтобы облегчить исследователю расчет некоторых формул.

Рассмотрим некоторые важные статистические функции необходимые для построения регрессионных моделей.

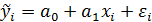
где 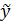- значения полученные в результате построения регрессионной модели (теоретические уровни, модельные данные)

x – независимая переменная;

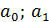– а₀, а₁, …, а_k - искомые (неизвестные) параметры (коэффициенты) уравнения регрессии;

Шаг 1. Для вставки необходимой функции в главном меню выберем Формулы / Встроить функцию(рисунок 2.4).

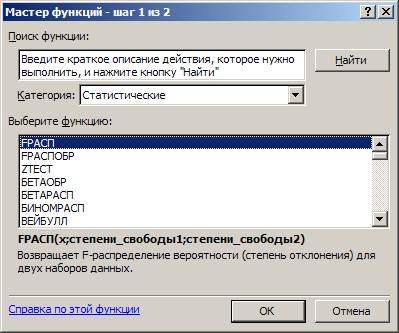
Рисунок 2.4 – Окно выбора необходимой функции

Шаг 2. Для определения параметров линейного и параболического тренда служит функция ЛИНЕЙН. Синтаксис данной функции следующий:

ЛИНЕЙН(известные_значения_y;известные_значения_x;конст;статистика)

Конст - логическое значение, которое указывает, требуется ли, чтобы параметр а₀ был равен нулю.

Если конст имеет значение ИСТИНА или опущено, то а₀ вычисляется обычным образом.

Если аргумент конст имеет значение ЛОЖЬ, то а₀ полагается равным 0 и значения a подбираются так, чтобы выполнялось соотношение 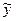= ax.

Статистика — логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии.

Если аргумент статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику, так что возвращаемый массив будет иметь вид: {а_m;a_m-1;...;а₀:se_m;se_m-1;...;se₁;se₀:R²;se_y:F;df:ss_reg;ss_resid}.

Если аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН возвращает только коэффициенты a и постоянную а₀.

Более подробную информацию по данной функции можно получить в Excel, для этого можно воспользоваться встроенной справкой.

Шаг 3. Вводим в поле табличного редактора формулу, как показано на рисунке 2.5.

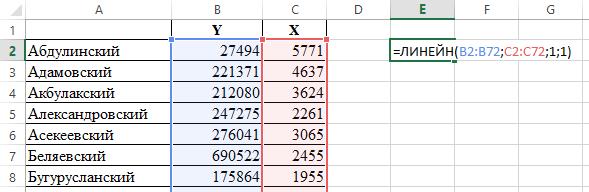
Рисунок 2.5 – Расчет параметров линейной регрессии с применением функции ЛИНЕЙН

ВНИМАНИЕ: очень важно указать два последних параметра как 1 и 1, в противном случае часть показателей не будет рассчитана.

Шаг 4. Выделяем диапазон ячеек E2:F6, далее нажимаем клавишу F2, затем сочетание славишь Ctrl+Shift+Enter (ввод массива данных) в итоге получаем результаты представленные на рисунке 2.6.

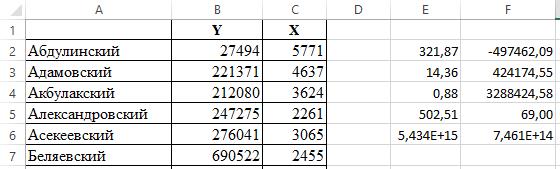
Рисунок 2.6 – Результаты построения линейного тренда с помощью функции ЛИНЕЙН

Итоги, полученные в результате применения функции ЛИНЕЙН следующие:

E2=321,87 – параметр а₁

F2=-497462,09 – параметр а₀

Е3=14,6 – стандартная ошибка параметр а₁

F3=424174,55 – стандартная ошибка параметр а₀

Е4=0,88 – коэффициент детерминации R²

F4=3288424,58 – стандартная ошибка модели

Е5=502,51 – фактическое значение F-статистики Фишера

F5=69,00 – число степеней свободы

Е6=5,43E+15 – регрессионная сумма квадратов

F6=7,46E+14 – остаточная сумма квадратов

Исходя из полученных данных, имеем следующую парную линейную регрессию.

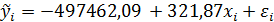
Получаем, что при росте среднегодовой численности работников организаций на 1 человека, инвестиции в среднем увеличатся на 321,87 тыс. рублей.

Задание для самостоятельного выполнения

1. Используя данные представленные в приложении 2.1, необходимо оценить значение парного линейного коэффициента корреляции. Дать интерпретацию полученному значению коэффициента согласно шкалы Чеддока.

2. Используя данные приложения 2.1, необходимо рассчитать параметры парного линейного уравнения регрессии. Пронтерпретировать значения параметра при независимой переменной.

3. Оформить отчет по лабораторной работе.

Тесты

1. Для нахождения параметров множественного регрессионного уравнения (А), при условии, что известны значения независимых переменных (X_j) и результатирующей переменной (Y) необходимо использовать следующую формулу:

- А = (X^TX)^-1X^TY;

- А = (XX)^-1X^TY;

- А = (X^TX)X^TY;

- Нет правильного ответа.

2. Если эконометрическая модель содержит только одну объясняющую переменную и одну объясняемую, то она называется:

- парной линейной регрессией

- парной регрессией

- парной нелинейной регрессией

- множественной линейной регрессией

- множественной регрессией

3. Какая из приведенных ниже формул справедлива?

-

-

-

-

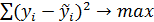
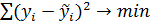
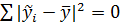
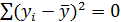
4. Регрессия - это:

- степень взаимосвязи между переменными;

- функциональная зависимость между объясняющими переменными и условным математическим ожиданием зависимой переменной;

- раздел эконометрики.

5. Значение параметра а_j полученное больше нуля указывает на:

- отсутствие связи между показателями y и x;

- обратную связь междупоказателями y и x;

- прямую связь между показателями y и x.

6. Приведенная формула 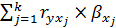является:

- парным линейным коэффициентом корреляции;

- множественным коэффициентом детерминации;

- корреляционным отношением;

- парным коэффициентом детерминации;

- нет правильного ответа.

7. Парный линейный коэффициент корреляции указывает:

- на наличие связи;

- на отсутствие связи;

- на наличие или отсутствие связи и находится в интервале [-1;1];

- на наличие или отсутствие связи и находится в интервале (-1;1);

- нет правильного ответа.

8. Парный линейный коэффициент корреляции принимает значения в интервале:

- от -2 до 0;

- от 0 до 1;

- от -1 до +1.

9. Исследователь получил следующее значение 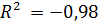. Это указывает на:

- отсутствие зависимость между показателями;

- обратную зависимость между показателями;

- прямую зависимость между показателями;

- ошибку в расчетах.

10. Предложенная формула 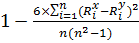является:

- парным коэффициентом корреляции;

- коэффициентом корреляции рангов Спирмена;

- коэффициентом детерминации.

Контрольные вопросы

1. В чем отличие между функциональной и корреляционной связью.

2. Назовите задачи прикладного корреляционно-регрессионного анализа.

3. В чем отличие парного коэффициента корреляции от множественного.

4. В каких границах варьирует значение парного и множественного коэффициента корреляции.

5. Назовите градации шкалы Чеддока.

6. Уравнение регрессии, его смысл и назначение.

7. Сущность метода наименьших квадратов.

Приложение 2.1

	для всех	Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5
Y	X1	X2	X3	X4	X5
Абдулинский			92,5
Адамовский		124,5
Акбулакский		174,3	618,8		88,9
Александровский		150,3	682,2
Асекеевский					14,3
Беляевский		255,1	416,4
Бугурусланский		131,4	633,4
Бузулукский		249,5	763,8		12,5
Гайский		517,4	289,9
Грачевский		50,2	493,4		66,7
Домбаровский		1355,9	491,5
Илекский		65,8			66,7
Кваркенский		555,3	665,8
Красногвардейский		40,2	816,1
Кувандыкский		170,5	170,5
Курманаевский		1605,1	526,3
Матвеевский		27,5	405,6
Новоорский		19831,5	1059,6		27,3
Новосергиевский		2483,4	1824,3		26,9
Октябрьский		86,4	850,5		12,5
Оренбургский		5530,6	4333,5		49,2
Первомайский		304,1	786,9		41,7
Переволоцкий		558,9	1137,5		45,5
Пономаревский		30,2	421,5
Сакмарский		81,2	900,6		36,4
Саракташский		393,7	1593,7		35,3
Светлинский		3787,5
Северный		231,5	882,9
Соль-Илецкий		16,6
Сорочинский		59,1	163,1
Ташлинский		1401,4	636,3
Тоцкий		65,7	933,3
Тюльганский		368,8	715,2		33,3
Шарлыкский		103,9	683,5
Ясненский		207,5	26,5
г.Абдулино		892,5	1628,4
г.Бугуруслан			5000,2		54,5
г.Бузулук			10132,9		19,6
г.Гай		19727,7	2421,2
г.Кувандык
г.Медногорск		4464,1	1697,8
г.Новотроицк		65366,6	7125,4		51,7
г.Оренбург					29,1
г.Орск		32410,8	28902,3		26,1
г.Соль-Илецк		1859,6	2340,7
г.Сорочинск		1727,8	2357,5
г.Ясный		4686,1	1290,1		28,6

Примечание: Y - инвестиции в основной капитал, тыс. руб.

X1 - объем отгруженных товаров собственного производства, выполненных работ и услуг собственными силами, млн. руб.

X2 - оборот розничной торговли, млн. руб.

X3 - объем платных услуг населению , тыс. руб.

X4 - удельный вес убыточных организаций, %

X5 - среднемесячная номинальная начисленная заработная плата работников организаций, руб.