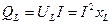Коло синусоїдного струму з індуктивністю.
Коло, яке по відношенню до джерела змінного струму має практично індуктивний характер навантаження можна надати у вигляді котушки, що виконана з мідного проводу великого перерізу. Активний опір витків проводу у такої котушки буде дуже малий і на практиці його величиною можна знехтувати. Котушку, активний опір витків якої нескінченно малий, називають індуктивністю або ідеальною котушкою.
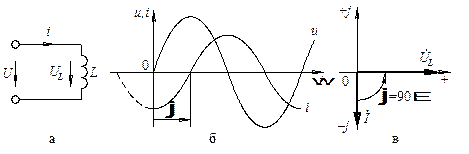
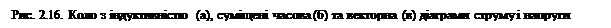
Розглянемо електричне коло (рис. 2.16, а), в якому індуктивність L підключена до джерела синусоїдного струму:
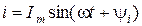 .
.
При проходженні синусоїдного струму в витках котушки генерується ЕРС самоіндукції –
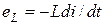 ,
,
яка за величиною дорівнює напрузі uL, що прикладена до котушки, але має протилежний напрямок (uL =- eL).
Після підстановки значення i у вираз ЕРС і диференціювання маємо рівняння розрахунку спаду напруги на індуктивності:
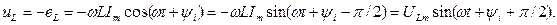
Розділивши обидві частини виразу амплітудного значення спаду напруги на індуктивності (ULm = - wLIm) на 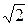 , одержимо рівняння діючих значеннях UL = - wLI і, далі, після перетворень, закон Ома для кола (ділянки кола) з індуктивністю:
, одержимо рівняння діючих значеннях UL = - wLI і, далі, після перетворень, закон Ома для кола (ділянки кола) з індуктивністю:
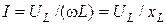 ,
,
де xL = wL = 2pfL – реактивний опір індуктивності, або індуктивний опір, який враховує реакцію кола на зміну магнітного потоку в індуктивності.
Для кола (ділянки кола) з індуктивністю закон Ома у комплексній формі буде:
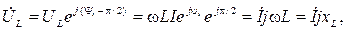
тобто –
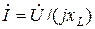 .
.
З аналізу рівняння розрахунку спаду напруги на індуктивності випливає, що вона, подібно до струму кола, змінюється за синусоїдним законом. Так як синусоїди напруги на індуктивності струму кола мають початкові фази, відповідно, yu = yi + p/2та yi, то кут зсуву фаз між ними буде:
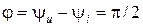 .
.
В загальному випадку суміщені часова та векторна діаграми струму і напруги кола (ділянки кола) з індуктивністю мають вигляд, як на рис. 2.16, б та рис. 2.16, в. При побудові цих діаграм прийнято, що yu = 0°.
Миттєву потужність кола з індуктивністю визначають так:
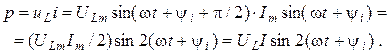
З аналізу виразу розрахунку p випливає, що потужність кола (ділянки кола) з індуктивністю змінюється за синусоїдою, яка має частоту вдвічі більшу ніж частота синусоїд струму або напруги.
З графіка p = f(t)(рис. 2.17) видно, що протягом першої чверті періоду синусоїди струму енергія (WL = LIm2/2), що надходить з мережі, витрачається на утворення магнітного поля котушки. У другій чверті періоду, енергія, яка накопичена в індуктивному елементі, віддається у мережу. Таким чином, відбувається безперервний періодичний процес обміну енергії між індуктивністю і мережею. Цей обмін відбувається без втрат енергії і тому середнє значення потужності кола (ділянки кола) з індуктивністю за період буде –
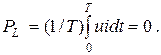
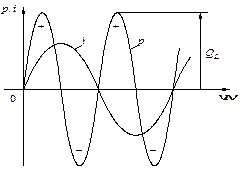
Потужність, яка без втрат коливається між джерелом і індуктивністю називають реактивною індуктивною потужністю QL, вар (вольт ампер реактивний). Її визначають за формулою: