Завдання з теми «Лінійна та векторна алгебри. Елементи аналітичної геометрії».
Зміст
1. Вступ………………………………………………...……………4
2. Завдання для самостійної роботи……………………………….4
2.1. Завдання з теми «Лінійна та векторна алгебри.
Елементи аналітичної геометрії»…………………………..4
2.2. Завдання з теми «Диференціальне числення
функції однієї змінної»…………………………………….11
2.3. Завдання з теми «Невизначений та визначений
інтеграли»……………………………………………..……21
2.4. Завдання з теми «Диференціальні рівняння та
системи»……………………………………………...……..32
2.5. Завдання з теми «Ряди»……………………………………39
3. Зразки виконання завдань…………………………………..….47
3.1. Розв’язання завдань з теми «Лінійна та векторна
алгебри. Елементи аналітичної геометрії»…………….....47
3.2. Розв’язання завдань з теми «Диференціальне
числення функції однієї змінної»………………….….…56
3.3. Розв’язання завдань з теми «Невизначений та
визначений інтеграли»………………...…………..………64
3.4. Розв’язання завдань з теми «Диференціальні
рівняння та системи»…………………………………..…..73
3.5. Розв’язання завдань з теми «Ряди»………………….……84
Література…………………………………………………….…….90
Вступ.
Основною формою навчання студента є систематична самостійна робота над учбовим матеріалом. Лекції, практичні заняття та консультації, заплановані учбовим планом, призначені допомогти студентам в самостійній роботі.
Методичні вказівки містять завдання для самостійної роботи з тем «Лінійна та векторна алгебри. Елементи аналітичної геометрії», «Диференціальне числення функції однієї змінної», «Невизначений та визначений інтеграли», «Диференціальні рівняння та системи», «Ряди». До кожної теми наведені зразки виконання завдань.
2. Завдання для самостійної роботи.
Завдання з теми «Лінійна та векторна алгебри. Елементи аналітичної геометрії».
Рекомендована література:
[1], гл. I-II, III-IV;
[3], гл. I, II, III;
[5], гл. 1-5;
[10], ч. I, III;
[7], ч. I, § 4, 5; ч. II.
Завдання 1.
Задано матриці 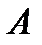 і
і 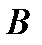 .
.
1. Обчислити матриці 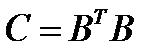 ,
, 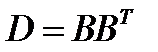 ,
, 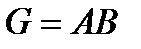 ,
, 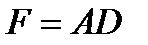 .
.
2. Записати матричне рівняння 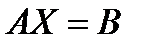 , де
, де 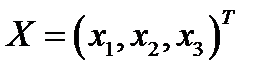 , у вигляді системи лінійних рівнянь.
, у вигляді системи лінійних рівнянь.
3. Розв’язати систему:
а) матричним методом;
б) за формулами Крамера;
в) методом Гаусса.
1. 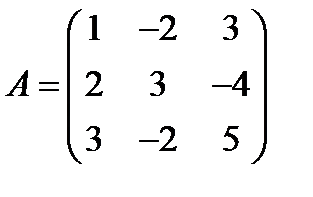 ,
, 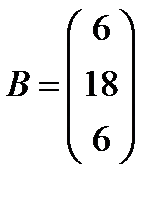 ; 16.
; 16. 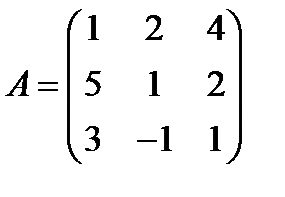 ,
, 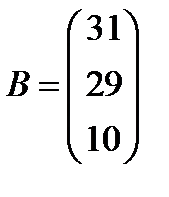 ;
;
2. 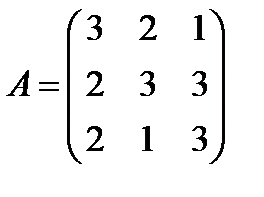 ,
, 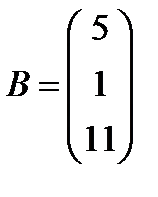 ; 17.
; 17. 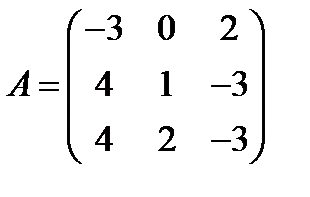 ,
, 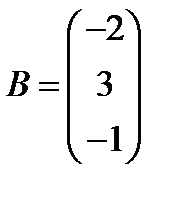 ;
;
3. 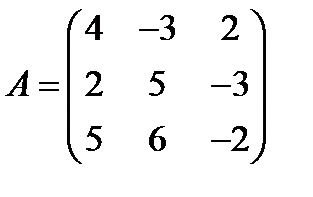 ,
, 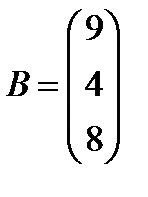 ; 18.
; 18. 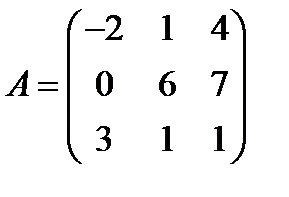 ,
, 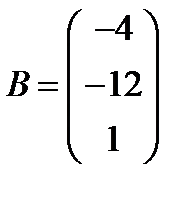 ;
;
4. 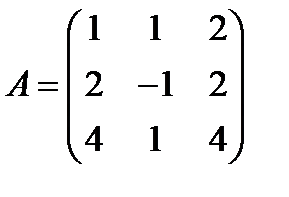 ,
, 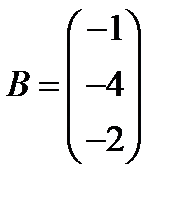 ; 19.
; 19. 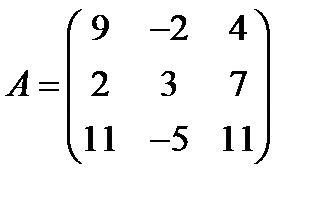 ,
, 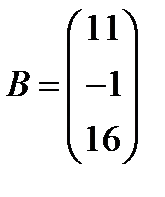 ;
;
5. 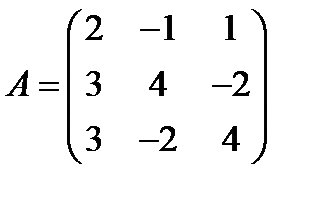 ,
, 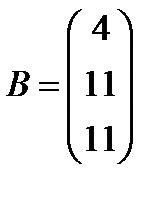 ; 20.
; 20. 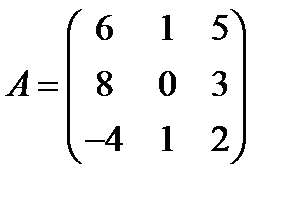 ,
, 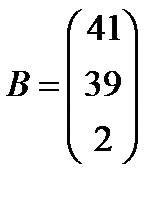 ;
;
6. 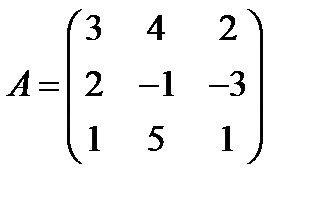 ,
, 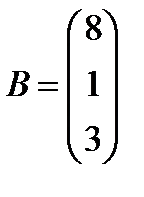 ; 21.
; 21. 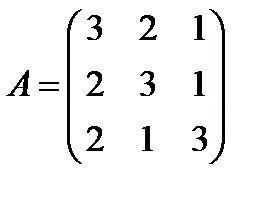 ,
, 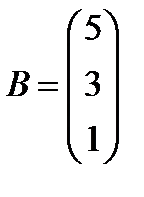 ;
;
7. 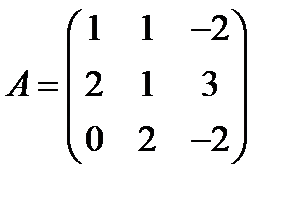 ,
, 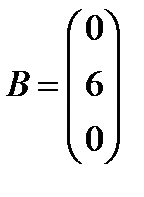 ; 22.
; 22. 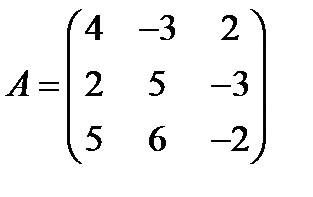 ,
, 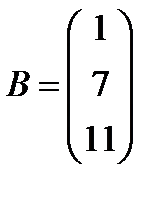 ;
;
8. 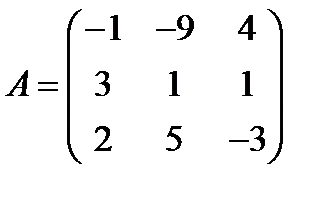 ,
, 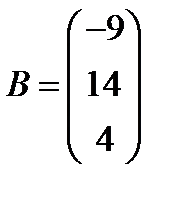 ; 23.
; 23. 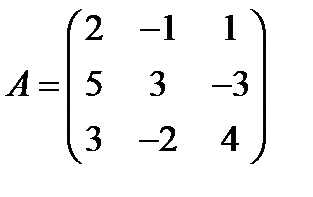 ,
, 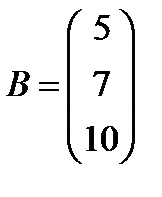 ;
;
9. 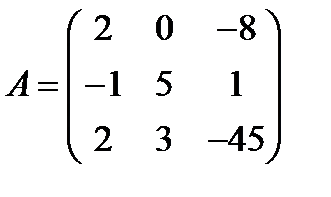 ,
, 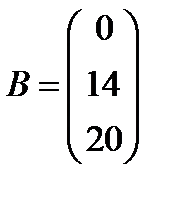 ; 24.
; 24. 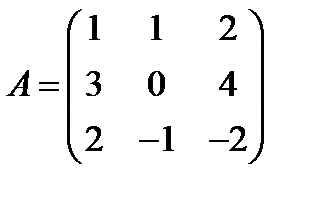 ,
, 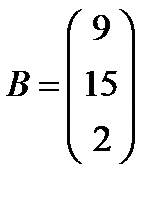 ;
;
10. 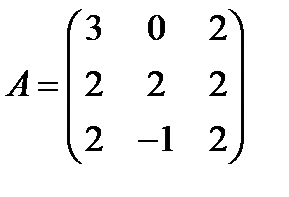 ,
, 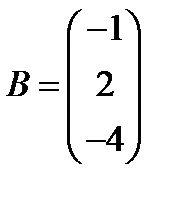 ; 25.
; 25. 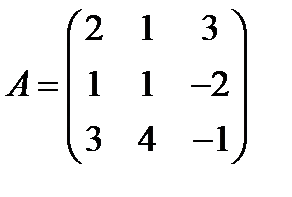 ,
, 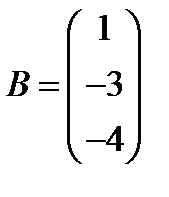 ;
;
11. 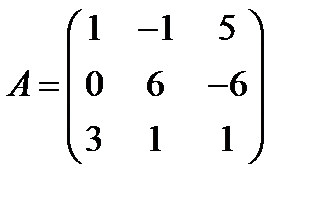 ,
, 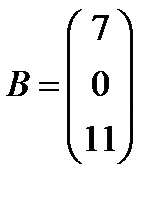 ; 26.
; 26. 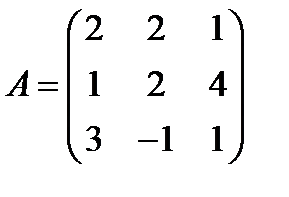 ,
, 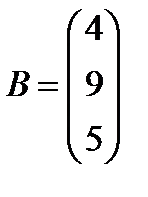 ;
;
12. 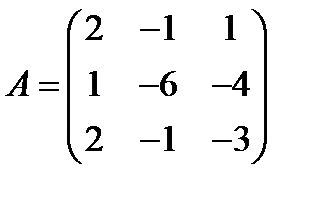 ,
, 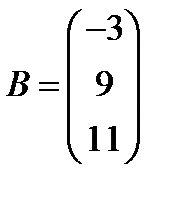 ; 27.
; 27. 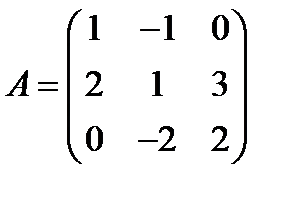 ,
, 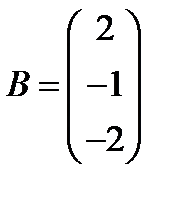 ;
;
13. 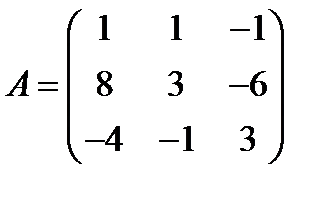 ,
, 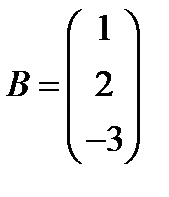 ; 28.
; 28. 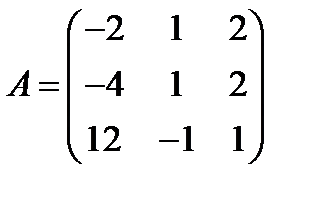 ,
, 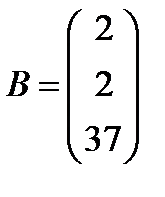 ;
;
14. 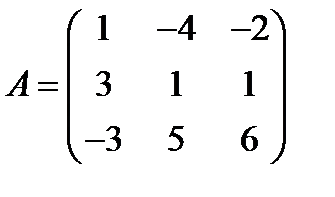 ,
, 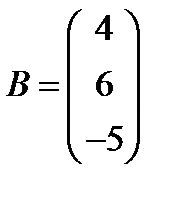 ; 29.
; 29. 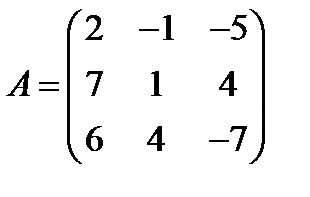 ,
, 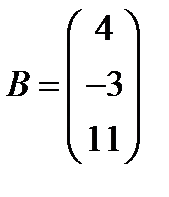 ;
;
15. 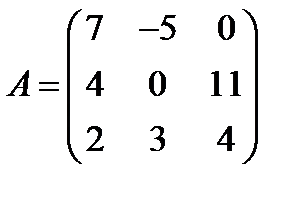 ,
, 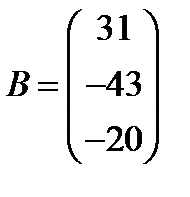 ; 30.
; 30. 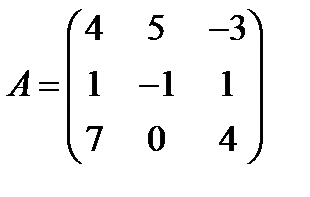 ,
, 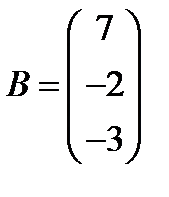 .
.
Завдання 2.
Задано вектори 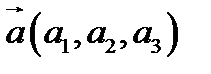 ,
, 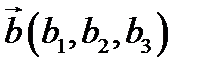 ,
, 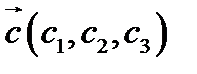 і
і 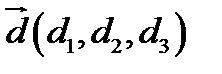 в деякому базисі. Показати, що вектори
в деякому базисі. Показати, що вектори 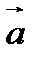 ,
, 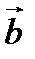 ,
, 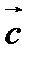 утворюють базис і знайти координати вектора
утворюють базис і знайти координати вектора 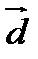 в цьому базисі.
в цьому базисі.
1. 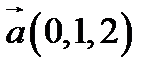 ,
, 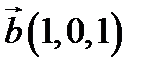 ,
, 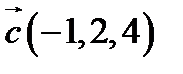 ,
, 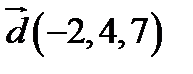 ;
;
2. 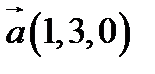 ,
, 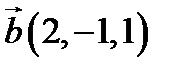 ,
, 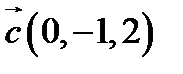 ,
, 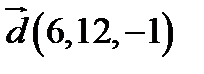 ;
;
3. 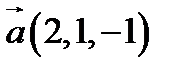 ,
, 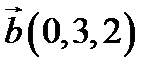 ,
, 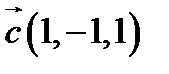 ,
, 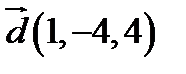 ;
;
4. 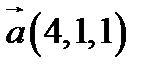 ,
, 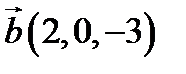 ,
, 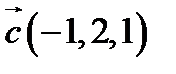 ,
, 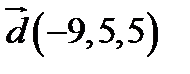 ;
;
5. 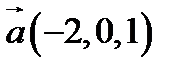 ,
, 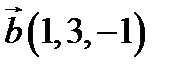 ,
, 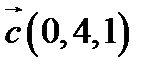 ,
, 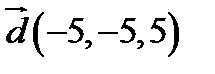 ;
;
6. 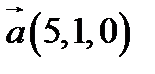 ,
, 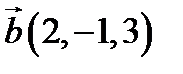 ,
, 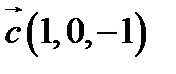 ,
, 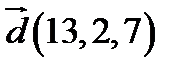 ;
;
7. 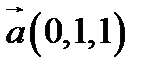 ,
, 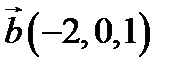 ,
, 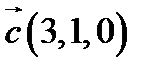 ,
, 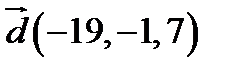 ;
;
8. 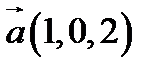 ,
, 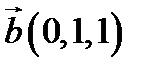 ,
, 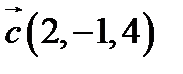 ,
, 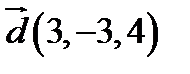 ;
;
9. 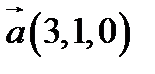 ,
, 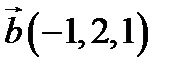 ,
, 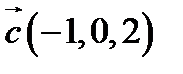 ,
, 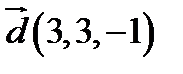 ;
;
10. 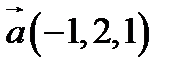 ,
, 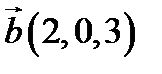 ,
, 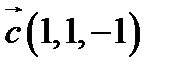 ,
, 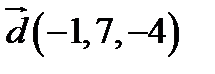 ;
;
11. 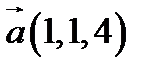 ,
, 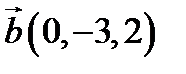 ,
, 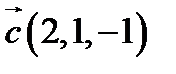 ,
, 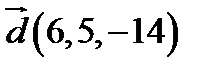 ;
;
12. 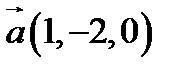 ,
, 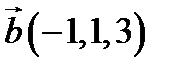 ,
, 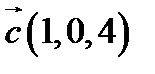 ,
, 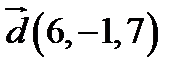 ;
;
13. 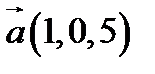 ,
, 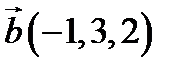 ,
, 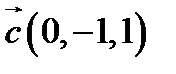 ,
, 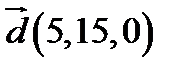 ;
;
14. 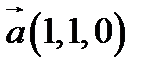 ,
, 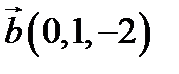 ,
, 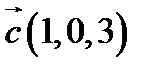 ,
, 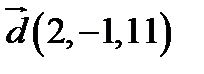 ;
;
15. 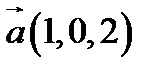 ,
, 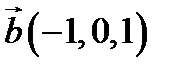 ,
, 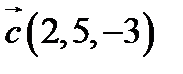 ,
, 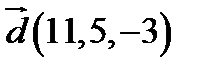 ;
;
16. 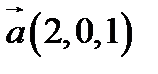 ,
, 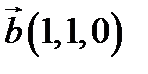 ,
, 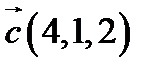 ,
, 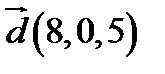 ;
;
17. 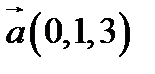 ,
, 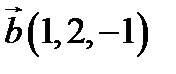 ,
, 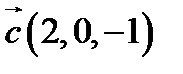 ,
, 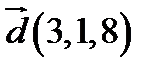 ;
;
18. 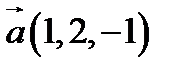 ,
, 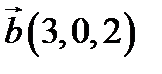 ,
, 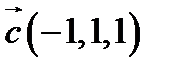 ,
, 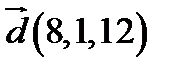 ;
;
19. 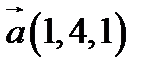 ,
, 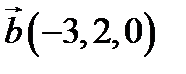 ,
, 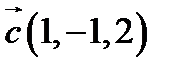 ,
, 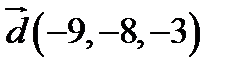 ;
;
20. 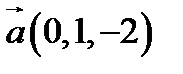 ,
, 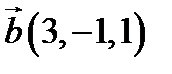 ,
, 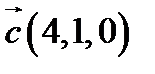 ,
, 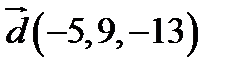 ;
;
21. 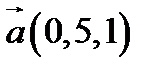 ,
, 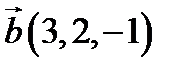 ,
, 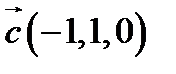 ,
, 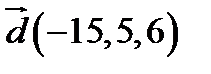 ;
;
22. 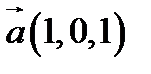 ,
, 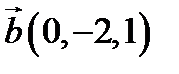 ,
, 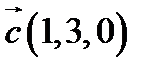 ,
, 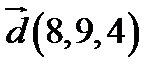 ;
;
23. 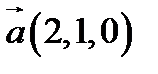 ,
, 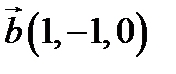 ,
, 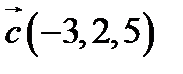 ,
, 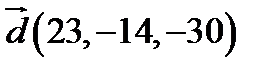 ;
;
24. 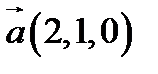 ,
, 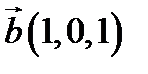 ,
, 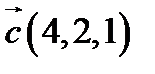 ,
, 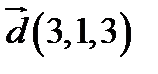 ;
;
25. 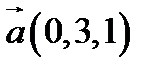 ,
, 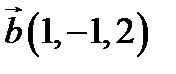 ,
, 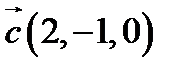 ,
, 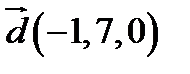 ;
;
26. 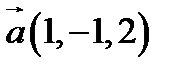 ,
, 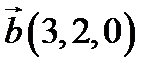 ,
, 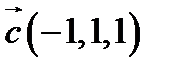 ,
, 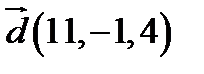 ;
;
27. 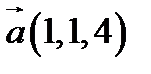 ,
, 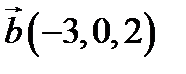 ,
, 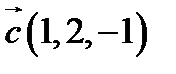 ,
, 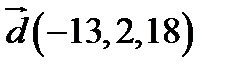 ;
;
28. 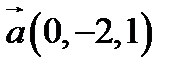 ,
, 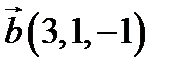 ,
, 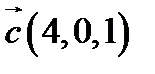 ,
, 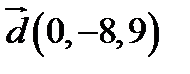 ;
;
29. 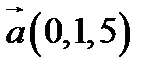 ,
, 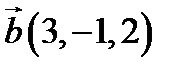 ,
, 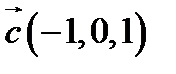 ,
, 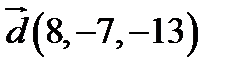 ;
;
30. 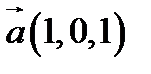 ,
, 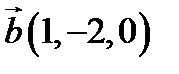 ,
, 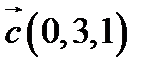 ,
, 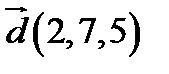 .
.
Завдання 3.
Задано координати вершин піраміди 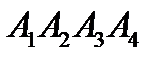 .
.
Знайти: 1) кут між ребром 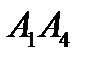 та гранню
та гранню 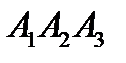 ;
;
2) площу грані 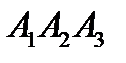 ; 3) об’єм піраміди;
; 3) об’єм піраміди;
4) рівняння висоти, яку проведено з вершини 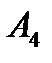 до грані
до грані 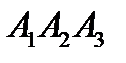 .
.
1. 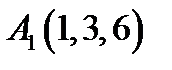 ,
, 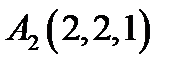 ,
, 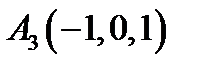 ,
, 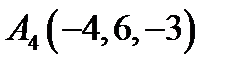 ;
;
2. 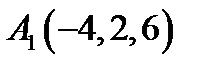 ,
, 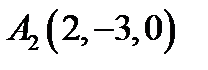 ,
, 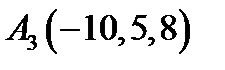 ,
, 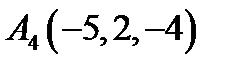 ;
;
3. 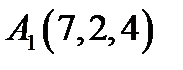 ,
, 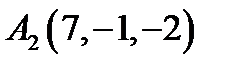 ,
, 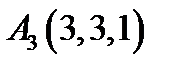 ,
, 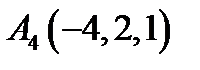 ;
;
4. 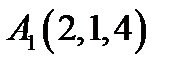 ,
, 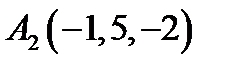 ,
, 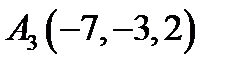 ,
, 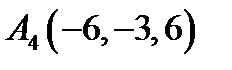 ;
;
5. 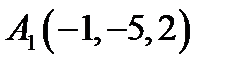 ,
, 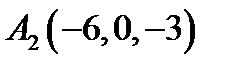 ,
, 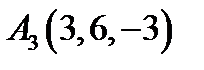 ,
, 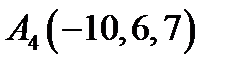 ;
;
6. 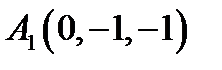 ,
, 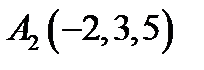 ,
, 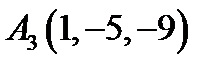 ,
, 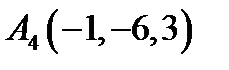 ;
;
7. 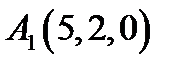 ,
, 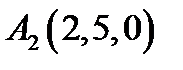 ,
, 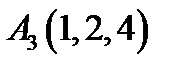 .
. 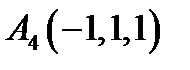 ;
;
8. 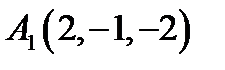 ,
, 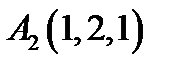 ,
, 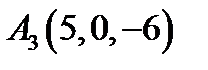 ,
, 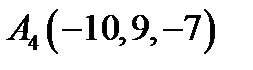 ;
;
9. 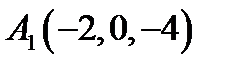 ,
, 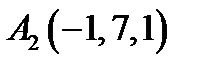 ,
, 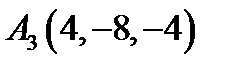 .
. 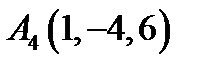 ;
;
10. 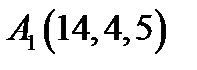 ,
, 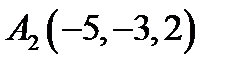 ,
, 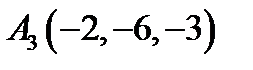 ,
, 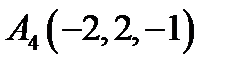 ;
;
11. 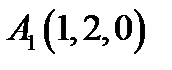 ,
, 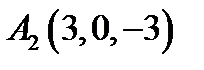 ,
, 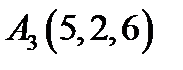 ,
, 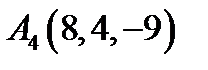 ;
;
12. 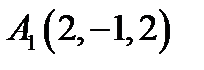 ,
, 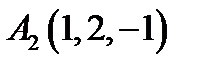 ,
, 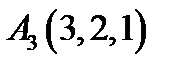 ,
, 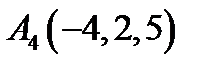 ;
;
13. 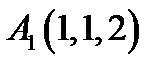 ,
, 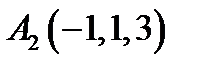 ,
, 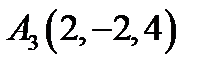 ,
, 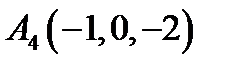 ;
;
14. 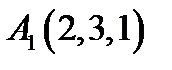 ,
, 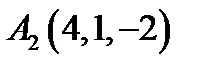 ,
, 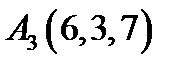 ,
, 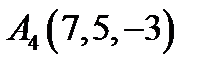 ;
;
15. 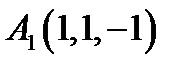 ,
, 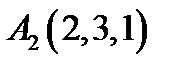 ,
, 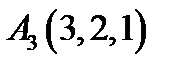 ,
, 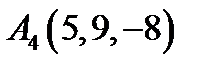 ;
;
16. 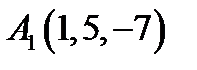 ,
, 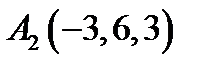 ,
, 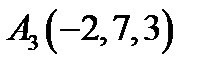 ,
, 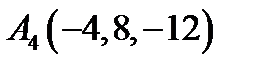 ;
;
17. 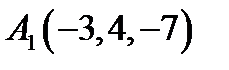 ,
, 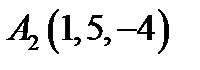 ,
, 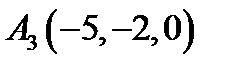 ,
, 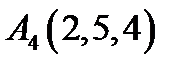 ;
;
18. 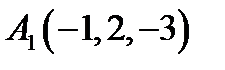 ,
, 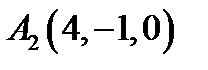 ,
, 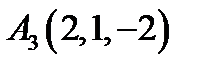 ,
, 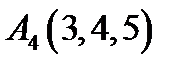 ;
;
19. 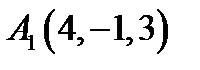 ,
, 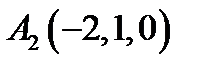 ,
, 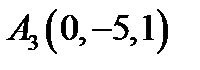 ,
, 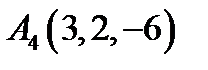 ;
;
20. 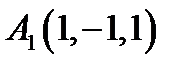 ,
, 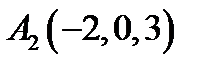 ,
, 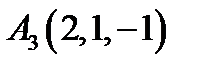 ,
, 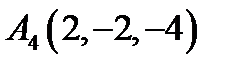 ;
;
21. 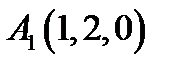 ,
, 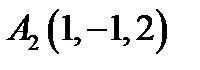 ,
, 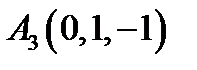 ,
, 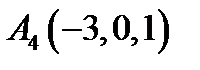 ;
;
22. 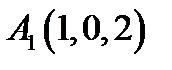 ,
, 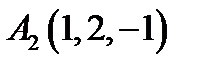 ,
, 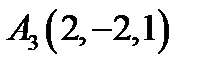 ,
, 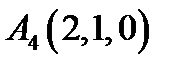 ;
;
23. 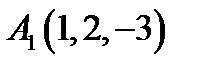 ,
, 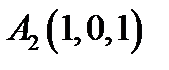 ,
, 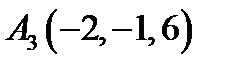 ,
, 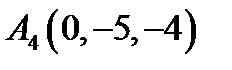 ;
;
24. 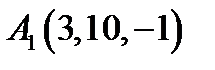 ,
, 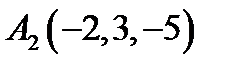 ,
, 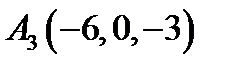 ,
, 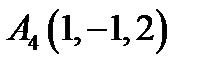 ;
;
25. 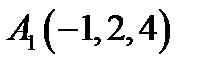 ,
, 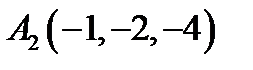 .
. 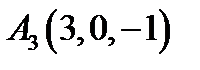 ,
, 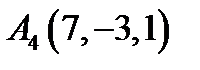 ;
;
26. 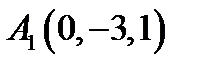 ,
, 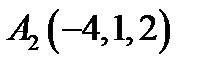 ,
, 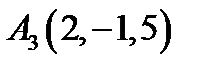 ,
, 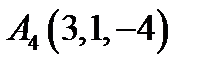 ;
;
27. 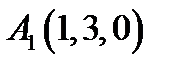 ,
, 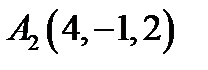 ,
, 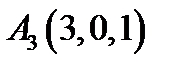 ,
, 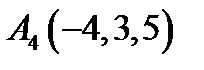 ;
;
28. 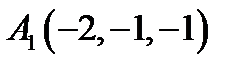 ,
, 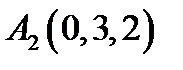 ,
, 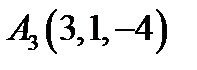 ,
, 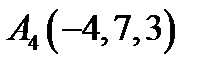 ;
;
29. 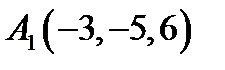 ,
, 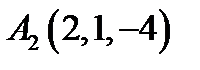 ,
, 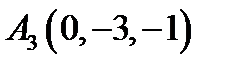 ,
, 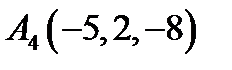 ;
;
30. 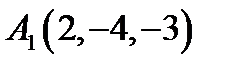 ,
, 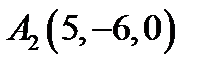 ,
, 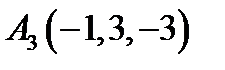 ,
, 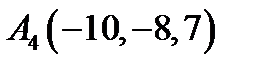 .
.
Завдання 4.
1. Скласти рівняння лінії, для якої відстані кожної точки від початку координат і від точки 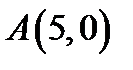 відносяться як
відносяться як 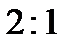 .
.
2. Скласти рівняння лінії, для якої відстань кожної точки від точки 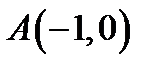 вдвоє менша відстані її від прямої
вдвоє менша відстані її від прямої 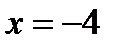 .
.
3. Скласти рівняння лінії, для якої відстані кожної точки від точки 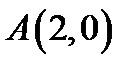 і від прямої
і від прямої 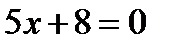 відносяться як
відносяться як 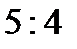 .
.
4. Скласти рівняння лінії, для якої відстань кожної точки від точки 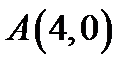 вдвоє більша, ніж від точки
вдвоє більша, ніж від точки 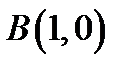 .
.
5. Скласти рівняння лінії, для якої відстані кожної точки від точки 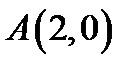 і від прямої
і від прямої 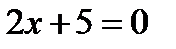 відносяться як
відносяться як 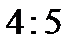 .
.
6. Скласти рівняння лінії, для якої відстань кожної точки від точки 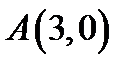 вдвоє менша відстані від точки
вдвоє менша відстані від точки 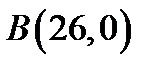 .
.
7. Скласти рівняння лінії, кожна точка якої рівновіддалена від точки 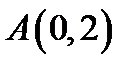 і від прямої
і від прямої 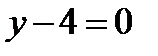 .
.
8. Скласти рівняння лінії, кожна точка якої рівновіддалена від осі ординат і від кола 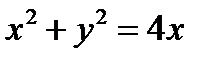 .
.
Зауваження. За відстань від точки 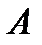 до фігури
до фігури 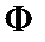 приймається найменша з відстаней між точкою
приймається найменша з відстаней між точкою 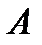 і точками фігури
і точками фігури 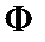 .
.
9. Скласти рівняння лінії, кожна точка якої рівновіддалена від точки 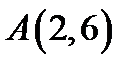 і від прямої
і від прямої 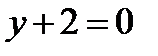 .
.
10. Скласти рівняння лінії, для якої відстань кожної точки від точки 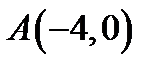 втроє більша, ніж від початку координат.
втроє більша, ніж від початку координат.
11. Визначити траєкторію точки 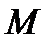 , яка рухається так, що її відстань від точки
, яка рухається так, що її відстань від точки 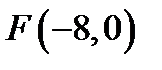 вдвічі більша, ніж від прямої
вдвічі більша, ніж від прямої 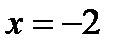 .
.
12. Скласти рівняння геометричного місця точок, які є рівновіддаленими від початку координат і від прямої 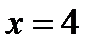 .
.
13. Скласти рівняння множини точок, для яких відстань від точки 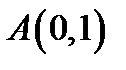 вдвічі менша, ніж від прямої
вдвічі менша, ніж від прямої 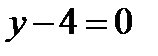 .
.
14. Скласти рівняння лінії, для якої відстані кожної точки від точки 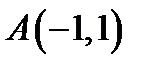 і від прямої
і від прямої 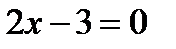 відносяться як
відносяться як 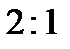 .
.
15. Скласти рівняння геометричного місця точок, для яких сума квадратів відстаней від точок 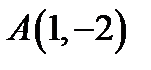 і
і 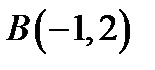 є величина стала і дорівнює 20.
є величина стала і дорівнює 20.
16. Скласти рівняння геометричного місця точок, для яких різниця квадратів відстаней від точок 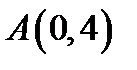 і
і 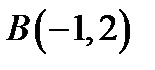 є величина стала і дорівнює 1.
є величина стала і дорівнює 1.
17. Скласти рівняння траєкторії точки 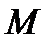 , якщо в кожний момент руху відстань її від точки
, якщо в кожний момент руху відстань її від точки 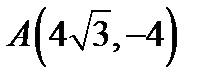 вдвічі більша, ніж від точки
вдвічі більша, ніж від точки 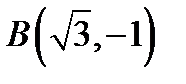 .
.
18. Скласти рівняння множини точок, для яких сума квадратів відстаней від точок 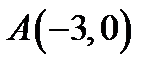 і
і 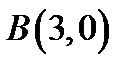 дорівнює 50.
дорівнює 50.
19. Скласти рівняння множини точок, для яких відношення відстаней від точки 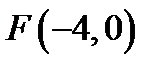 і від прямої
і від прямої 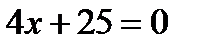 дорівнює
дорівнює 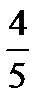 .
.
20. Скласти рівняння множини точок, для яких відношення відстаней від точки 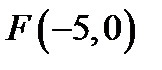 і від прямої
і від прямої 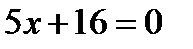 дорівнює
дорівнює 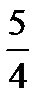 .
.
21. Скласти рівняння геометричного місця точок, які є рівновіддаленими від осі 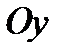 і від точки
і від точки 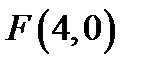 .
.
22. Визначити траєкторію точки 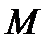 , яка рухається так, що її відстань від точки
, яка рухається так, що її відстань від точки 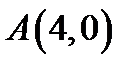 залишається вдвічі меншою, ніж від точки
залишається вдвічі меншою, ніж від точки 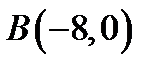 .
.
23. Скласти рівняння геометричного місця точок, для яких сума відстаней від точок 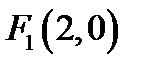 і
і 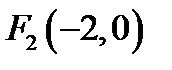 дорівнює
дорівнює 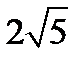 .
.
24. Скласти рівняння геометричного місця точок, для яких різниця відстаней від точок 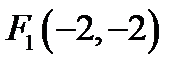 і
і 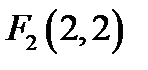 дорівнює 4.
дорівнює 4.
25. Написати рівняння геометричного місця точок, для яких відстань від точки 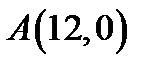 вдвічі більша, ніж від точки
вдвічі більша, ніж від точки 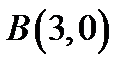 .
.
26. Скласти рівняння геометричного місця точок, які є рівновіддаленими від осі 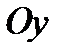 і від точки
і від точки 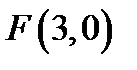 .
.
27. Написати рівняння геометричного місця точок, які є рівновіддаленими від осі 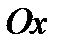 і від точки
і від точки 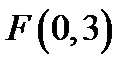 .
.
28. Скласти рівняння геометричного місця точок, які є рівновіддаленими від точки 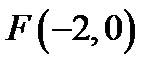 і від прямої
і від прямої 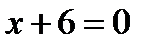 .
.
29. Визначити траєкторію точки 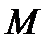 , яка рухається так, що її відстань від точки
, яка рухається так, що її відстань від точки 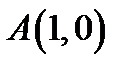 залишається втричі меншою, ніж від прямої
залишається втричі меншою, ніж від прямої 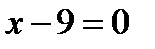 .
.
30. Визначити траєкторію точки 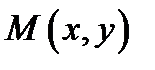 , яка рухається так, що її відстань від прямої
, яка рухається так, що її відстань від прямої 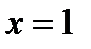 залишається вдвічі меншою, ніж від точки
залишається вдвічі меншою, ніж від точки 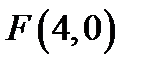 .
.
