Производная и дифференциал 1 страница
Действительные числа
1. Действительные числа и их свойства. Принцип Архимеда.
2. Множество действительных чисел как метрическое пространство. Открытые и замкнутые множества в нем.
Леммы, связанные с полнотой множества действительных чисел:
3. Лемма о вложенных отрезках (принцип Коши - Кантора).
4. Лемма о конечном покрытии (принцип Бореля - Лебега).
5. Лемма о предельной точке (принцип Больцано - Вейерштрасса).
6. Г рани числовых множеств. Теорема существования точных граней.
Предел
7. Предел последовательности. Общие свойства предела.
8. Арифметические свойства сходящихся последовательностей. Предельный переход в неравенствах.
9. Бесконечно малые и бесконечно большие последовательности, их свойства.
10. Критерий сходимости монотонной последовательности. Число е.
11. Подпоследовательности. Теорема Больцано- Вейерштрасса.
12. Верхний и нижний пределы последовательностей.
13. Критерий Коши сходимости последовательностей.
14. Предел функции. Эквивалентность определений Гейне и Коши.
15. Свойства предела функции. Предельный переход и арифметические операции. Предельный переход и неравенства.
16. Предел сложной функции.
17. Предел по базе. Односторонние пределы, пределы на бесконечности.
18. Критерий Коши существования предела функции.
19. Замечательные пределы.
20. Существование предела монотонной функции.
21. Бесконечно малые и бесконечно большие функции. Сравнение асимптотического поведения функций. «О-о» символика.
Непрерывность
22. Непрерывность функции в точке. Точки разрыва, их классификация.
23. Непрерывность сложной функции. Арифметические свойства непрерывных функций.
Свойства функций, непрерывных на отрезке:
24. Теорема Вейерштрасса.
25. Теорема Кольцано - Коши.
26. Критерий непрерывности монотонной функции.
27. Теорема об обратной функции.
28. Равномерная непрерывность. Теорема Кантора.
29. Непрерывность основных элементарных функций.
Производная и дифференциал
30. Производная функции. Связь между существованием производной и непрерывностью.
31. Дифференциал. Необходимые и достаточные условия диффсрснцируемости.
32. Инвариантность формы первого дифференциала.
33. Правила дифференцирования.
34. Производная сложной функции.
35. Производная обратной функции.
36. геометрический смысл производной и дифференциала.
37. Производные основных элементарных функций.
38. Производные высших порядков. Правила вычисления, формула Лейбница.
39. Производные высших порядков от сложных и обратных функций.
40. Дифференцирование параметрически заданных функций.
41. Дифференциалы высших порядков. Нарушение инвариантности формы. Теоремы о среднем:
42. Теорема Ферма.
43. Теорема Ролля.
44. Формула конечных приращений Лагранжа.
45. Теорема Коши.
46. Правило Лопиталя раскрытия неопределенности 0/0.
47. Правило Лопиталя раскрытия неопределенности 8/8.
48. Локальная формула Тейлора. Остаточный член в форме Пеано.
49. Формула Тейлора с остаточным членом в форме Лагранжа и Коши.
50. Основные разложения по формуле Тейлора.
Применение дифференциального исчисления к задачам исследования поведения функций:
51. Условия монотонности функций.
52. Экстремум функции. Необходимое условие экстремума.
53. Достаточное условие экстремума, использующее первую производную.
54. Достаточное условие экстремума, использующее высшие производные.
55. Условия выпуклости и наличия точки перегиба графика функции.
56. Вертикальные и наклонные асимптоты.
17. Односторонние пределы. Пределы на бесконечности. (Гейне): Функция f имеет в точке x0 предел слева (справа), если существует такое число 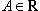 , что для произвольной последовательности (xn) значений x, a < xn < x0 (x0 < xn < b), сходящейся к точке x0 при n → ∞, соответствующая последовательность (f(xn)) значений функции f сходится к точке A. (Коши): Функция f имеет в точке x0 предел слева (справа), если , что для произвольной последовательности (xn) значений x, a < xn < x0 (x0 < xn < b), сходящейся к точке x0 при n → ∞, соответствующая последовательность (f(xn)) значений функции f сходится к точке A. (Коши): Функция f имеет в точке x0 предел слева (справа), если 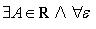 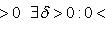 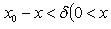 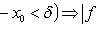 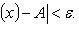 Число A называем пределом слева (справа) функции f в точке x0 и обозначаем f(x0 - 0) (f(x0 + 0)) или Число A называем пределом слева (справа) функции f в точке x0 и обозначаем f(x0 - 0) (f(x0 + 0)) или 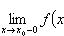 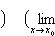 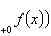 . Функция f имеет предел в точке x0 тогда и только тогда, когда в этой точке существуют и равные между собой пределы слева и справа. Предел функции на бесконечности в математическом анализе описывает поведение значения данной функции, когда её аргумент становится бесконечно большим по модулю. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) – b| < e. Запись этого факта: . Функция f имеет предел в точке x0 тогда и только тогда, когда в этой точке существуют и равные между собой пределы слева и справа. Предел функции на бесконечности в математическом анализе описывает поведение значения данной функции, когда её аргумент становится бесконечно большим по модулю. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) – b| < e. Запись этого факта: 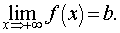 Если область определения данной функции неограниченна снизу, то число b называется пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа e < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство |f(x) – b| < e. Записывается это так: Если область определения данной функции неограниченна снизу, то число b называется пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа e < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство |f(x) – b| < e. Записывается это так: 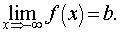 | 18. Критерий Коши существования предела функции. Условие Коши. Будем говорить, что функция f(x) удовлетворяет в точке a условию Коши, если для любого положительного числа e найдется положительное d(e), что для любых x1,x2, удовлетворяющих условию 0<|x1-a|<d, 0<|x2-a|<d, справедливо неравенство |f(x1-f(x2)|<e. Критерий Коши. Для того, чтобы существовал предел функции f(x) в точке a (limx ->af(x) = A ) необходимо и достаточно, чтобы f(x) удовлетворяла в точке a условию Коши. Доказательство Необходимость. Пусть 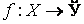 и и 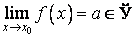 . Это означает, что для любого > 0 существует такое > 0, что для всех точек . Это означает, что для любого > 0 существует такое > 0, что для всех точек 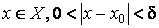 справедливо неравенство справедливо неравенство 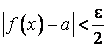 . Достаточность . Достаточность 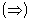 . Теорема об эквивалентности двух определений предела: . Теорема об эквивалентности двух определений предела: 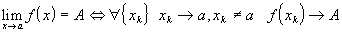 (Определение предела по Гейне-Борелю). Применяем критерий Коши для последовательности. Докажем, что этот предел не зависит от выбора последовательности (Определение предела по Гейне-Борелю). Применяем критерий Коши для последовательности. Докажем, что этот предел не зависит от выбора последовательности 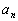 . Для этого рассмотрим другую извлеченную последовательность . Для этого рассмотрим другую извлеченную последовательность 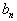 , тоже сходящуюся к a. Соответствующая ей последовательность , тоже сходящуюся к a. Соответствующая ей последовательность 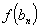 сходится к пределу B. Для доказательства, что A=B, допустим противное. Рассмотрим последовательность: сходится к пределу B. Для доказательства, что A=B, допустим противное. Рассмотрим последовательность: 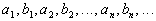 , сходящуюся к a. Последовательность значений функции , сходящуюся к a. Последовательность значений функции 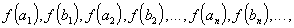 не имеет предела, т.к. ее четные и нечетные члены сходятся к разным пределам A и B соответственно. Таким образом, получилось противоречие. не имеет предела, т.к. ее четные и нечетные члены сходятся к разным пределам A и B соответственно. Таким образом, получилось противоречие. | 19. Замечательные пределы. Первый замечательный предел 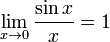 Доказательство Доказательство 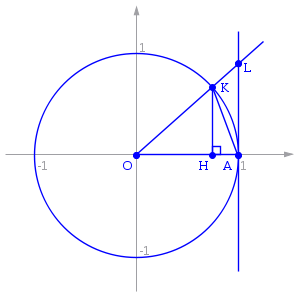 Рассмотрим односторонние пределы Рассмотрим односторонние пределы 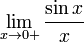 и и 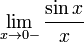 и докажем, что они равны 1. Пусть и докажем, что они равны 1. Пусть 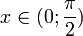 . Отложим этот угол на единичной окружности (R = 1). Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX. Очевидно, что: . Отложим этот угол на единичной окружности (R = 1). Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX. Очевидно, что: 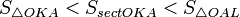 (1) (где SsectOKA — площадь сектора OKA) (1) (где SsectOKA — площадь сектора OKA) 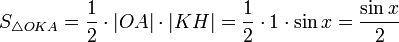 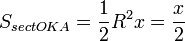 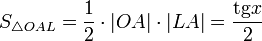 (из (из  : | LA | = tgx) Подставляя в (1), получим: : | LA | = tgx) Подставляя в (1), получим: 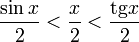 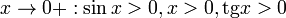 Так как при: Так как при: 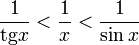 Умножаем на sinx: Умножаем на sinx: 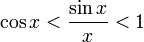 Перейдём к пределу: Перейдём к пределу: 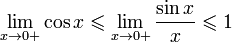 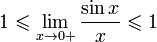 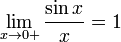 Найдём левый односторонний предел: Найдём левый односторонний предел: 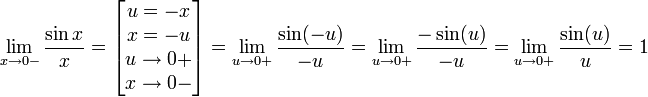 Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1 Второй замечательный предел Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1 Второй замечательный предел 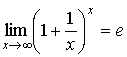 . Доказательство Для любого действительного положительного аргумента можно указать два последовательных натуральных числа, для которых будет выполнено неравенство n < x < n + 1. В том случае имеем n → ∞ ⇒ x → ∞. По свойству для неравенств имеем . Доказательство Для любого действительного положительного аргумента можно указать два последовательных натуральных числа, для которых будет выполнено неравенство n < x < n + 1. В том случае имеем n → ∞ ⇒ x → ∞. По свойству для неравенств имеем 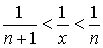 . Прибавим ко всем частям неравенств единицу . Прибавим ко всем частям неравенств единицу 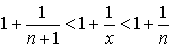 . По свойству степеней имеем . По свойству степеней имеем 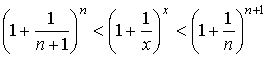 Так как Так как 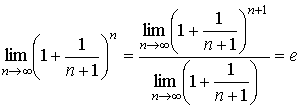 и и 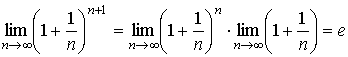 , то по теореме о пределе промежуточной функции имеем также и , то по теореме о пределе промежуточной функции имеем также и 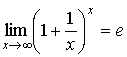 , что и требовалось доказать. Для отрицательного х доказательство аналогично. , что и требовалось доказать. Для отрицательного х доказательство аналогично. | |||
20. Существование предела монотонной функции. Функция 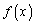 называется - монотонно возрастающей, если из называется - монотонно возрастающей, если из 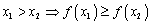 -строго монотонно возрастающей, если из -строго монотонно возрастающей, если из 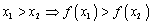 - монотонно убывающей, если из - монотонно убывающей, если из 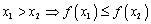 -строго монотонно убывающей, если из -строго монотонно убывающей, если из 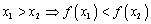 . Если же для любых точек x1ÎX и x2ÎX, x1 < x2, выполняется неравенство f(x1)£f(x2) (соответственно неравенство f(x1) ³ f(x2)), то функцию называют неубывающей (невозрастающей). Иногда удобнее и в этом случае называть функцию возрастающей (убывающей) – но в широком смысле. Возрастающие и убывающие на множестве X функции называются монотонными на этом множестве. Теорема. Пусть функция . Если же для любых точек x1ÎX и x2ÎX, x1 < x2, выполняется неравенство f(x1)£f(x2) (соответственно неравенство f(x1) ³ f(x2)), то функцию называют неубывающей (невозрастающей). Иногда удобнее и в этом случае называть функцию возрастающей (убывающей) – но в широком смысле. Возрастающие и убывающие на множестве X функции называются монотонными на этом множестве. Теорема. Пусть функция 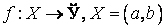 – неубывающая на (a, b), где, в частности, может быть – неубывающая на (a, b), где, в частности, может быть 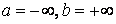 . Если она ограничена сверху числом M, то существует конечный предел . Если она ограничена сверху числом M, то существует конечный предел 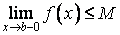 . Если же она не ограничена сверху, то . Если же она не ограничена сверху, то 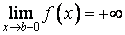 . Аналогично, если функция f ограничена снизу, то в точке a у неё существует конечный предел справа, а если f не ограничена снизу, то . Аналогично, если функция f ограничена снизу, то в точке a у неё существует конечный предел справа, а если f не ограничена снизу, то 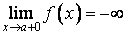 . Подобные утверждения справедливы и для убывающих функций; их можно получить, перейдя от функции f к функции –f. Доказательство. Из ограниченности f следует существование конечной точной верхней грани . Подобные утверждения справедливы и для убывающих функций; их можно получить, перейдя от функции f к функции –f. Доказательство. Из ограниченности f следует существование конечной точной верхней грани 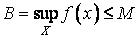 . Таким образом, . Таким образом, 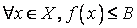 , и для всякого e > 0 существует , и для всякого e > 0 существует 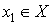 такое, что такое, что 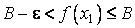 . Но в силу того, что f не убывает, . Но в силу того, что f не убывает, 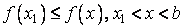 . Таким образом, для любого e>0 можно указать . Таким образом, для любого e>0 можно указать 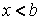 такое, что такое, что 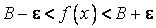 для всех x, удовлетворяющих неравенствам для всех x, удовлетворяющих неравенствам 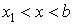 . Это и значит, что . Это и значит, что 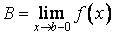 . Пусть теперь неубывающая функция f не ограничена сверху. Тогда для любого M существует . Пусть теперь неубывающая функция f не ограничена сверху. Тогда для любого M существует 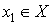 такое, что M < f(x1), и вследствие того, что f не убывает на X, такое, что M < f(x1), и вследствие того, что f не убывает на X, 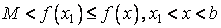 , а это и говорит о том, что , а это и говорит о том, что 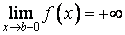 . . | 21. Бесконечно малые и бесконечно большие функции. Сравнение асимптотического поведения функций. «О-о» символика. Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если 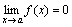 или или 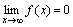 , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю. Примеры. Функция f(x)=(x-1)2 является бесконечно малой при x→1, так как , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю. Примеры. Функция f(x)=(x-1)2 является бесконечно малой при x→1, так как 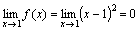 Функция f(x) = tgx – бесконечно малая при x→0. f(x) = ln (1+x)– бесконечно малая при x→0. f(x) = 1/x– бесконечно малая при x→∞. Если для любой последовательности Функция f(x) = tgx – бесконечно малая при x→0. f(x) = ln (1+x)– бесконечно малая при x→0. f(x) = 1/x– бесконечно малая при x→∞. Если для любой последовательности 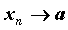 значений аргумента соответствующая последовательность значений функции значений аргумента соответствующая последовательность значений функции 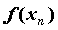 бесконечно большая, то функция бесконечно большая, то функция 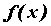 называется бесконечно большой в точке называется бесконечно большой в точке 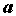 . «O» большое и «o» малое (O и o) — математические обозначения для сравнения асимптотического поведения функций. Пусть f(x) и g(x) — две функции, определенные в некоторой проколотой окрестности точки x0, причем в этой окрестности g не обращается в ноль. Говорят, что: f является «O» большим от g при . «O» большое и «o» малое (O и o) — математические обозначения для сравнения асимптотического поведения функций. Пусть f(x) и g(x) — две функции, определенные в некоторой проколотой окрестности точки x0, причем в этой окрестности g не обращается в ноль. Говорят, что: f является «O» большим от g при 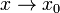 , если существует такая константа C > 0, что для всех x из некоторой окрестности точки x0 имеет место неравенство , если существует такая константа C > 0, что для всех x из некоторой окрестности точки x0 имеет место неравенство 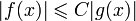 ; f является «о» малым от g при ; f является «о» малым от g при 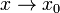 , если для любого ε > 0 найдется такая проколотая окрестность , если для любого ε > 0 найдется такая проколотая окрестность 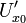 точки x0, что для всех точки x0, что для всех 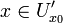 имеет место неравенство имеет место неравенство 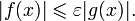 Иначе говоря, в первом случае отношение | f | / | g | в окрестности точки x0 ограничено сверху, а во втором оно стремится к нулю при Иначе говоря, в первом случае отношение | f | / | g | в окрестности точки x0 ограничено сверху, а во втором оно стремится к нулю при 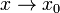 . Сравнение асимптотического поведения функций Определение. Говорят, что функция . Сравнение асимптотического поведения функций Определение. Говорят, что функция 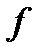 есть бесконечно малая по сравнению с функцией есть бесконечно малая по сравнению с функцией 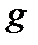 при при 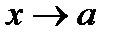 и пишут и пишут 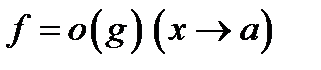 , если , если 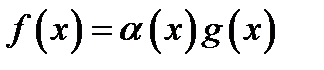 , где , где 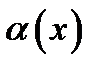 - бесконечно малая функция при - бесконечно малая функция при 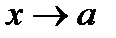 . Замечание. Если функция . Замечание. Если функция 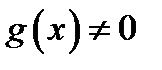 в в 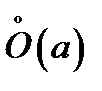 , то последнее определение можно записать как , то последнее определение можно записать как 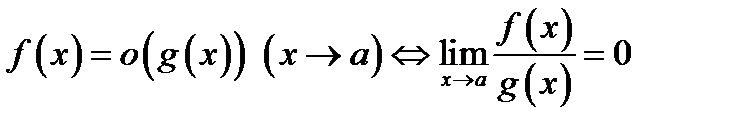 Определение. Говорят, что функции Определение. Говорят, что функции 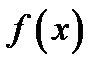 и и 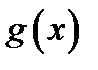 эквивалентны при эквивалентны при 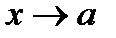 и пишут и пишут 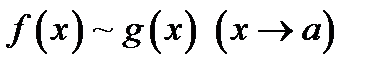 , если , если 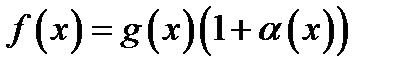 , где , где 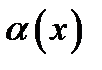 - бесконечно малая функция при - бесконечно малая функция при 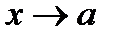 . Замечание. Если . Замечание. Если 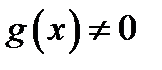 в некоторой в некоторой 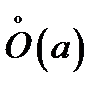 , , 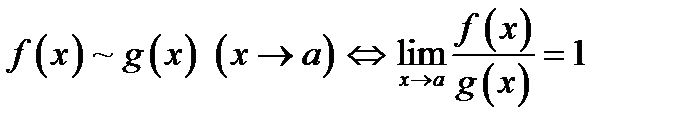 | 22. Непрерывность функции в точке. Точки разрыва, их классификация. Определение 1: Пусть f(x) определена в некоторой окрестности точки а. f(x) называется непрерывной в точке а если 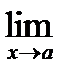 . Определение 2: f(x) называется непрерывной в точке а, если " e > 0 $ d > 0: | f(x) - f(а) | < e при | х - а | < d. f(x) = f(а) Таким образом, можно сказать, что функция непрерывна в точкеx0, если выполнены 3 условия: 1-она определена в точке x0 и в некоторой её окрестности; 2-имеет предел при x → x0; 3-этот предел равен значению функции в точке x0. Предельные точки области определения функции, в которых эта функция не является непрерывной, называются точками её разрыва. Классификация точек разрыва: 1) . Определение 2: f(x) называется непрерывной в точке а, если " e > 0 $ d > 0: | f(x) - f(а) | < e при | х - а | < d. f(x) = f(а) Таким образом, можно сказать, что функция непрерывна в точкеx0, если выполнены 3 условия: 1-она определена в точке x0 и в некоторой её окрестности; 2-имеет предел при x → x0; 3-этот предел равен значению функции в точке x0. Предельные точки области определения функции, в которых эта функция не является непрерывной, называются точками её разрыва. Классификация точек разрыва: 1) 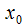 - устранимая т.р. - устранимая т.р. 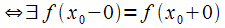 и они конечны, но и они конечны, но 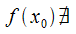 . 2) . 2) 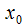 - т.р. 1-го рода: - т.р. 1-го рода: 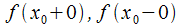 - конечны, но - конечны, но 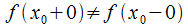 . К примеру, . К примеру, 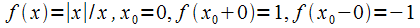 (рис. 8.3). 3) (рис. 8.3). 3) 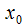 - т.р. 2-го рода: все остальные т.р., например, точки бесконечного разрыва. В частности, - т.р. 2-го рода: все остальные т.р., например, точки бесконечного разрыва. В частности, 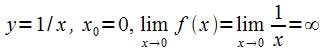 | |||
23. Непрерывность сложной функции. Арифметические свойства непрерывных функций. Пусть аргумент t функции y = f(t) является функцией аргумента x: t = j(x). В этом случае говорят, что переменная у является сложной функцией от аргумента х или у является суперпозицией функций f и j. y = f(j (x)). Пример: y = sin( 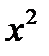 ) - сложная функция. y = sin t, где t = ) - сложная функция. y = sin t, где t = 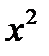 . Если f(x) и g(x) непрерывны в точке а, то f(x) ± g(x), f(x)×g(x) и . Если f(x) и g(x) непрерывны в точке а, то f(x) ± g(x), f(x)×g(x) и 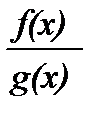 (при условии g(а) ¹ 0) непрерывны в точке а. Доказательство: По условию (при условии g(а) ¹ 0) непрерывны в точке а. Доказательство: По условию 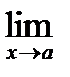 f(x) = f(а), f(x) = f(а), 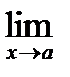 g(x) = g(а) Þ g(x) = g(а) Þ 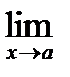 [ f(x) + g(x)] = f(a) + g(а). а это и означает непрерывность суммы функций в точке а. Точно также доказывается непрерывность разности, произведения, частного. Теорема доказана. [ f(x) + g(x)] = f(a) + g(а). а это и означает непрерывность суммы функций в точке а. Точно также доказывается непрерывность разности, произведения, частного. Теорема доказана. | 24. Теорема Вейерштрасса. Первая теорема Вейерштрасса. Пусть 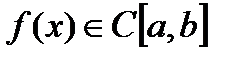 . Тогда . Тогда 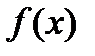 ограничена на ограничена на 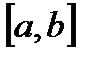 . Доказательство: Докажем, что . Доказательство: Докажем, что 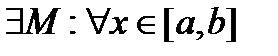 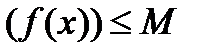 . Предположим противное, то есть . Предположим противное, то есть 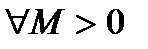 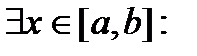 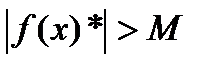 . Возьмем . Возьмем 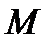 =1,2,3… Получим =1,2,3… Получим 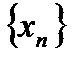 : 1) : 1) 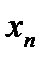 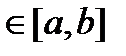 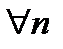 2) 2) 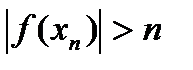 Из этих определений получаем Из этих определений получаем  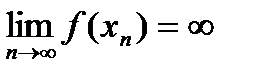 . . 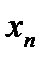 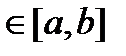 => => 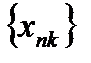 -подпоследовательность последовательности -подпоследовательность последовательности 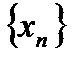 : : 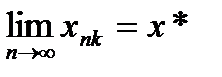 . . 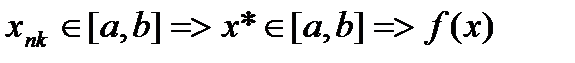 -непрерывна в точке -непрерывна в точке 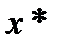 => => 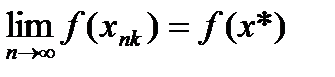 . . 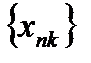 -подпоследовательность последовательности -подпоследовательность последовательности 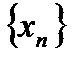 : : 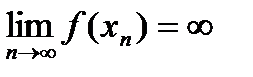 => => 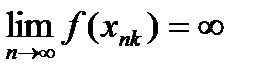 . Противоречие. Вторая теорема Вейерштрасса. Пусть . Противоречие. Вторая теорема Вейерштрасса. Пусть 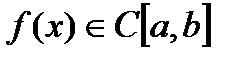 . Тогда . Тогда 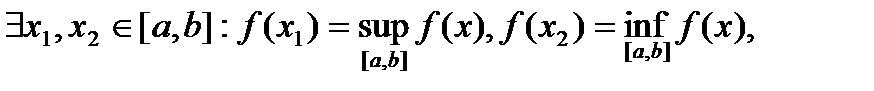 Замечание: Непрерывная на отрезке Замечание: Непрерывная на отрезке 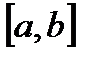 функция на этом отрезке достигает своего наибольшего и наименьшего значения, причем в условиях теоремы отрезок по существу. Доказательство: По условию теоремы функция на этом отрезке достигает своего наибольшего и наименьшего значения, причем в условиях теоремы отрезок по существу. Доказательство: По условию теоремы 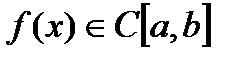 => => 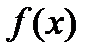 ограничена на ограничена на 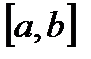 => => 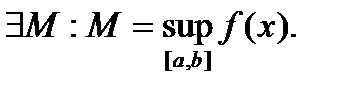 Докажем, что Докажем, что 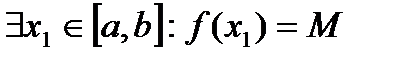 . Предположим противное, то есть . Предположим противное, то есть 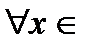 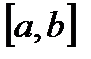 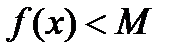 . Рассмотрим вспомогательную функцию . Рассмотрим вспомогательную функцию 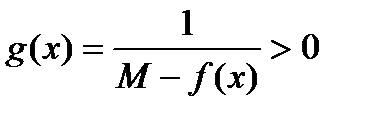 на на 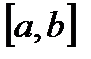 . По 1 теореме Вейерштрасса . По 1 теореме Вейерштрасса 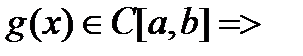 ограничена на ограничена на 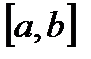 , то есть , то есть 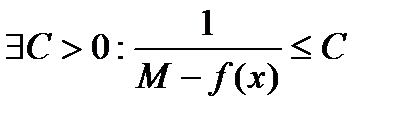 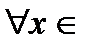 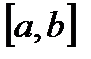 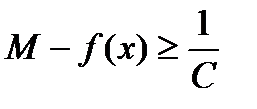 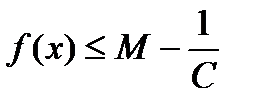 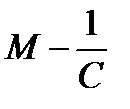 (< (< 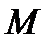 )- верхняя граница. )- верхняя граница. 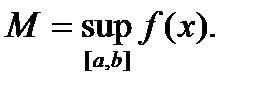 , то есть , то есть 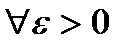 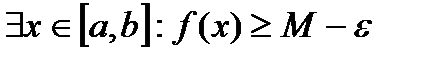 . Противоречие. . Противоречие. | 25. Теорема Больцано-Коши. Пусть дана непрерывная функция на отрезке 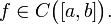 Пусть также Пусть также 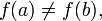 и без ограничения общности предположим, что f(a) = A < B = f(b). Тогда для любого и без ограничения общности предположим, что f(a) = A < B = f(b). Тогда для любого 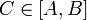 существует существует 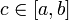 такое, что f(c) = C. Доказательство Рассмотрим функцию такое, что f(c) = C. Доказательство Рассмотрим функцию 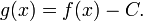 Она непрерывна на отрезке Она непрерывна на отрезке 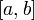 и и 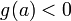 , , 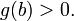 Покажем, что существует такая точка Покажем, что существует такая точка 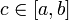 , что , что 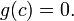 Разделим отрезок Разделим отрезок 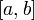 точкой точкой 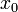 на два равных по длине отрезка, тогда либо на два равных по длине отрезка, тогда либо 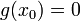 и нужная точка и нужная точка 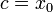 найдена, либо найдена, либо 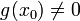 и тогда на концах одного из полученных промежутков функция и тогда на концах одного из полученных промежутков функция 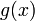 принимает значения разных знаков(на левом конце меньше нуля, на правом больше). Обозначив полученный отрезок принимает значения разных знаков(на левом конце меньше нуля, на правом больше). Обозначив полученный отрезок 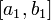 , разделим его снова на два равных по длине отрезка и т.д. Тогда, либо через конечное число шагов придем к искомой точке , разделим его снова на два равных по длине отрезка и т.д. Тогда, либо через конечное число шагов придем к искомой точке  , либо получим последовательность вложенных отрезков , либо получим последовательность вложенных отрезков  по длине стремящихся к нулю и таких, что по длине стремящихся к нулю и таких, что 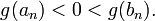 Пусть Пусть  - общая точка всех отрезков - общая точка всех отрезков  , , 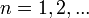 Тогда c = lim an = lim bn, и в силу непрерывности функции Тогда c = lim an = lim bn, и в силу непрерывности функции 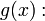 g(c) = lim g(an) = lim g(bn). Поскольку g(c) = lim g(an) = lim g(bn). Поскольку 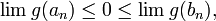 получим, что получим, что 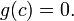 | |||
26. Критерий непрерывности монотонной функции. Для того, чтобы монотонная функция f(x) определенная на [a,b] была непрерывна на [a,b] необходимо и достаточно, чтобы множество значений f(x) заполняло целиком отрезок с концами f(a), f(b) (либо[f(a), f(b)] либо [f(b), f(a)]). Доказательство. Лемма. Для монотонно возрастающей на данном отрезке функции существуют: 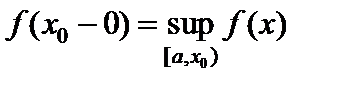 для "x0Î(a,b], и для "x0Î(a,b], и 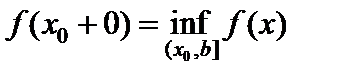 для "x0Î[a,b). Доказательство леммы. Положим для некоторого x0Î(a,b], A= для "x0Î[a,b). Доказательство леммы. Положим для некоторого x0Î(a,b], A= 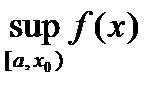 , тогда для "xÎ[a,x0) :f(x)£A и для "e>0$ x¢Î[a,x0):A-e <f(x¢). Так как функция монотонно возрастает, то "xÎ(x¢,x0):A-e < f(x¢) £ f(x)£A. Таким образом, равенство , тогда для "xÎ[a,x0) :f(x)£A и для "e>0$ x¢Î[a,x0):A-e <f(x¢). Так как функция монотонно возрастает, то "xÎ(x¢,x0):A-e < f(x¢) £ f(x)£A. Таким образом, равенство 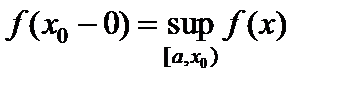 доказано. Аналогично для предела справа доказано. Аналогично для предела справа 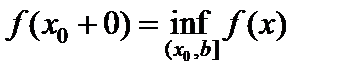 . Для монотонно убывающей функции справедливо аналогичное утверждение. Следствие 1. Монотонно убывающая (возрастающая) на [a,b] функция имеет конечные односторонние пределы. Следствие 2. Монотонно убывающая (возрастающая) на [a,b] функция может иметь там лишь разрывы первого рода. Доказательство критерия. Функцию будем предполагать монотонно возрастающей. Необходимость уже была доказана ранее (пункт 4, следствие 2). Достаточность. Предположим противное. В точке x0 имеется разрыв. Этот разрыв обязан быть разрывом первого рода и, следовательно, должно нарушаться одно из двух соотношений: . Для монотонно убывающей функции справедливо аналогичное утверждение. Следствие 1. Монотонно убывающая (возрастающая) на [a,b] функция имеет конечные односторонние пределы. Следствие 2. Монотонно убывающая (возрастающая) на [a,b] функция может иметь там лишь разрывы первого рода. Доказательство критерия. Функцию будем предполагать монотонно возрастающей. Необходимость уже была доказана ранее (пункт 4, следствие 2). Достаточность. Предположим противное. В точке x0 имеется разрыв. Этот разрыв обязан быть разрывом первого рода и, следовательно, должно нарушаться одно из двух соотношений: 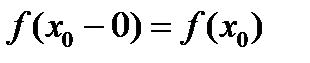 , , 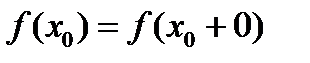 . Пусть, например, . Пусть, например, 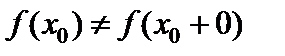 . Так как функция возрастает, то это означает, что . Так как функция возрастает, то это означает, что 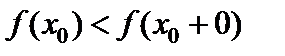 .По лемме .По лемме 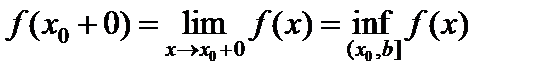 . Имеем . Имеем 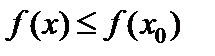 при x £ x0, f(x0) < f(x0+0) £ f(x) при при x £ x0, f(x0) < f(x0+0) £ f(x) при 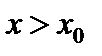 . Таким образом, значения между f(x0), f(x0+0) не достигаются, что противоречит условию теоремы. Аналогично проводится доказательство в случае существования разрыва слева. Замечание. Для монотонно убывающей функции доказательство проводится заменой f на –f. . Таким образом, значения между f(x0), f(x0+0) не достигаются, что противоречит условию теоремы. Аналогично проводится доказательство в случае существования разрыва слева. Замечание. Для монотонно убывающей функции доказательство проводится заменой f на –f. | 27. Теорема об обратной функции. если функция f:X→Y , где Y=f(X), обратима, то для нее существует единственная обратная функция f−1:Y→X и если y=f(x) то x=f−1(y), и если x=f−1(y), то y=f(x) и f−1(f(x))=x при любом x∈X , f−1(f(y))=y при любом y∈Y . Доказательство. Положим для определенности, что функция f возрастающая. Обратимость функции f — очевидное следствие теоремы о корне (Пусть функция f возрастает (или убывает) на промежутке I, число а - любое из значений, принимаемых f на этом промежутке. Тогда уравнение f(x)=a имеет единственный корень на этом промежутке I.) . Поэтому остается доказать, что функция g, обратная к f, возрастает на множестве E(f). Пусть x1 и x2 — произвольные значения из Е (f), такие, что x2> x1. и пусть y1=g(x1), y2=g(x2). По определению обратной функции x1=f(y1) и x2=f(y2). Воспользовавшись тем условием, что f — возрастающая функция, находим, что допущение y1 ≥ y2 приводит к выводу f (y1)≥f(y2), т. е. x1≥ x2. Это противоречит предположению x2> x1. Поэтому y2> y1 , т. е. из условия x2> x1 следует, что g (x2)>g (x1). Именно это и требовалось доказать. | 28, 32. Инвариантность формы первого дифференциала. 28. Равномерная непрерывность. Теорема Кантора. Функция f: X → R называется равномерно-непрерывной на множестве X, если 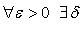 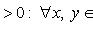 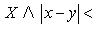 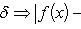 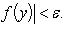 Теорема Кантора Если функция f: [a, b] → R непрерывна на сегменте [a, b], то она равномерно-непрерывна на этом сегменте. 32. Инвариантность формы первого дифференциала. Инвариантность формы первого дифференциала Пусть y = f ( u ( x )) является сложной функцией аргумента x. По определению дифференциала функции имеем df = f '(x)·u '(x)·dx. Так как, в свою очередь, du = u '(x)· dx, то из последнего соотношения получим df = f '(u)·du. Что совпадает с соотношением dy = f '(x)·dx. Форма дифференциала первого порядка сохраняется вне зависимости от того, является ли аргумент независимым или является в свою очередь функцией другого аргумента. Теорема Кантора Если функция f: [a, b] → R непрерывна на сегменте [a, b], то она равномерно-непрерывна на этом сегменте. 32. Инвариантность формы первого дифференциала. Инвариантность формы первого дифференциала Пусть y = f ( u ( x )) является сложной функцией аргумента x. По определению дифференциала функции имеем df = f '(x)·u '(x)·dx. Так как, в свою очередь, du = u '(x)· dx, то из последнего соотношения получим df = f '(u)·du. Что совпадает с соотношением dy = f '(x)·dx. Форма дифференциала первого порядка сохраняется вне зависимости от того, является ли аргумент независимым или является в свою очередь функцией другого аргумента. | |||
29. Непрерывность основных элементарных функций. Все элементарные функции являются непрерывными в любой точке своей области определения. Функция называется элементарной, если она построена из конечного числа композиций и комбинаций (с использованием 4 действий - сложение, вычитание, умножение и деление) основных элементарных функций. Множество основных элементарных функций включает в себя: Алгебраические многочлены 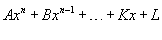 Рациональные дроби Рациональные дроби 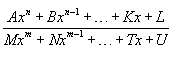 ; Степенные функции ; Степенные функции 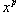 ; Показательные функции ; Показательные функции 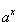 ; Логарифмические функции ; Логарифмические функции 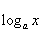 Тригонометрические функции Тригонометрические функции 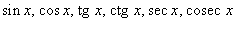 Обратные тригонометрические функции Обратные тригонометрические функции 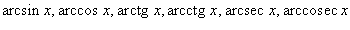 Гиперболические функции Гиперболические функции 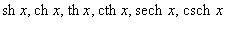  Обратные гиперболические функции Обратные гиперболические функции  | 30. Производная функции. Связь между производной и непрерывностью. Пусть в некоторой окрестности точки 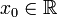 определена функция определена функция 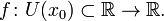 Производной функции называется такое число Производной функции называется такое число 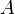 , что функцию в окрестности U(x0) можно представить в виде f(x0 + h) = f(x0) + Ah + o(h) если , что функцию в окрестности U(x0) можно представить в виде f(x0 + h) = f(x0) + Ah + o(h) если 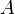 существует. Определение производной функции через предел Пусть в некоторой окрестности точки существует. Определение производной функции через предел Пусть в некоторой окрестности точки 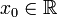 определена функция определена функция 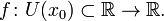 Производной функции f в точке x0 называется предел, если он существует, Производной функции f в точке x0 называется предел, если он существует, 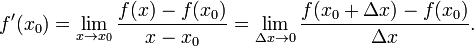 Общепринятые обозначения производной функции y = f(x) в точке x0 Общепринятые обозначения производной функции y = f(x) в точке x0 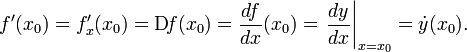 | 31. Дифференциал. Необходимые и достаточные условия дифференцируемости. Дифференциа́л — линейная часть приращения функции. Для функций Дифференциал функции 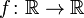 в точке в точке 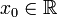 может быть определён как линейная функция может быть определён как линейная функция 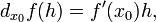 где f'(x0) обозначает производную f в точке x0. Таким образом df есть функция двух аргументов где f'(x0) обозначает производную f в точке x0. Таким образом df есть функция двух аргументов 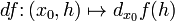 . Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция . Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция 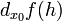 линейно зависящая от h и для которой верно следующее соотношение линейно зависящая от h и для которой верно следующее соотношение 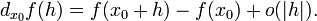 Теорема: Для того, чтобы функция f(x) была дифференцируема в точке x0 необходимо и достаточно, чтобы у нее существовала производная в этой точке. При этом Теорема: Для того, чтобы функция f(x) была дифференцируема в точке x0 необходимо и достаточно, чтобы у нее существовала производная в этой точке. При этом
где α(Δx) - бесконечно малая функция, при Δx→0. Доказательство Т.е. получили, что существует конечная производная функции в точке x0 и y/(x0)=A. Если функция f(x) имеет конечный предел b при Δx→0 , то ее можно представить: f(x)=b+α(x) (α(x)→0) . Исходя из этого: ΔxΔy=y/(x0)+α(Δx), где limΔx→0α(Δx)=0, Δy=y/(x0)·Δx+α(Δx)·Δx→ A=y/(x0) . Теорема доказана. | |||
33. Правила дифференцирования. При дифференцировании константу можно выносить за производную: 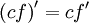 Правило дифференцирования суммы функций: Правило дифференцирования суммы функций: 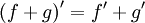 Правило дифференцирования разности функций: Правило дифференцирования разности функций: 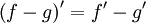 Правило дифференцирования произведения функций (правило Лейбница): Правило дифференцирования произведения функций (правило Лейбница): 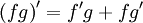 Правило дифференцирования частного функций: Правило дифференцирования частного функций: 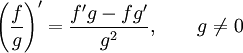 Правило дифференцирования функции в степени другой функции: Правило дифференцирования функции в степени другой функции: 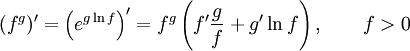 Правило дифференцирования сложной функции: Правило дифференцирования сложной функции: 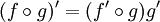 Правило логарифма при дифференцировании функции: Правило логарифма при дифференцировании функции: 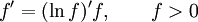 | 34. Производная сложной функции. Если функция u= u(x) имеет в некоторой точке x0 производную 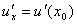 и принимает в этой точке значение u0 = u(x0), а функция y= f(u) имеет в точке u0 производную y 'u= f '(u0), то сложная функция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y 'x= f '(u0)·u '(x0), где вместо u должно быть подставлено выражение u= u(x). Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x. Доказательство. При фиксированном значении х0 будем иметь u0=u(x0), у0=f(u0). Для нового значения аргумента x0+Δx: Δu= u(x0 + Δx) – u(x0), Δy=f(u0+Δu) – f(u0). Т.к. u – дифференцируема в точке x0, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0 Δy→0. По условию и принимает в этой точке значение u0 = u(x0), а функция y= f(u) имеет в точке u0 производную y 'u= f '(u0), то сложная функция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y 'x= f '(u0)·u '(x0), где вместо u должно быть подставлено выражение u= u(x). Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x. Доказательство. При фиксированном значении х0 будем иметь u0=u(x0), у0=f(u0). Для нового значения аргумента x0+Δx: Δu= u(x0 + Δx) – u(x0), Δy=f(u0+Δu) – f(u0). Т.к. u – дифференцируема в точке x0, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0 Δy→0. По условию 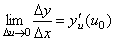 . Из этого соотношения, пользуясь определением предела, получаем (при Δu→0) . Из этого соотношения, пользуясь определением предела, получаем (при Δu→0) 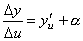 , где α→0 при Δu→0, а, следовательно, и при Δx→0. Перепишем это равенство в виде: Δy= y 'uΔu+α·Δu. Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx , где α→0 при Δu→0, а, следовательно, и при Δx→0. Перепишем это равенство в виде: Δy= y 'uΔu+α·Δu. Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx 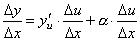 . По условию . По условию 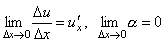 . Поэтому, переходя к пределу при Δx→0, получим y 'x= y 'u·u 'x . Теорема доказана. Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от "внешней" функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от "внутренней" функции по независимой переменной. Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y 'x осуществляется последовательным применением предыдущей теоремы. По доказанному правилу имеем y 'x= y 'u·u 'x . Применяя эту же теорему для u 'x получаем . Поэтому, переходя к пределу при Δx→0, получим y 'x= y 'u·u 'x . Теорема доказана. Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от "внешней" функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от "внутренней" функции по независимой переменной. Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y 'x осуществляется последовательным применением предыдущей теоремы. По доказанному правилу имеем y 'x= y 'u·u 'x . Применяя эту же теорему для u 'x получаем 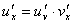 , т.е. y 'x = y 'x· u 'v· v 'x = f 'u (u)·u 'v (v)·v 'x (x). , т.е. y 'x = y 'x· u 'v· v 'x = f 'u (u)·u 'v (v)·v 'x (x). | 35. Производная обратной функции. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у0 имеет производную g '(v0), отличную от нуля, то в соответствующей точке x0=g(x0) функция y=f(x) имеет производную f '(x0), равную 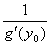 , т.е. справедлива формула , т.е. справедлива формула 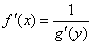 . Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0. Покажем, что . Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0. Покажем, что 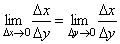 . Пусть . Пусть 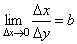 . Тогда по свойству предела . Тогда по свойству предела 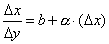 . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е. . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е. 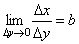 . Следовательно, . Следовательно, 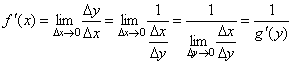 , что и требовалось доказать. Эту формулу можно записать в виде , что и требовалось доказать. Эту формулу можно записать в виде 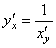 . . |
35. Производная обратной функции. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у0 имеет производную g '(v0), отличную от нуля, то в соответствующей точке x0=g(x0) функция y=f(x) имеет производную f '(x0), равную 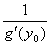 , т.е. справедлива формула , т.е. справедлива формула 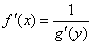 . Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0. Покажем, что . Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0. Покажем, что 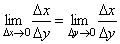 . Пусть . Пусть 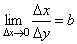 . Тогда по свойству предела . Тогда по свойству предела 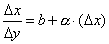 . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е. . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е. 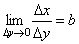 . Следовательно, . Следовательно, 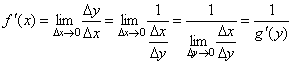 , что и требовалось доказать. Эту формулу можно записать в виде , что и требовалось доказать. Эту формулу можно записать в виде 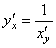 . . | 36. Геометрический смысл производной и дифференциала. Геометрический смысл производной Рассмотрим график функции y = f(x), определенной и непрерывной на (a,b). Зафиксируем произвольную точку x на (a,b), и зададим приращение D x№ 0, причем x+D x О (a,b). Пусть точки M,P - точки на графике f(x), абсциссы которых равны x, x+D x (рис.21). Координаты точек M и P имеют вид M(x,f(x)), P(x+D x,f(x+D x). Прямую, проходящую через точки M, P графика функции f(x) будем называть секущей. Обозначим угол наклона секущей MP к оси ОX через f (D x). Определение 3. Если существует предельное положение секущей MP при стремлении точки N к точке M вдоль графика функции при D x® 0), то это предельное положение называется касательной к графику функции f(x) в данной точке M этого графика. 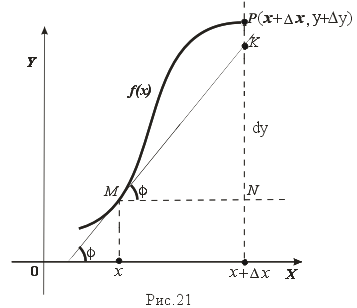 Из данного определения следует, что для существования касательной к графику f(x) в точке M достаточно, чтобы существовал предел limD x® 0f (D x) = f 0, который равен углу, образованному касательной с положительным направлением оси OX. Справедливо утверждение: Предложение 1. Если f(x) имеет в данной точке x производную, то существует касательная к графику функции f(x) в точке M( x,f(x)) , причем угловой коэффициент этой касательной равен производной f'(x). Из этого утверждения вытекает геометрический смысл производной: производная f'(x0) есть угловой коэффициент касательной, проведенной к кривой y = f(x) в точке x0, который в свою очередь равен tg угла наклона касательной к графику функции. Тогда уравнение касательной к кривой f(x) в точке x0 имеет вид Из данного определения следует, что для существования касательной к графику f(x) в точке M достаточно, чтобы существовал предел limD x® 0f (D x) = f 0, который равен углу, образованному касательной с положительным направлением оси OX. Справедливо утверждение: Предложение 1. Если f(x) имеет в данной точке x производную, то существует касательная к графику функции f(x) в точке M( x,f(x)) , причем угловой коэффициент этой касательной равен производной f'(x). Из этого утверждения вытекает геометрический смысл производной: производная f'(x0) есть угловой коэффициент касательной, проведенной к кривой y = f(x) в точке x0, который в свою очередь равен tg угла наклона касательной к графику функции. Тогда уравнение касательной к кривой f(x) в точке x0 имеет вид 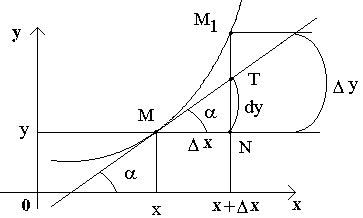 y = f(x0)+f'(x0)(x-x0) ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА Рассмотрим функцию y=f(x) и соответствующую ей кривую. Возьмем на кривой произвольную точку M(x; y), проведем касательную к кривой в этой точке и обозначим через α угол, который касательная образует с положительным направлением оси Ox. Дадим независимой переменной x приращение Δx, тогда функция получит приращение Δy = NM1. Значениям x+Δx и y+Δy на кривой y = f(x) будет соответствовать точка M1(x+Δx; y+Δy). Из ΔMNT находим NT=MN·tg α. Т.к. tg α = f '(x), а MN = Δx, то NT = f '(x)·Δx. Но по определению дифференциала dy=f '(x)·Δx, поэтому dy = NT. Таким образом, дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х. y = f(x0)+f'(x0)(x-x0) ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА Рассмотрим функцию y=f(x) и соответствующую ей кривую. Возьмем на кривой произвольную точку M(x; y), проведем касательную к кривой в этой точке и обозначим через α угол, который касательная образует с положительным направлением оси Ox. Дадим независимой переменной x приращение Δx, тогда функция получит приращение Δy = NM1. Значениям x+Δx и y+Δy на кривой y = f(x) будет соответствовать точка M1(x+Δx; y+Δy). Из ΔMNT находим NT=MN·tg α. Т.к. tg α = f '(x), а MN = Δx, то NT = f '(x)·Δx. Но по определению дифференциала dy=f '(x)·Δx, поэтому dy = NT. Таким образом, дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х. | 37. Производные основных элементарных функций. y = xn. Если n – целое положительное число, то, используя формулу бинома Ньютона: (a + b)n = an+n·an-1·b + 1/2∙n(n – 1)an-2∙b2+ 1/(2∙3)∙n(n – 1)(n – 2)an-3b3+…+ bn, можно доказать, что 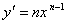 Итак, если x получает приращение Δx, то f(x+Δx) = (x + Δx)n, и, следовательно, Δy=(x+Δx)n – xn =n·xn-1·Δx + 1/2·n·(n–1)·xn-2·Δx2 +…+Δxn. Заметим, что в каждом из пропущенных слагаемых есть множитель Δx в степени выше 3. Найдем предел Итак, если x получает приращение Δx, то f(x+Δx) = (x + Δx)n, и, следовательно, Δy=(x+Δx)n – xn =n·xn-1·Δx + 1/2·n·(n–1)·xn-2·Δx2 +…+Δxn. Заметим, что в каждом из пропущенных слагаемых есть множитель Δx в степени выше 3. Найдем предел 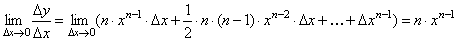 Мы доказали эту формулу для n Î N. Далее увидим, что она справедлива и при любом n Î R. y= sin x. Вновь воспользуемся определением производной. Так как, f(x+Δx)=sin(x+Δx), то Мы доказали эту формулу для n Î N. Далее увидим, что она справедлива и при любом n Î R. y= sin x. Вновь воспользуемся определением производной. Так как, f(x+Δx)=sin(x+Δx), то 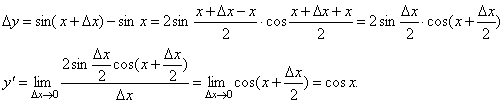 Таким образом, Таким образом, 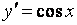 Аналогично можно показать, что Аналогично можно показать, что 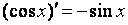 Рассмотрим функцию y= ln x. Имеем f(x+Δx)=ln(x+Δx). Поэтому Рассмотрим функцию y= ln x. Имеем f(x+Δx)=ln(x+Δx). Поэтому 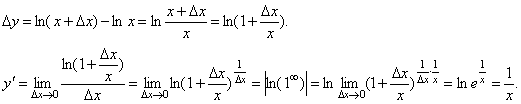 Итак, Итак, 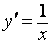 Используя свойства логарифма можно показать, что Используя свойства логарифма можно показать, что 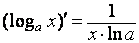 |
