Проверка на статистическую значимость коэффициентов уравнения регрессии и корреляции.

Один из наиболее часто используемых вариантов проверки заключается в следующем. Для полученного уравнения регрессии определяется -статистика - характеристика точности уравнения регрессии, представляющая собой отношение той части дисперсии зависимой переменной которая объяснена уравнением регрессии к необъясненной (остаточной) части дисперсии. Уравнение для определения -статистики в случае многомерной регрессии имеет вид:

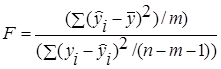
Проверка общего качества уравнения регрессии.

Наиболее часто в практических расчетах для оценки качества всего уравнения в целом применяется коэффициент детерминации , который рассчитывается по формуле

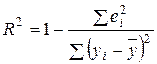
где 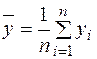. Коэффициент детерминации характеризует долю общего разброса значений зависимой переменной 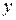, объясненного уравнением регрессии. Считается, что чем больше эта доля, тем лучше уравнение регрессии описывает исследуемую зависимость. В общем случае .

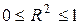Интервалы прогноза по линейному уравнению регрессии.

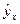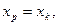В прогнозных расчетах по уравнению регрессии определяется предсказываемое у_р значение как точечный прогноз при т. е. путем подстановки в линейное уравнение регрессии 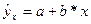соответствующего значения х. Однако точечный прогноз явно нереален, поэтому он дополняется расчетом стан­дартной ошибки 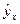, т. е. 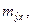и соответственно мы получаем ин­тервальную оценку прогнозного значения у*: .

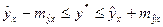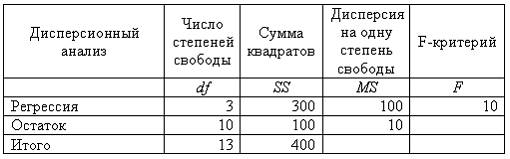
Таблица дисперсионного анализа.

Нелинейная регрессия

Соотношения между социально-экономическими явлениями и процессами далеко не всегда можно выразить линейными функциями, так как при этом могут возникать неоправданно большие ошибки. В таких случаях используют нелинейную регрессию. Таким образом, если между экономическими явлениями существуют нели­нейные соотношения, то они выражаются с помощью соответ­ствующих нелинейных функций: например, равносторонней ги­перболы 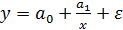, параболы второй степени 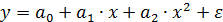и др.

Полулогарифмические модели.

Модели вида

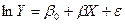
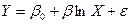
называются полулогарифмическими моделями.Такие модели обычно используют в тех случаях, когда необходимо определять темп роста или прироста каких-либо экономических показателей. Например, при анализе банковского вклада по первоначальному вкладу и процентной ставке, дефицит от темпа роста ВНП, темп роста инфляции от объема денежной массы и т. д .

Лог-линейная модель.

Логлинейный анализ является более «глубоким» методы исследования многомерных таблиц, а именно, этот метод посредством моделирования частот в таблице сопряженности позволяет проверить статистическую значимость различных факторов, присутствующие в таблице сопряженности и их взаимодействия. Логлинейный анализ имеет сходство с дисперсионным анализом и регрессионным анализом. Для проведения логлинейного анализа все переменные должны быть измерены в категориальной шкале.

14.Линейно-логарифмическая модель.

Y= β0 + βlnX+ ε (1)

Она сводится к линейной модели заменой X*= ln X. В данной модели коэффициент β определяет изменение переменной Y вследствие единичного относительного прироста X (например, на 1%), т.е. характеризует отношение абсолютного изменения Y к относительному изменению X. Действительно, продифференцировав

15.Обратная модель.

Модель вида

Y= β0 + β1·1/X+ ε называется обратной моделью. Эта модель сводится к линейной заменой Х*=1/Х. данная модель обычно применяется в тех случаях, когда неограниченное увеличение объясняющей переменной Х асимптотически приближает зависимую переменную Y к некоторому пределу

Степенная модель.

Степенная функция вида

Y=β0 + β1X + β2X2 + … + βmXm + ε (1)

часто отражает ту или иную экономическую зависимость. Например, кубическая функция

Y=β0 + β1X + β2X2 + β3X3 + ε (2)

в макроэкономике моделирует зависимость общих издержек (ТС) от объема выпуска (Q)

Y=β0 + β1X + β2X2 + ε (3)

может отражать зависимость между объемом выпуска (Q) и средними (АС) либо предельными (МС) издержками; или между расходами на рекламу (С) и прибылью (π) и т.д.

Показательная модель.

Показательная функция

Y=b0eβx (1)

Также достаточно широко применяется в эконометрическом анализе Наиболее важным ее приложением является ситуация, когда анализируется изменение переменной Y с постоянным темпом прироста во времени. В этом случае переменная Х символически заменяется переменной t:

Y=b0eβt (2)

8.Выбор формы модели.

Во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат и может использоваться для анализа и прогнозирования. Однако в силу однообразия и сложности экономических процессов ограничиться рассмотрением лишь линейных регрессионных моделей невозможно. Многие экономические зависимости не являются линейными по своей сути, и поэтому их моделирование линейными уравнениями регрессии, безусловно, не даст положительного результата. Например, при рассмотрении спроса Y на некоторый товар от цены X данного товара в ряде случаев можно ограничиться линейным уравнением регрессии: Y=β0+β1X . Здесь β1 характеризуетабсолютное изменение Y (в среднем) при единичном изменении X. Если же мы хотим проанализировать эластичность спроса по цене, то приведенное уравнение не позволит это осуществить. В этом случае целесообразно рассмотреть так называемую логарифмическую модель

При анализе издержек Y от объема выпуска X наиболее обоснованной является полиноминальная (точнее, кубическая) модель При рассмотрении производственных функций линейная модель является нереалистичной. В этом случае обычно используются степенные модели. Например, широкую известность имеет производственная функция Кобба-Дугласа Y=AKαLβ (здесь Y – объем выпуска; K и L – затраты капитала и труда соответственно; A, α и β – параметры модели).

19.Специфика множественная линейная регрессия (МЛР).

Однофакторные модели не всегда позволяют получить приемлемые результаты, поскольку любое экономическое явление подвержено влиянию значительного числа факторов. Поэтому возникает необходимость использования моделей множественной регрессии. Построение и анализ модели множественной регрессии имеет много общего с рассмотренным ранее эконометрическим моделированием парных зависимостей. Однако есть и специфические особенности. Они связаны с определением числа факторов, которые необходимо включить в модель.

Напомним, что модель множественной линейной регрессии имеет вид:

Y=b0+b1x1+b2x2+…bmxm, (15)

где m - количество независимых переменных.

Предпосылки МНК.

При оценке параметров уравнения регрессии применяется МНК. При этом делаются определенные предпосылки относительно составляющей, которая представляет собой ненаблюдаемую величину.

Исследования остатков - предполагают проверку наличия следующих пяти предпосылок МНК:1.случайный характер остатков; 2.нулевая средняя величина остатков, не зависящая от хi; 3.гомоскедастичность—дисперсия каждого отклонения,одинакова для всех значений х; 4.отсутствие автокорреляции остатков. Значения остатков, распределены независимо друг от друга; 5.остатки подчиняются нормальному распределению