Производная сложной функции

Пусть функция y=f(x) имеет производную в точке 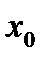,а функция z=F(y) имеет производную в точке 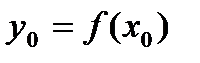, тогда сложная функция Ф(x)=F(f(x)) имеет производную в точке .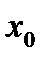

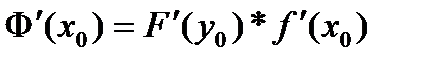Доказательство: Функция f(x) непрерывна в окрестности точки 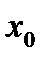, функция F(y) непрерывна в окрестности точки 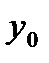, поэтому в окрестности точки 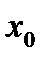существует сложная функция Ф(x).Функция F(y) имеет производную в точке 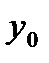, поэтому она дифференцируема в этой точке.

(\/)

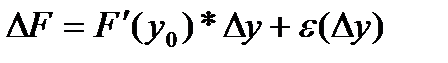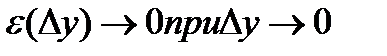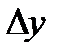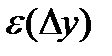-бесконечно малая более высокого порядка, чем , но может быть неопределенна в точке 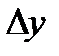=0, поэтому мы доопределяем ее по непрерывности в точке 0 : 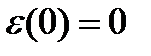.Разделим равенство (\/) на :

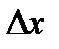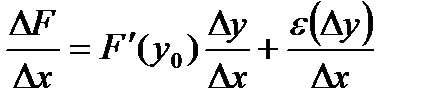
F(y)=F(y(x))=Ф(x) и тогда равенство запишем в виде 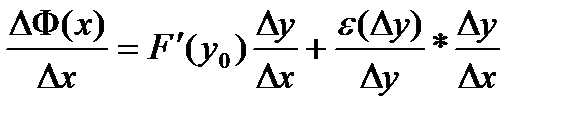. Перейдем к пределу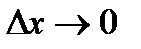

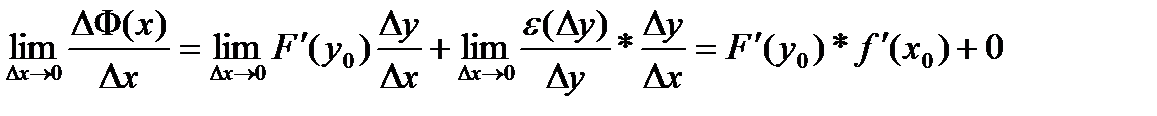. окажем, что 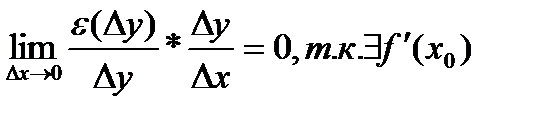, то y=f(x) непрерывна в окрестности точки 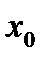, т.е. 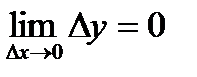( 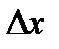и 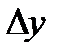стремятся к 0 одновременно), т.е. 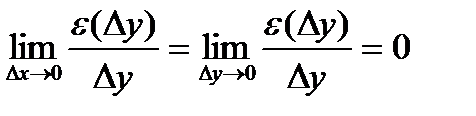(т.к. 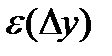бесконечно малая более высокого порядка, чем 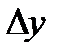), а 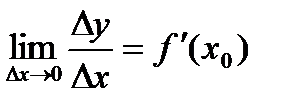, т.о. получим формулу .

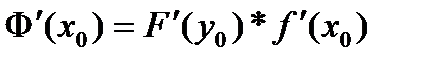БИЛЕТ 28. Дифференцирование обратной функции.

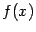
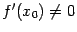
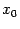
Теорема: Пусть функция имеет в точке производную . Тогда обратная

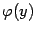
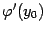
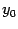
функция имеет в соответствующей точке производную , которую можно

отыскать по формуле.

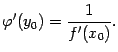(4.14)

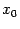
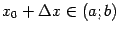
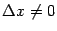
Доказательство: Дадим аргументу приращение , такое что , и

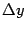
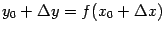рассмотрим соответствующее приращение , определяемое

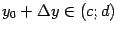
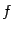
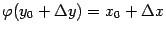равенством . Тогда, очевидно, ; при

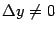
этом , а из монотонности функции следует, что . Поскольку

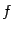
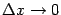
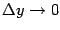
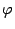
как функция , так и функция непрерывны, то условия и эквивалентны.

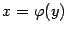
Составим теперь разностное отношение для функции и запишем для него очевидное равенство:

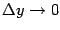
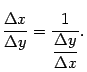
Теперь перейдём в этом равенстве к пределу при и учтём, что при этом 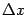тоже стремится к 0:

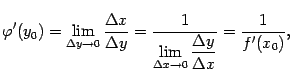
что мы и хотели доказать.

Заметим, что, очевидно, из формулы (4.14) следует, что

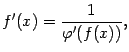(4.15)

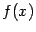
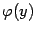если -- функция, обратная к .

БИЛЕТ 29. Производные высших порядков.

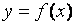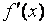Рассмотрим дифференцируемую функцию . Найдем её производную . Рассматривая как новую функцию, продифференцируем её:

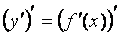
Полученную новую производную называют второй производной от функции 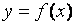. Вторую производную обозначают так:

или .

Аналогично находится производная третьего, четвертого, и т.д. n-го порядка. Третья производная обозначается так:

Четвертая:

.

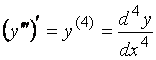Производной n – го порядка от функции 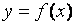называется производная от производной 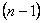-го порядка:

.

Производные высших порядков вычисляются последовательным дифференцированием данной функции.

БИЛЕТ 30. Теорема Ферма.

Теорема Ферма (необходимое условие extr):

Пусть 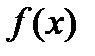определена на интервале (a,b) и точка 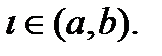если в точке 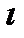функция f(x) достигает max или min значения и в точке 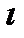существует производная, то f’( 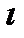)=0.

Доказательство.

Пусть для определенности в точке 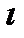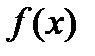принимает max значение, т.е 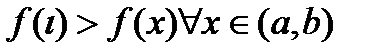. В точке 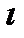существует производная 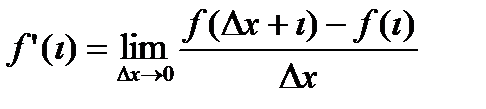, тогда 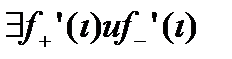(правая и левая производная).Распишем отношение

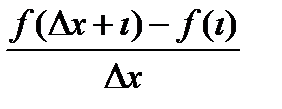
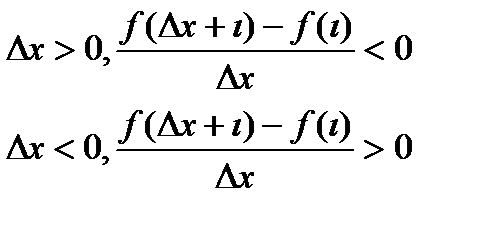переходя в этих интервалах к пределу, получим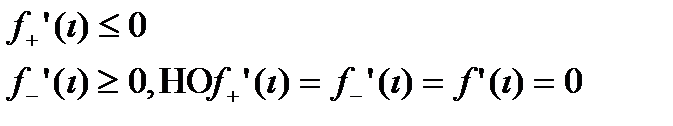

Замечание.

Теорема носит локальный характер, т.е. точка 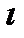является локальным экстремумом.