Доказательство: (метод деления пополам)

Теорема (о промежуточной последовательности).

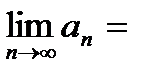
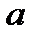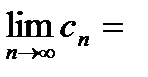
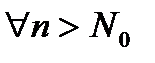
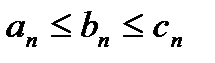Пусть , и . Тогда существует .

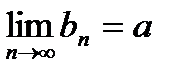Доказательство:

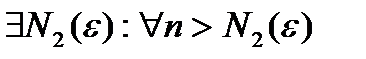
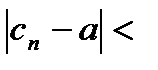
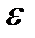
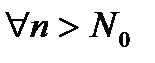
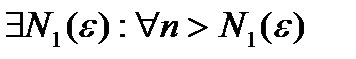
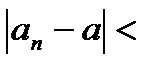
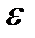
Возьмем произвольный .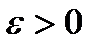

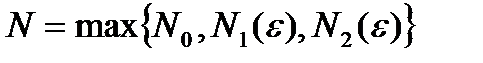. Тогда . . ( ).

.

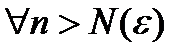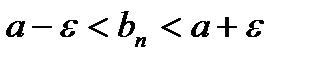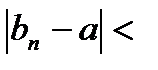
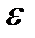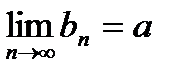Теорема: (об отделимости от нуля).

Пусть 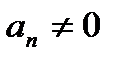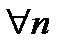и 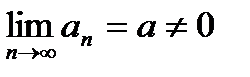. Тогда .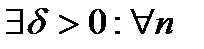

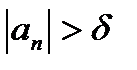Замечание: 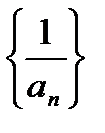- ограниченная.

( ).

. .

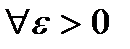
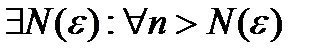
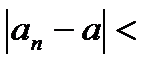
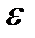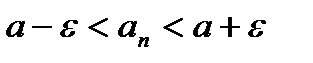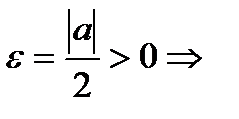
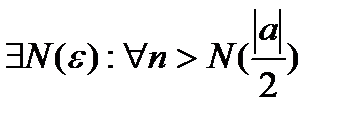
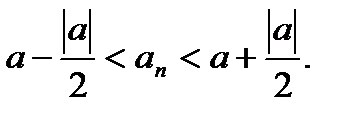
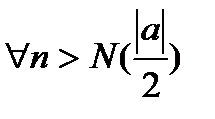
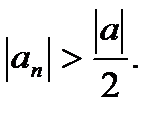
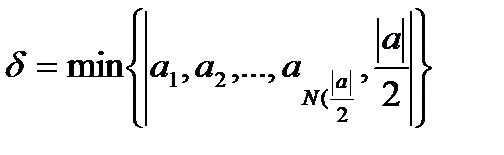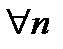
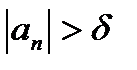БИЛЕТ 7. Монотонные последовательности. Теорема о пределе монотонной последо­вательности.

Определение: 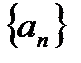-монотонно возрастающая (монотонно убывающая), если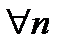 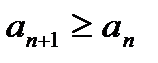( 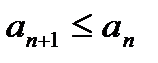). Если неравенства строгие, то последовательности строго возрастающие (убывающие).

Теорема (о пределе монотонной последо­вательности).Пусть 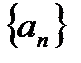-монотонно возрастает и ограничена сверху. Тогда она сходится, причем .

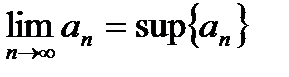Доказательство:

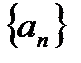ограничена сверху =>по теореме существования точной верхней грани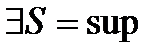 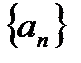. Докажем, что .

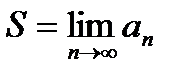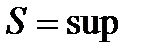
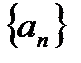: 1)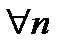

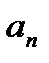
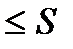
2) .

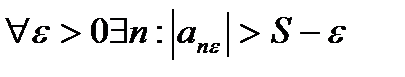Возьмем произвольный 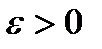, обозначим 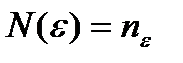из 2).

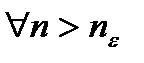1)=>

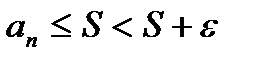
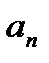
2)=> 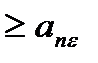(монот. возр).

Из этого следует, что , => .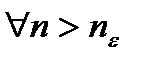

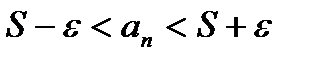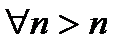
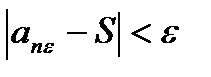Мы доказали достаточное условие числовой сходимости последовательности (монот. и огр.)

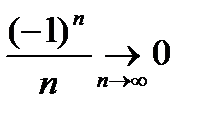(огр. на б.м.).

БИЛЕТ 8Подпоследовательности. Частичные пределы. Теорема о частичных пределах сходящейся подпоследовательности.

Определение: Пусть дана некая последовательность 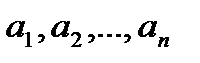. Из элементов этой последовательности извлечем другую последовательность 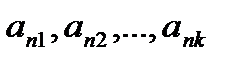, где последовательность 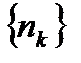-номера элементов исходной последовательности, причем 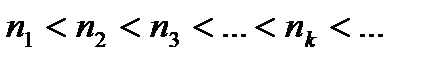Тогда последовательность 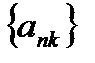-подпоследовательность последовательности .

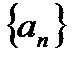Замечание: Элементы подпоследовательности выбираются в порядке их следования в исходной последовательности. .

Определение: Если 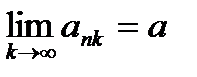, то -частичный предел последовательности .

Теорема (о частичных пределах сходящейся подпоследовательности): Пусть 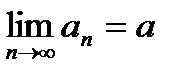, тогда .

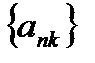
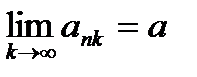Доказательство:

Возьмем произвольный 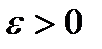, тогда .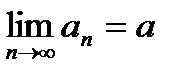

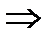
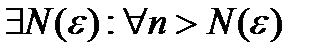
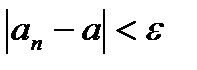Возьмем произвольную 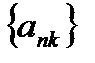. Обозначим 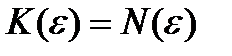. Тогда 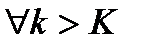имеем:

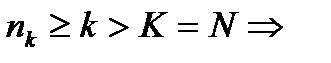
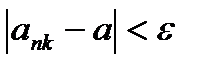. Таким образом:

.

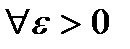
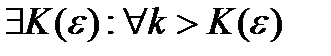
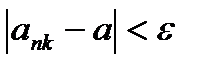Замечание: Понятие частичных пределов для сходящихся последовательностей не нужно.

БИЛЕТ 9. Лемма о вложенных отрезках.

Пусть 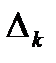= 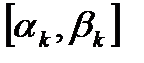, 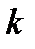=1,2,…, причем 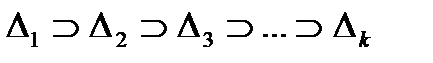…, то есть ,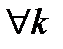

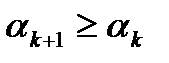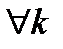
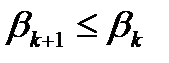. Тогда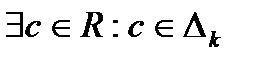 , то есть .

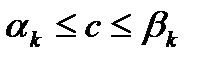Доказательство.

Рассмотрим 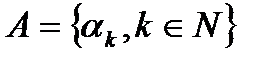, , 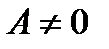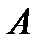ограничено сверху, так как любое 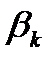является верхней границей множества 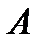в силу вложенности отрезков. 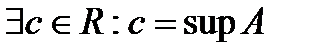.Тогда:

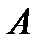а) - верхняя граница , то есть .

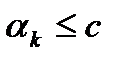б) - наименьшая из всех границ, то есть .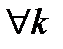

.

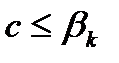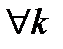
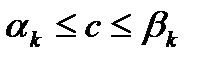Замечание:Если в условиях леммы хотя бы один из концов исключить, то аналогичная лемма будет не верна.

.

( ] ] ] ]

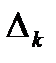
0 1/3 1/2 1

БИЛЕТ 10. Теорема Больцано-Вейерштрасса.

Теорема:Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Доказательство: (метод деления пополам).

I). Проведем построение системы отрезков.

ограниченная .

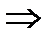
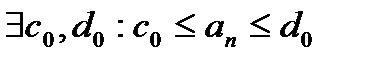
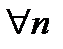
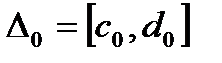Рассмотрим точку 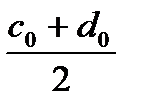- середину отрезка .

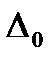1) В отрезке 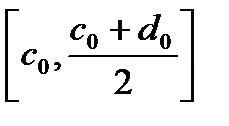содержится бесконечное число элементов .

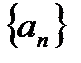Тогда , .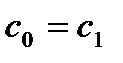

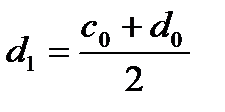2) В противном случае 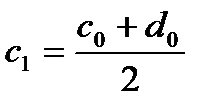, , 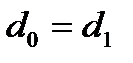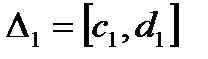-содержит бесконечное число элементов .

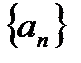Рассмотрим точку 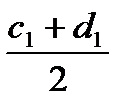- середину 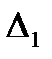и так далее.

1.

2. в содержится бесконечное число элементов .

3. .

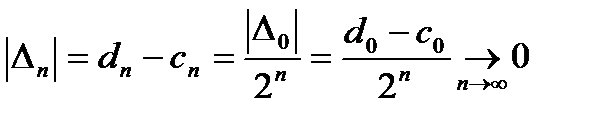II). Выбор подпоследовательности

По лемме о вложенных отрезках: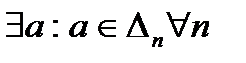

1) 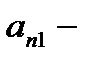произвольный элемент из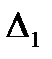

2) 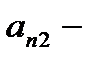элемент из :

………………………………………………….

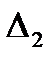k) 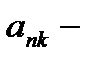элемент из :

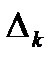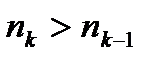
Докажем, что .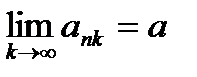

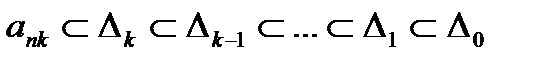
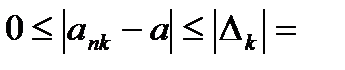
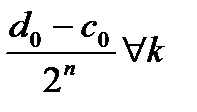
0 ( ).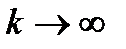

.

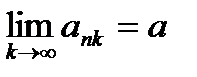БИЛЕТ 11. Критерий Коши сходимости последовательности.

Теорема (критерий Коши): Числовая последовательность сходится тогда и только тогда, когда она фундаментальна.

Замечание:Условие необходимости (=>), условие достаточности (<=), критерий- условие необходимости и достаточности (<=>).

1) Необходимость: (=>).

Пусть 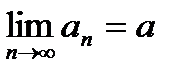. Возьмем произвольный 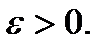Тогда .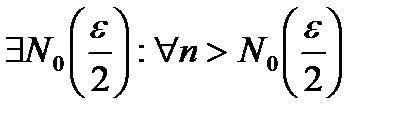

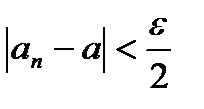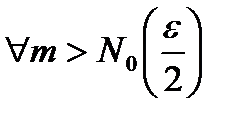
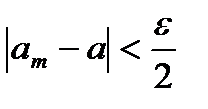. Обозначим 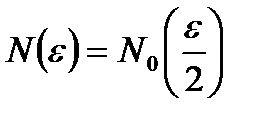, тогда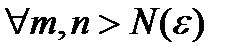

.

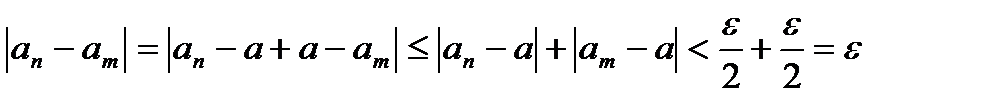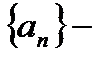фундаментальна.

2) Достаточность: (<=).

1. 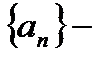фундаментальна => 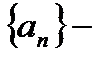ограниченная .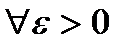

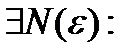
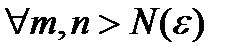
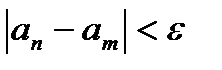Возьмем 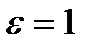, , 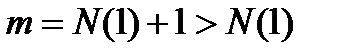тогда .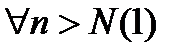

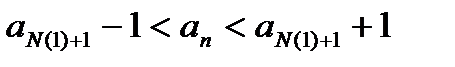Обозначим . .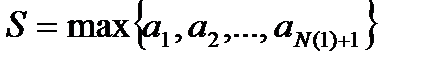

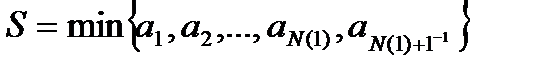ограничена.

2. Теорема Больцано-Вейерштрасса.

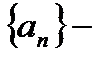ограниченная => 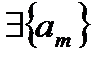- сходящаяся. Обозначим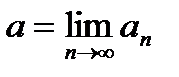

3. Докажем, что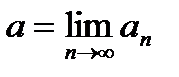

Возьмем произвольный 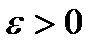. 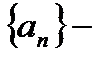фундаментальная => .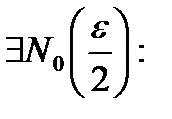

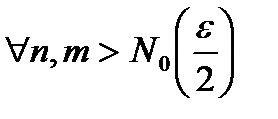
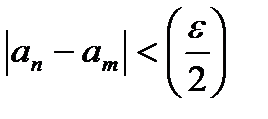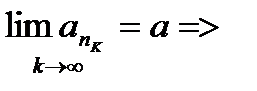
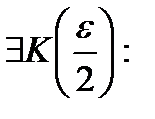
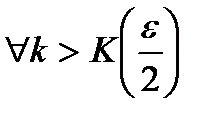
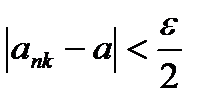
Обозначим 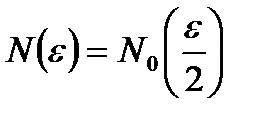и выберем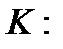

1) k>K

2)

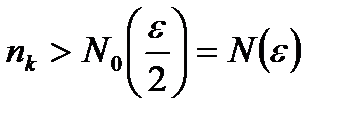
Тогда .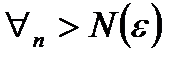

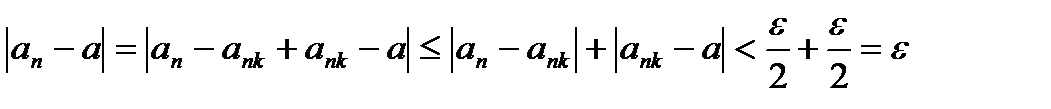. То есть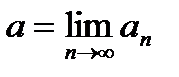

БИЛЕТ 12. Два определения предела функции. Эквивалентность определений.

Пусть 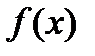определена в некоторой выколотой окрестности т.

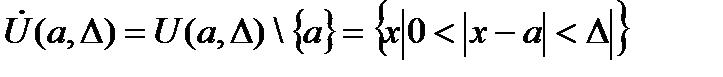
Определение 1 (Гейне): 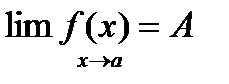, если , ,

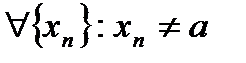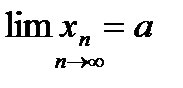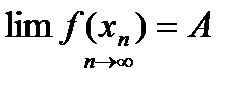
Замечание: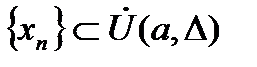

Определение 2 (Коши): 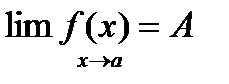, если .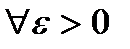

.

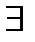
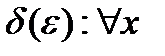
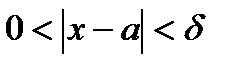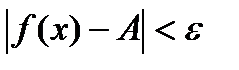Замечание: 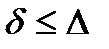, то есть .

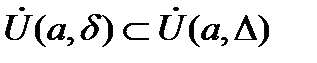Теорема:Определение 1 <=> Определение 2.

Имеем . .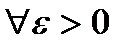

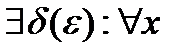
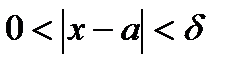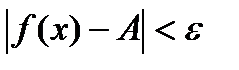Возьмем произвольную = => .

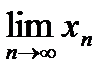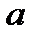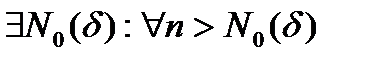
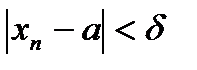Обозначим 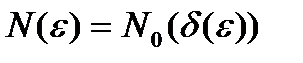. Тогда 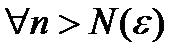0< .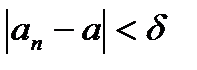

Т.обр.

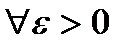
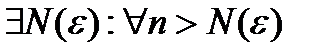
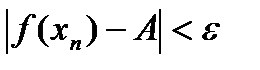., то есть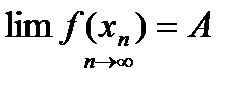

БИЛЕТ 13. Свойства пределов функций, связанные с неравенствами.

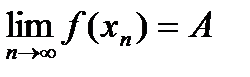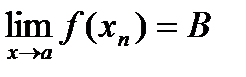Теорема:Пусть и , тогда .

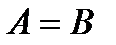Теорема: (Локальн. Огр.): Пусть 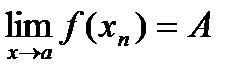, тогда , :

.

.

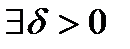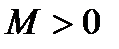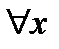
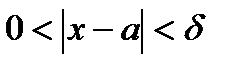
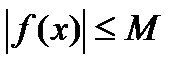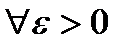
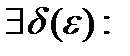
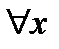
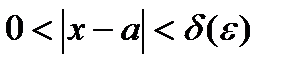
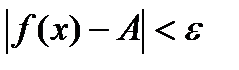Возьмем 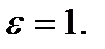Тогда .

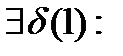
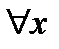
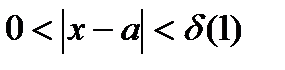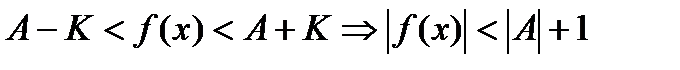
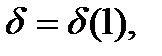
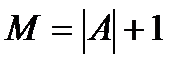
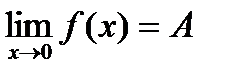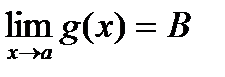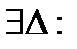
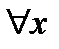
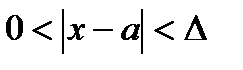
Теорема: Пусть , и 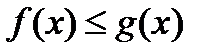. Тогда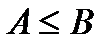

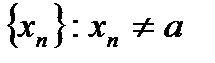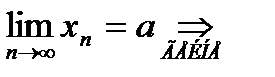
Возьмем произвольный , , 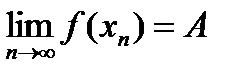, 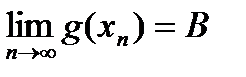причем .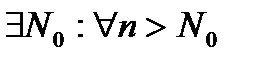

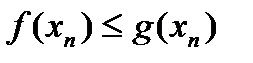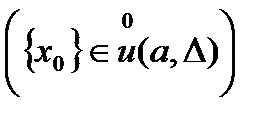
(по теореме о предельном переходе в неравенство) .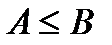

Теорема: Пусть 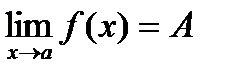, 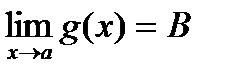и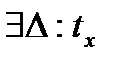

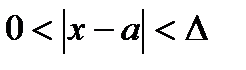
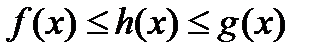. Тогда существует 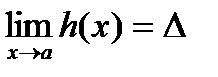. Возьмем произв. ,

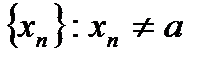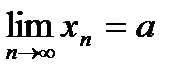
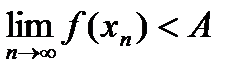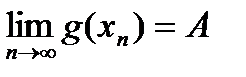, , причем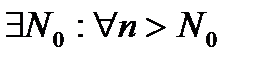

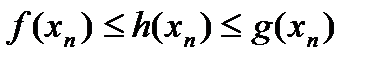
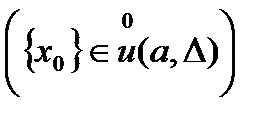
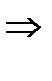сущ. .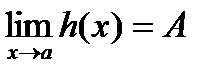

Теорема (об отделимости от нуля):Пусть , : .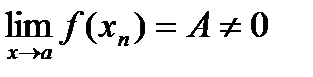

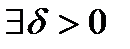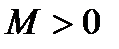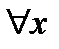
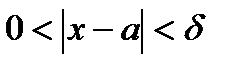
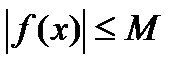Доказательство:

.

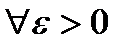
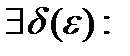
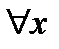
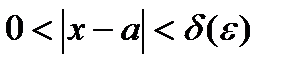
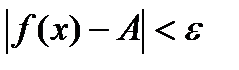Возьмем 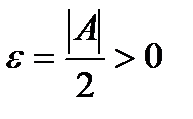, тогда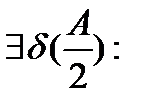

, , .

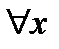
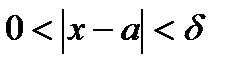
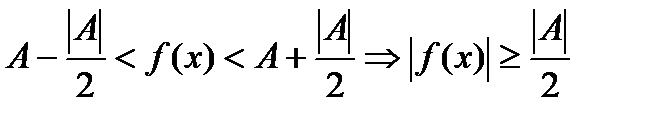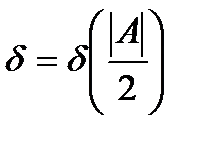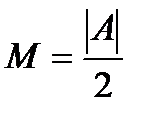БИЛЕТ 14. Свойства пределов функций, связанные с неравенствами. Теорема об арифметике пределов функций.

Теорема: (Локальн. Огр.): Пусть 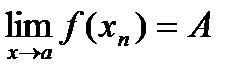, тогда , :

.

.

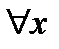
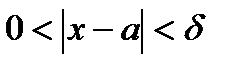
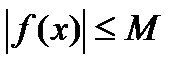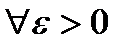
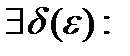
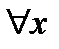
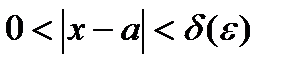
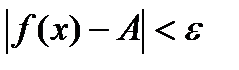Возьмем 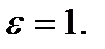Тогда .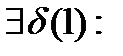

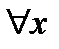
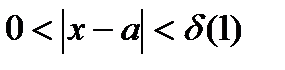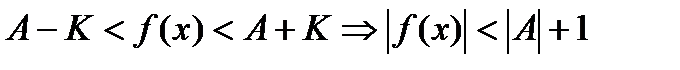
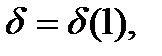
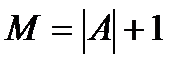
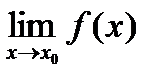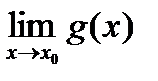Теорема: Если существуют и , то:

1). .

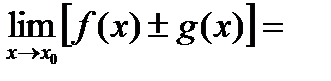
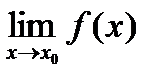
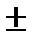
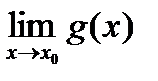2). 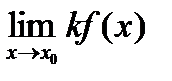= 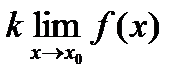( 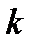- постоянная).

3). * .

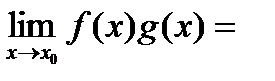
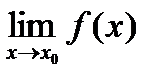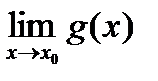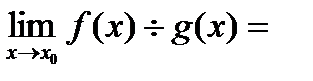
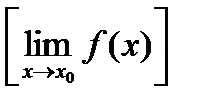
4). 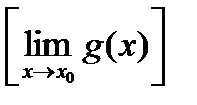, если .

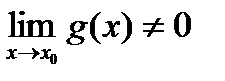Доказательства:

Доопределив по непрерывности функци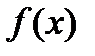и и 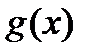в точке 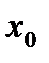, положив 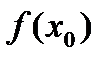= 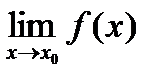и 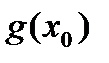= 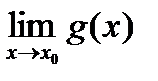(это изменение функций не влияет на их пределы). В точке 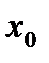будут непрерывны функции 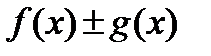, , 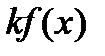, 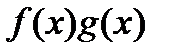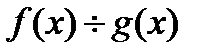(так как 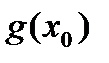= 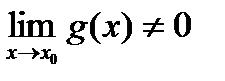. Поэтому в силу равенства 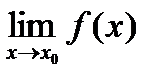= 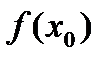получим:

1). = .

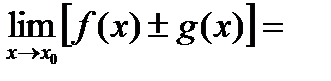
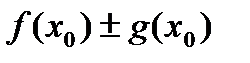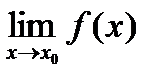
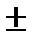
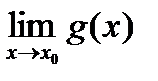2). = =

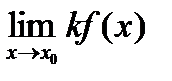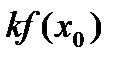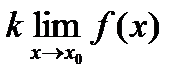
3). = * .

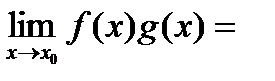
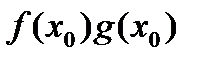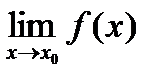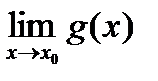4). = .

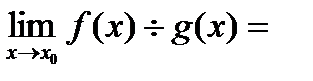
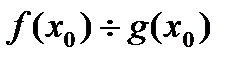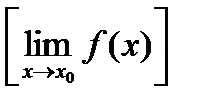
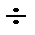
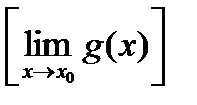БИЛЕТ 15. Разные виды пределов функции: бесконечно большие функции, пределы функции на бесконечности, односторонний предел. Теорема о связи односторонних пределов с пределом функции.

Определение 1: Функция 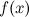называется бесконечно большой в точке , если для любого 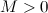существует такое 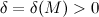, что для любого 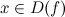, удовлетворяющего неравенству 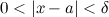, выполняется неравенство: 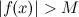. В этом случае пишут: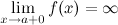

Определение 2: Число 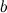называется пределом функции 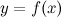на бесконечности или при 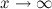, если для любого 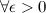существует число 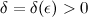такое, что для всех 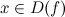из того, что 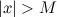, выполняется неравенство .

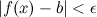Определение 3: Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.

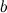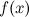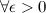
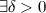Число называется правым пределом функции в точке , если для такое, что для любого 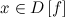и 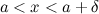, выполняется неравенство 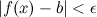(рис. 1). Правый предел обозначается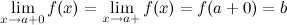

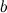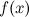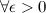
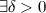Число называется левым пределом функции в точке , если для такое, что для любого 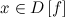и 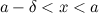, выполняется неравенство 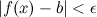(рис. 2). Левый предел обозначается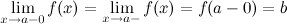

Теорема: Чтобы функция 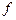имела предел в точке 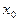, необходимо и достаточно чтобы она имела в этой точке оба односторонних предела и чтобы они были равны.

Функция 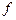называется непрерывной в точке 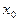, если .

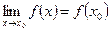Если в этом определении раскрыть определение предела на языке « 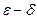», то получим определение: функция 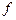называется непрерывной в точке 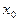, если .

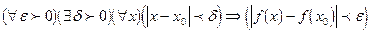Если же раскрыть определение предела на языке последовательностей, то приходим к определению: функция 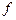называется непрерывной в точке 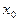, если для любой последовательности 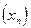, сходящейся к 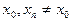, соответственная последовательность значений функции 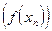сходится к .

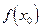Иногда удобно формулировать определение непрерывности функции на языке приращений. Разность 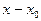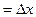называют приращением аргумента в точке 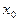, а разность 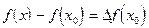называют приращением функции 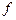в точке .

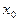Функция 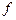называется непрерывной в точке 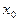, если приращение функции в точке 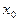стремится к нулю при стремлении к нулю приращения аргумента, т.е. .

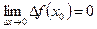БИЛЕТ 16. Первый замечательный предел (с доказательством). Второй замечательный предел (без доказательства).

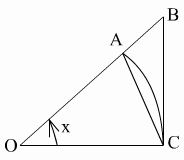
Первый замечательный предел:

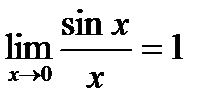
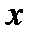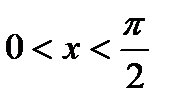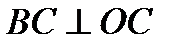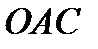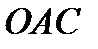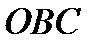Для доказательства возьмем вектор окружности радиуса 1 с центральным углом, равным (радиан), и проведем . Тогда пл. < пл. сект. < пл. или 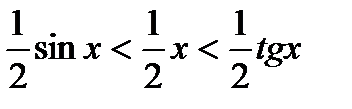. Разделив все части этого неравенства на 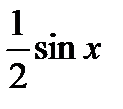> 0, получим

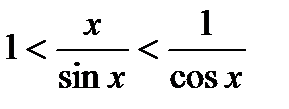или 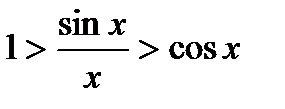. Это неравенство, доказанное для любых 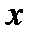из интервала (0; 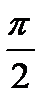), верно для любого 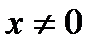из интервала (- 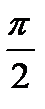; 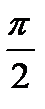) в силу четности функций, входящих в это неравенство.

Докажем, что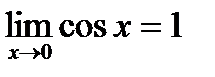

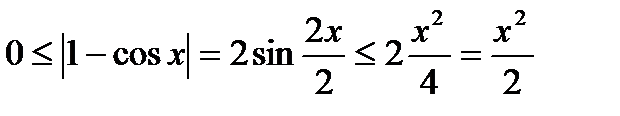( ) при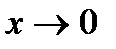

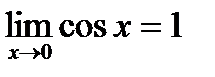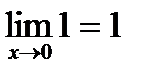А раз и , то .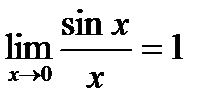

Кроме того: 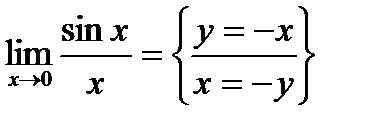= 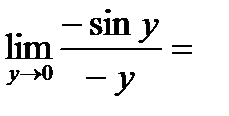1

Второй замечательный предел:

.

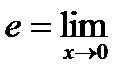
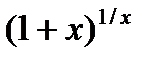На первый взгляд кажется, что 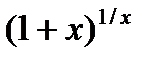при 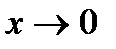имеет пределом единицу (так как 1+ 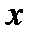при 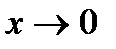имеет пределом единицу, а единица в любой степени есть единица). Но в степень 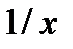возводится 1+ 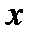, а не единица. И вот из-за этой бесконечно малой добавки 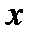предел не равен единице. Чтобы приблизительно представить себе поведение функции 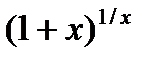при малых 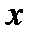приведем таблицу значений этой функции:

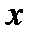	1/2	1/3	1/4	0.01	0.001
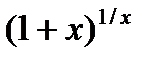	2.25	2.37…	2.44…	2.7047…	2.7169…

Из этой таблицы видно, что с уменьшением 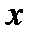функция увеличивается. Оказывается, что это имеет место для всех 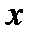>0, а из этого следует, что функция имеет предел.