Теорема 6.1 (Кронекера–Капелли)
Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу её расширенной матрицы:
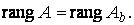
Для совместной системы линейных уравнений вопрос о её определённости или неопределённости решается с применением следующих теорем.
Теорема 6.2. Если ранг основной матрицы совместной системы равен числу неизвестных, то система является определённой
Теорема 6.3. Если ранг основной матрицы совместной системы меньше числа неизвестных, то система является неопределённой.
Таким образом, из сформулированных теорем вытекает способ исследования систем линейных алгебраических уравнений. Пусть n – количество неизвестных, 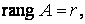
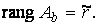 Тогда:
Тогда:
1)при 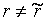 система несовместна;
система несовместна;
2)при  система совместна, причём, если
система совместна, причём, если 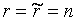 , система
, система
определённая; если же 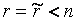 , система неопределённая.
, система неопределённая.
Определение 6.1. Базисным решением неопределённой системы линейных уравнений называют такое её решение, в котором все свободные неизвестные равны нулю.
Пример. Исследовать систему линейных уравнений. В случае неопределённости системы найти её базисное решение.

Вычислим ранги основной 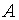 и расширенной матриц
и расширенной матриц 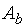 данной системы уравнений, для чего приведём расширенную (а вместе с тем и основную) матрицу системы к ступенчатому виду:
данной системы уравнений, для чего приведём расширенную (а вместе с тем и основную) матрицу системы к ступенчатому виду:
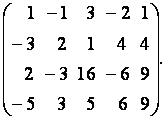
Вторую строку матрицы сложим с её первой строкой, умноженной на 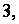 третью строку – с первой строкой, умноженной на
третью строку – с первой строкой, умноженной на 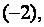 а четвёртую строку – с первой, умноженной на
а четвёртую строку – с первой, умноженной на 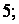 получим матрицу
получим матрицу
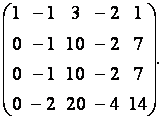
К третьей строке этой матрицы прибавим вторую строку, умноженную на 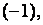 а к четвёртой строке – первую, умноженную на
а к четвёртой строке – первую, умноженную на 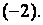 В результате получим матрицу
В результате получим матрицу
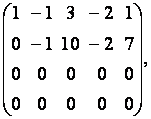
удаляя из которой третью и четвёртую строки получим ступенчатую матрицу
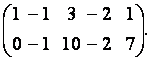
Таким образом, 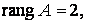
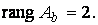 Следовательно, данная система линейных уравнений совместна, а поскольку величина ранга меньше числа неизвестных, система является неопределённой. Полученной в результате элементарных преобразований ступенчатой матрице соответствует система уравнений
Следовательно, данная система линейных уравнений совместна, а поскольку величина ранга меньше числа неизвестных, система является неопределённой. Полученной в результате элементарных преобразований ступенчатой матрице соответствует система уравнений
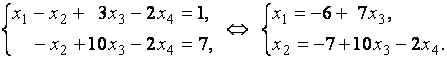
Неизвестные 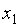 и
и 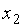 являются главными, а неизвестные
являются главными, а неизвестные 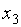 и
и 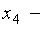 свободными. Придавая свободным неизвестным нулевые значения, получим базисное решение данной системы линейных уравнений:
свободными. Придавая свободным неизвестным нулевые значения, получим базисное решение данной системы линейных уравнений:
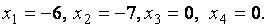
Задания для самостоятельной работы по теме
«Системы линейных уравнений и методы их решения»
Вариант 1
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
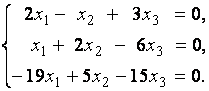
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
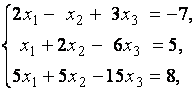
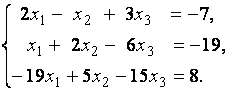
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти их базисные решения.
Вариант 2
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
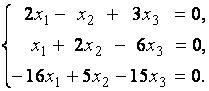
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
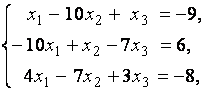
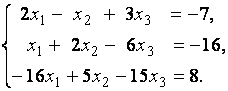
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 3
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
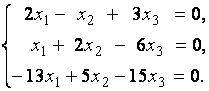
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
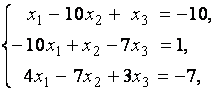
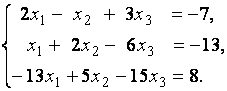
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 4
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
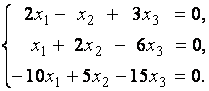
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
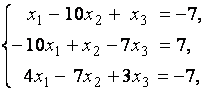
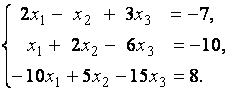
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 5
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
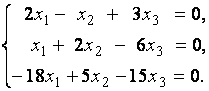
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
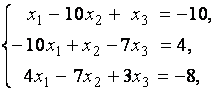
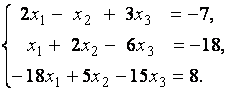
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 6
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
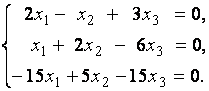
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
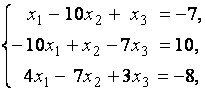
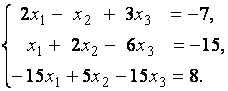
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 7
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
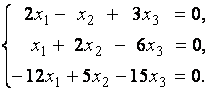
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
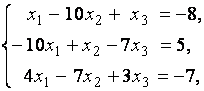
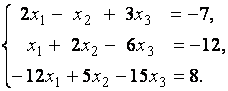
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 8
1. Решить систему линейных уравнений
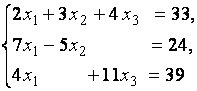
методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
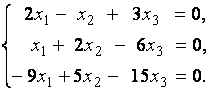
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
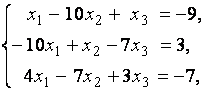
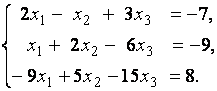
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 9
1. Решить систему линейных уравнений
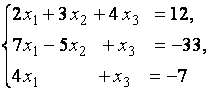
методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
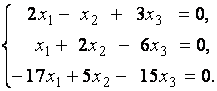
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
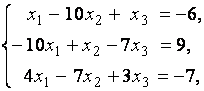
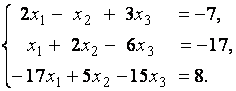
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 10
1. Решить систему линейных уравнений
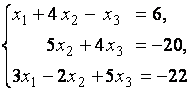
методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
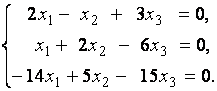
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
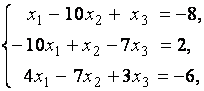
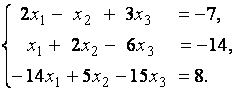
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 11
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
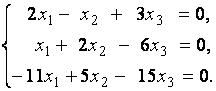
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
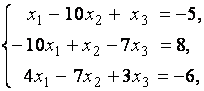
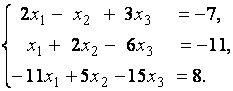
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 12
1. Решить систему линейных уравнений
методом Гаусса, матричным методом и методом Крамера.
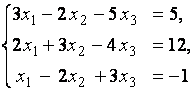
2. Дана однородная система линейных уравнений
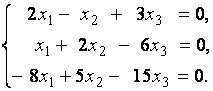
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
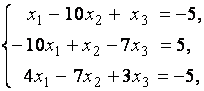
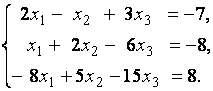
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 13
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
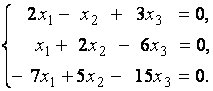
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
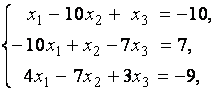
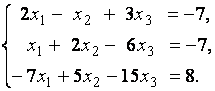
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 14
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
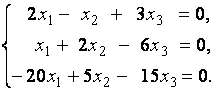
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
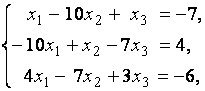
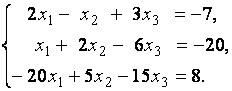
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 15
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
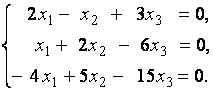
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
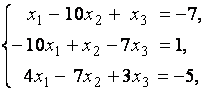
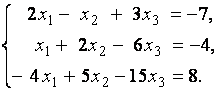
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 16
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
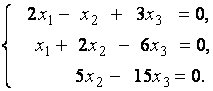
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
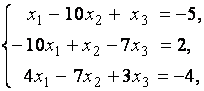
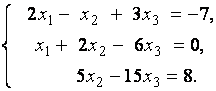
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 17
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
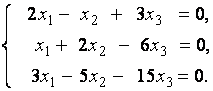
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
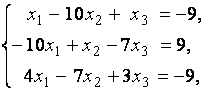
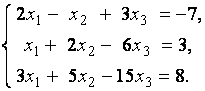
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 18
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
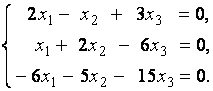
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
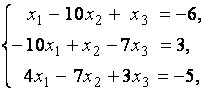
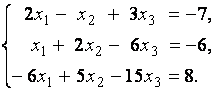
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 19
1. Решить систему линейных уравнений
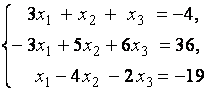
методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
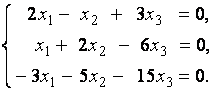
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
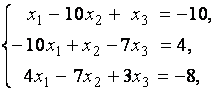
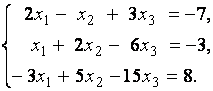
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 20
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
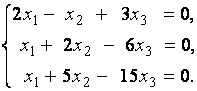
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
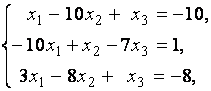
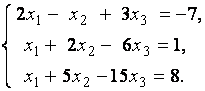
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 21
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
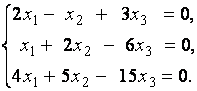
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
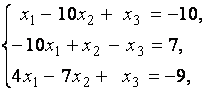
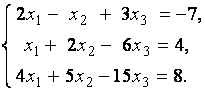
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 22
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
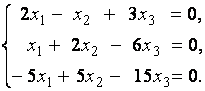
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
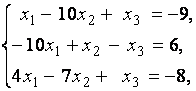
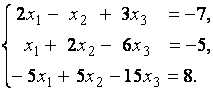
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 23
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
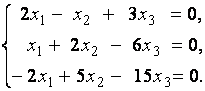
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
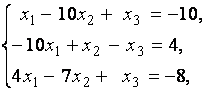
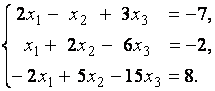
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 24
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
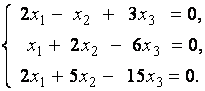
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
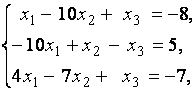
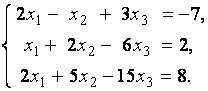
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 25
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
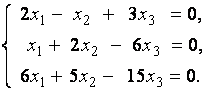
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
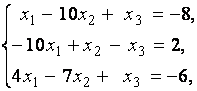
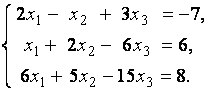
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 26
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
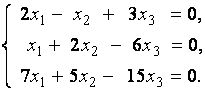
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
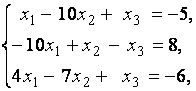
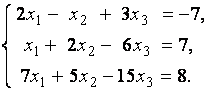
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 27
1. Решить систему линейных уравнений
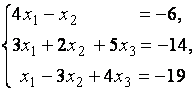
методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
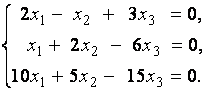
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
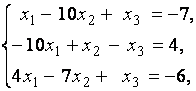
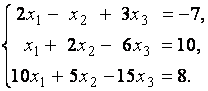
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 28
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
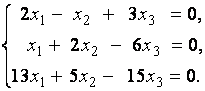
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
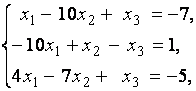
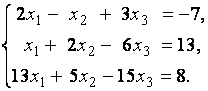
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 29
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
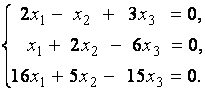
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
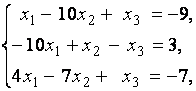
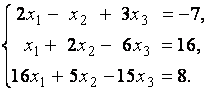
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
Вариант 30
1. Решить систему линейных уравнений

методом Гаусса, матричным методом и методом Крамера.
2. Дана однородная система линейных уравнений
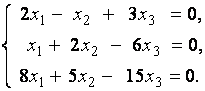
Выяснить, имеет ли эта система уравнений нетривиальное решение. В случае утвердительного ответа найти это решение.
3. Даны системы линейных уравнений
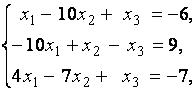
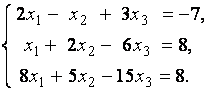
Исследовать системы линейных уравнений и классифицировать их. В случае неопределённости системы уравнений найти общее и базисное решения.
