Тригонометрические подстановки

Литература: [3], гл. X, §§ 11, 14

[5], Ч.2, гл. 9, § 9.5

Рассмотрим некоторые типы интегралов, содержащие иррациональные выражения.

1) , где R – рациональная функция своих аргументов.

Пусть k – наименьший общий знаменатель дробей (другими словами k – наименьшее общее кратное натуральных чисел n, q, …, s). Сделаем подстановку: , . Тогда каждая дробная степень x выражается через целую степень t и, следовательно, подынтегральная функция преобразуется в рациональную функцию относительно t (многочлен или рациональную дробь), методы интегрирования которой рассмотрены выше.

Пример 1.

2) , где R – рациональная функция своих аргументов, .

Пусть , где k – как и прежде, наименьший общий знаменатель дробей . Тогда . С помощью такой подстановки подынтегральная функция преобразуется в рациональную функцию относительно t.

Пример 2.

3) , где R – рациональная функция своих аргументов, .

Подынтегральную функцию можно рационализировать с помощью подстановки , откуда , .

Рассмотрим теперь интегралы вида , , , где R – функция, рациональная относительно своих аргументов. Если интегралы не являются табличными, то избавиться в подынтегральной функции от квадратного корня можно с помощью, так называемых, тригонометрических подстановок.

4) .

Пусть , тогда , .

Пример 3.

Теперь в ответе надо перейти к х. Это удобнее всего сделать с помощью прямоугольного треугольника. Из подстановки находим . Вспоминаем, что в прямоугольном треугольнике равен отношению противолежащего катета х к гипотенузе 2. По теореме Пифагора находим третью сторону треугольника, а затем по этому треугольнику можно находить любую тригонометрическую функцию угла t.

х

t

Из рисунка видно , .

Итак, .

5) .

Пусть , тогда , , .

Пример 4.

х

t

, .

6) .

Пусть , тогда , .

Пример 4.

х

t

, ,

.

.

Интегрирование в элементарных функциях

Литература: [3], гл. X, § 16

Как было сказано в п. 2.1, всякая функция f (x), непрерывная на [a, b], имеет на этом промежутке первообразную. Однако не всякая первообразная является элементарной функцией.

Например, функция 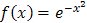непрерывна на всей числовой прямой, следовательно, её первообразная, а, значит, и , существует на любом промежутке. Но в элементарных функциях первообразная этой функции не выражается.

О функциях, первообразные которых существуют, но не являются элементарными функциями, говорят, что они не интегрируемы в элементарных функциях. А интегралы от таких функций называются неберущимися в элементарных функциях.

К таким интегралам относятся, например: , , , , и т.д.

ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ