Проверка теоретических знаний. Занятие 3. Однородные уравнения

Занятие 3. Однородные уравнения

Цель занятия - развитие у обучающихся личностных качеств, а также направлено на овладение следующими общекультурными компетенциями:

· навыками межличностных отношений; готовностью к работе в команде;

· знаниями этических норм и использованием их в профессиональной деятельности;

· принятием различий и мультикультурности;

· способностью применять знания на практике;

· способностью приобретать новые знания, используя современные образовательные и информационные технологии;

· фундаментальной подготовкой по основам профессиональных знаний и готовностью к использованию их в профессиональной деятельности;

· навыками работы с компьютером;

· способностью к анализу и синтезу;

профессиональными компетенциями:

1) в сференаучно-исследовательской деятельности:

· умением понять поставленную задачу;

· пониманием корректности постановок задач;

· глубоким пониманием сути точности фундаментального знания;

· способностью передавать результат проведенных физико-математических и прикладных исследований в виде конкретных рекомендаций, выраженных в терминах предметной области изучавшегося явления;

· умением публично представить собственные и известные научные результаты;

· владением проблемно-задачной формой представления математических знаний;

2) в сфере проектной и производственно-технологической деятельности:

· способностью осуществлять целенаправленный поиск информации о новейших научных и технологических достижениях в сети Интернет и из других источников;

· знанием и следование в жизни кодексу профессиональной этики;

· способностью формировать суждения о значении и последствиях своей профессиональной деятельности с учетом социальных, профессиональных и этических позиций;

· пониманием сущности и значения информации в развитии современного общества; владение основными методами, способами и средствами получения и переработки информации.

Проверка теоретических знаний

1. Какая функция f(x,y) называется однородной степени п.

(Если справедливо равенство 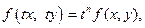то функция называется однородной,где n – порядок однородности.)

2. Какое дифференциальное уравнение 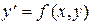называется однородным.

(Если его правая часть - однородная функция нулевого порядка.)

3. Как однородное уравнение можно преобразовать в уравнение с разделяющимися переменными.

(Сохраняя прежнюю независимую переменную х, введем новую искомую функцию u = y/х, откуда .)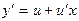

4. В какое уравнение преобразуется исходное после предложенной замены.

(Исходное уравнение преобразуется в уравнение, допускающее разделение переменных .)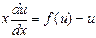

5. Какое преобразование переменных сохраняет вид однородного уравнения.

(Если рассмотреть преобразование подобия плоскости с центром подобия в точке (0,0): х₁ = kx, у₁ = ky. Это преобразование не изменит вид уравнения, а, следовательно, не меняет всей совокупности решений уравнения. Таким образом, все интегральные кривые однородного уравнения могут быть получены из одной кривой при помощи преобразования гомотетии с центром гомотетии в начале координат.)

6. Какой вид функции f(x,y) в дифференциальных уравнениях 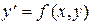допускает сведение к однородному.

(Функция вида 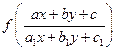допускает сведение к однородному уравнению.)

7. Какую подстановку необходимо выполнить, чтобы привести уравнение к однородному виду.

(Введение вместо х и у новых переменных x и h: 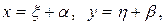где a и b - постоянные, приводит исходное уравнение к однородному)

8. Как определяются постоянные .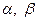

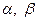( определяются так, чтобы числитель и знаменатель преобразованного уравнения не содержал свободных членов.)

9. Всегда ли можно найти a и b.

(a и b определяются из линейной системы

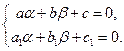
Это возможно, если .)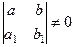

10. Если a и b найдены, то к какому виду преобразуется исходное уравнение.

(В этом случае уравнение преобразуется к однородному

)

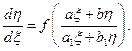11. Что делать, если условие 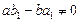не выполняется.

(В этом случае имеет место пропорциональность 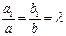, , 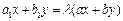поэтому надо ввести вместо у новую функцию и: )

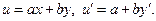12. Какое уравнение получается после введения предложенной подстановки.

(Получим уравнение с разделяющимися переменными

)

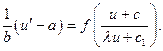13. Существуют ли еще какие – либо подходы приведения неоднородных уравнений к однородному виду.

(Некоторые уравнения можно привести к однородным заменой 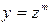(число m заранее неизвестно).)

14. Как определяется число т.

(Чтобы его найти, надо в уравнении сделать замену переменной 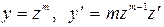, и потребовать, чтобы все члены уравнения стали однородными.)

15. В каком случае определение т возможно.

(Это не всегда возможно, т.к. на одно число m составляется несколько уравнений, система переопределена, и ее решение не всегда существует.)

16. Какой вывод можно сделать, если определение т невозможно.

(Если же такого m найти нельзя, то уравнение не приводится к однородному.)

Практические задания

Пример 1. Найти кривые, у которых подкасательная равна сумме абсциссы и ординаты точки касания.

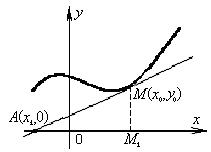Рис. 1

Решение: По условию отрезок проекции касательной АМ (где М имеет координаты 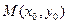) на ось ОХ равен АМ₁ (рис. 1). Тогда

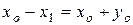. (1)

Точка А (х₁, 0) удовлетворяет уравнению касательной к кривой 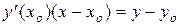, тогда 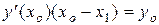. С учетом формулы (1) и произвольности точки М, получаем дифференциальное уравнение

.

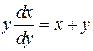Полученное уравнение является однородным. Введя новую переменную 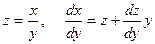, получаем уравнение с разделяющимися переменными 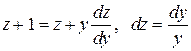. Интегрируя обе части равенства, получим ln Су = z. Возвращаясь к прежней переменной, получим решение

.

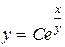Пример 2. Решить уравнение

.

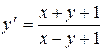Решение: Так как определитель правой части отличен от нуля, то чтобы свести уравнение к однородному, перенесем начало координат в точку с координатами (a, b), то есть заменим 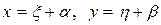. Подставляя в исходное уравнение, получим

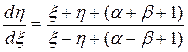. (2)

Подбираем числа a и b так, чтобы

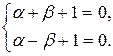
Это возможно, т.к. определитель системы отличен от нуля a = -1, b = 0.

Пусть 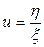и 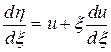, тогда (2) примет вид

.

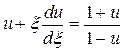Разделяя переменные 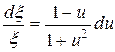и интегрируя, получим

.

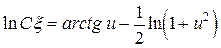С учетом вновь введенных переменных

,

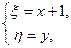
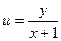общее решение уравнения перепишем так:

.

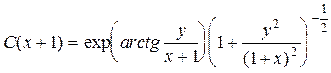Пример 3. Привести уравнение 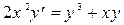к однородному.

Решение: После замены 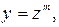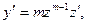получаем равенство вида:

.

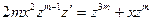Чтобы все члены имели один и тот же вес необходимо выполнение равенства степеней всех членов, 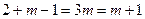, это возможно при 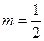, следовательно замена имеет вид: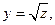 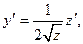и уравнение переходит к однородному виду 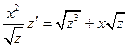или 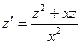.