Предельная полезность и MRS
Функция полезности (и предельная полезность, как выяснится далее) могут быть использованы для измерения предельной нормы замещения.
Представим изменение в потреблении каждого блага (Dx1, Dx2), которое сохраняет неизменной полезность. Тогда мы должны иметь
MU1Dx1 + MU2Dx2 = DU = 0.
Алгебраический знак MRS получается отрицательным. Однако, принято не обращать внимания на знак и брать MRS в абсолютном выражении (или по модулю).
Значение предельной полезности зависит от выбора функции полезности. Но соотношение предельных полезностей не зависит от монотонной трансформации функции полезности, т.е. от способа представления предпочтений.
Лекция 2.3. ОПТИМАЛЬНЫЙ ВЫБОР ПОТРЕБИТЕЛЯ.
Оптимальный выбор.
Ранее мы говорили: экономическая модель потребительского выбора такова, что люди выбирают наилучший набор благ, какой они могут себе позволить. Теперь можно выразиться более профессионально: потребители выбирают наиболее предпочтительный набор из их бюджетного множества.
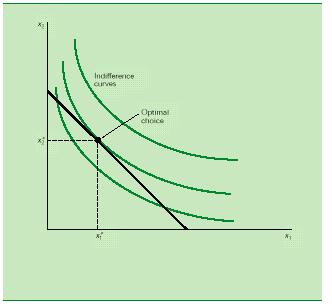
Это типичный случай.
Здесь мы хотим набор из бюджетного множества, который находится на наиболее высоко расположенной кривой безразличия. Так как здесь типичные предпочтения (больше - лучше), мы рассмотрим только те наборы, которые находятся на бюджетной линии. Если двигаться из правого угла вдоль бюджетной линии, то мы передвигаемся на все более высокие кривые безразличия. Итак до тех пор, пока кривая безразличия не коснется бюджетной линии ® (х1*,х2*).
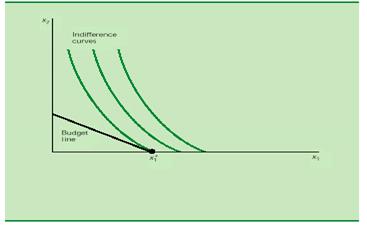 Интересный случай. Точка оптимума, когда потребление одного из благ равно нулю.
Интересный случай. Точка оптимума, когда потребление одного из благ равно нулю.
Наклон кривой безразличия и наклон бюджетной линии не совпадают. Но: кривая безразличия не пересекает бюджетную линию. Наблюдается угловой оптимум в отличие от внутреннего оптимума.
Далее, ограничим анализ только типичными ситуациями, где существует внутренний оптимум. Итак, необходимое условие оптимума - кривая безразличия касается линии бюджета. Но является ли это достаточным условием?
Условие касания - необходимое условие оптимума, но не достаточное. Если кривые безразличия – строго выпуклые, тогда будет только один оптимальный набор на каждой кривой безразличия. Условие, что MRS равна наклону кривой безразличия - очевидно на графике (при внутреннем оптимуме). Но что это означает экономически?
Что если MRS ¹ P1/P2
MRS= DX2/D X1=-1/2; P1/P2=1
Это означает, что потребитель готов отказаться от двух единиц блага 1, чтобы получить 1 единицу блага 2. Но рынок готов обменять 1: 1. Тогда индивид, конечно, будет отказываться от блага 1, чтобы получить больше блага 2. В любом случае, когда MRS¹ P1/P2-нет оптимума.
