Осцилляторда өрнектелу (ОӨ) әдісімен азөлшемді кванттық жүйелер спектрлерін есептеу
(1.1) Шредингер теңдеуін ОӨ әдісімен шешуге кірісейік [16]. Бұл әдіс өрістің скалярлық кванттық теориясының идеяларына және әдістеріне негізделген. Әдістің толық сипаттамасы [12] жұмыста баяндалған. Әдістің артықшылығы, оның аясында алынған потенциалдардың кең класы үшін ауытқу теориялар қатары өте тез үйлеседі. Нөлдік жуықтаудағы байланысқан жүйе гамильтонианының негізгі күйі кейбір Ω эффективті жиілігі бар осцилляторлық толқындық функциямен бейнеленеді деп болжанады. Ω жиілігі байланысқан күй беретін потенциалдан негізгі кванттық үлесін ескеретіндей анықталады. Ол үшін бастапқы гамильтониандағы әзірге белгісіз Ω жиілігі бар осцилляторлық бөлігі бөлініп алынады, ал каноникалық айнымалыларды, координата және импульсті 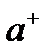 туу және
туу және 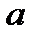 жою операторлары арқылы өрнектеледі, содан кейін оларды қалыпты түрде реттейді. Ары қарай осылай түрленген гамильтонианда каноникалық айнымалылар бойынша сызықты және квадраттық қосылғыштар болмауы қажет. Бұл шарт Ω - осциллятор жиілігін анықтайды және осцилляторда өрнектелу шарты деп аталады. Осылайша, алынған ауытқу теорияларының қатары эффективті қосылады.
жою операторлары арқылы өрнектеледі, содан кейін оларды қалыпты түрде реттейді. Ары қарай осылай түрленген гамильтонианда каноникалық айнымалылар бойынша сызықты және квадраттық қосылғыштар болмауы қажет. Бұл шарт Ω - осциллятор жиілігін анықтайды және осцилляторда өрнектелу шарты деп аталады. Осылайша, алынған ауытқу теорияларының қатары эффективті қосылады.
R1 бірөлшемді кеңістіктегі жүйе гамильтонианы:
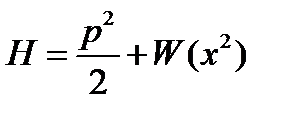 (1.4.1)
(1.4.1)
мұндағы:
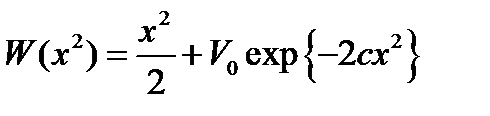 (1.4.2)
(1.4.2)
потенциалдық энергия. Таза осцилляторлық бөлігін жазамыз:
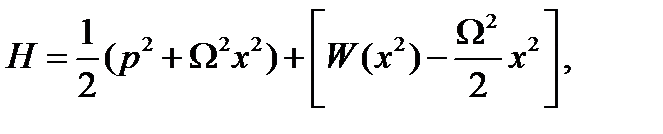 (1.4.3)
(1.4.3)
мұндағы Ω әзірге ерікті оң параметр болып табылады. 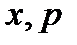 каноникалық айнымалыларын туу және жою операторлары арқылы көрсетейік:
каноникалық айнымалыларын туу және жою операторлары арқылы көрсетейік:
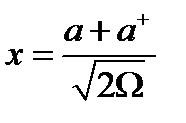
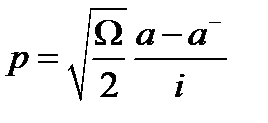 (1.4.4)
(1.4.4)
Ары қарай 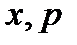 каноникалық айнымалыларға арналған өрнектерді (1.4.3)-ге қоямыз және туу және жою операторлары бойынша реттейміз. Сонда қалыпты түрде көрсетілген потенциал мына түрге ие болады ([12]-ден толығырақ қараңыз):
каноникалық айнымалыларға арналған өрнектерді (1.4.3)-ге қоямыз және туу және жою операторлары бойынша реттейміз. Сонда қалыпты түрде көрсетілген потенциал мына түрге ие болады ([12]-ден толығырақ қараңыз):
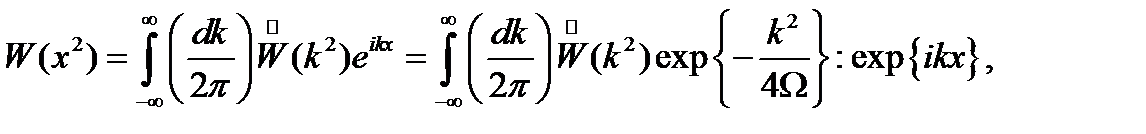 (1.4.5)
(1.4.5)
мұндағы ~ - нормалдану символы және
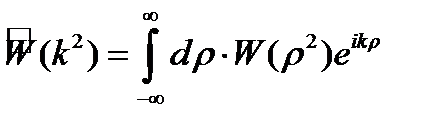 (1.4.6)
(1.4.6)
Осы қатынастарды қолдана отырып, (3.3) гамильтонианды қайта жазайық ([12]-ден толығырақ қараңыз):
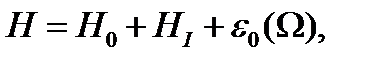 (1.4.7)
(1.4.7)
мұндағы
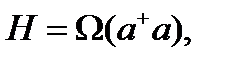
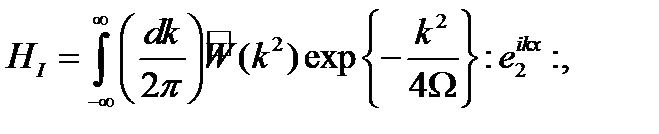
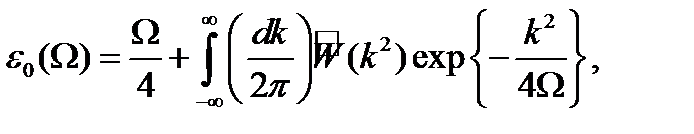
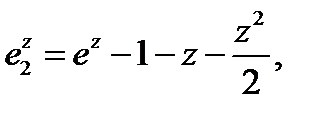
ал 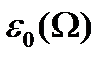 - негізгі күй немесе (1.4.3) гамильтониан вакуумының энергиясы. Осцилляторда өрнектелу әдісінің шартынан алынған
- негізгі күй немесе (1.4.3) гамильтониан вакуумының энергиясы. Осцилляторда өрнектелу әдісінің шартынан алынған  үшін теңдеу
үшін теңдеу  бойынша
бойынша 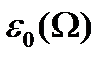 минимум энергияны анықтайтын теңдеумен сәйкес келеді:
минимум энергияны анықтайтын теңдеумен сәйкес келеді:
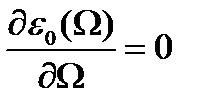 (1.4.8)
(1.4.8)
 осциллятор жиілігі
осциллятор жиілігі 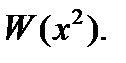 потенциалының бастапқы параметрлерінің функциясы болып табылады.
потенциалының бастапқы параметрлерінің функциясы болып табылады.
Осылайша, 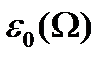 негізгі күй энергиясын есептеу үшін,
негізгі күй энергиясын есептеу үшін,  жиілігі үшін (1.4.8) теңдігі орындалу қажет.
жиілігі үшін (1.4.8) теңдігі орындалу қажет. 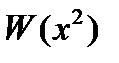 потенциалдың нақты түрін қолдана отырып, келесі оңтайландырылған есепке келеміз:
потенциалдың нақты түрін қолдана отырып, келесі оңтайландырылған есепке келеміз:
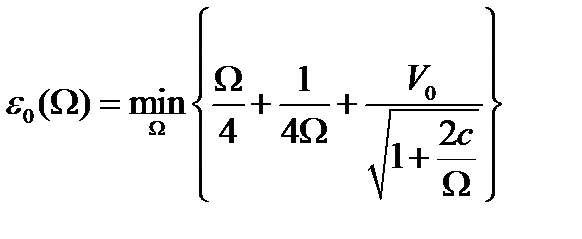
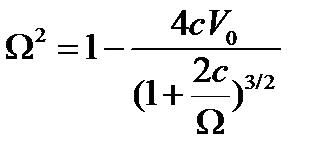 (1.4.9)
(1.4.9)
(1.4.9)-дегі  үшін теңдеу жалғыз бір оң айғақты түбірге ие болады.
үшін теңдеу жалғыз бір оң айғақты түбірге ие болады.
Гамильтонианның бастапқы есебіндегі 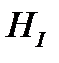 әсерлесуінің белгіленуі ауытқу теориясының (АТ) аясында деңгей энергиясына жоғарғы түзетулерді есептеуге мүмкіндік береді. ОК-тегі АТ бірінші реті нөлге тең. Екінші реті мына формуламен анықталады ([12]-ден толығырақ қараңыз)
әсерлесуінің белгіленуі ауытқу теориясының (АТ) аясында деңгей энергиясына жоғарғы түзетулерді есептеуге мүмкіндік береді. ОК-тегі АТ бірінші реті нөлге тең. Екінші реті мына формуламен анықталады ([12]-ден толығырақ қараңыз)
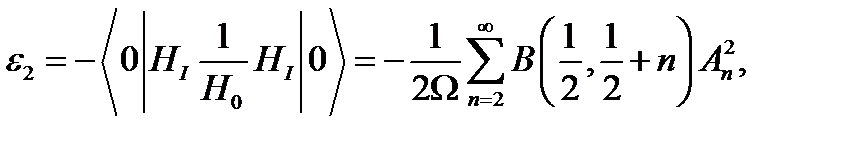 (1.4.10)
(1.4.10)
мұндағы
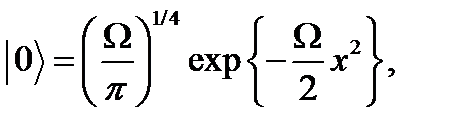 (1.4.11)
(1.4.11)
ОӨ әдісіндегі негізгі күйдің толқындық функциясы, ал 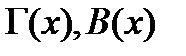 - сәйкес гамма және бета функциялар,
- сәйкес гамма және бета функциялар,
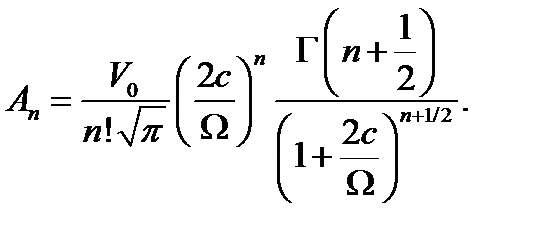 (1.4.12)
(1.4.12)
Осылайша, (1.4.1) бастапқы гамильтонианның негізгі күйінің энергиясы
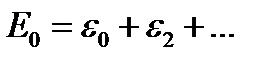 (1.4.13)
(1.4.13)
Әртүрлі әсерлесу потенциалының параметрлері кезіндегі ОӨ әдісімен есептеу нәтижелері 4-7 суреттерде көрсетілген. Графиктерде сондай-ақ ОӨ әдісінің ауытқу теориясының екінші ретіне сәйкес келетін қисықтар көрсетілген.
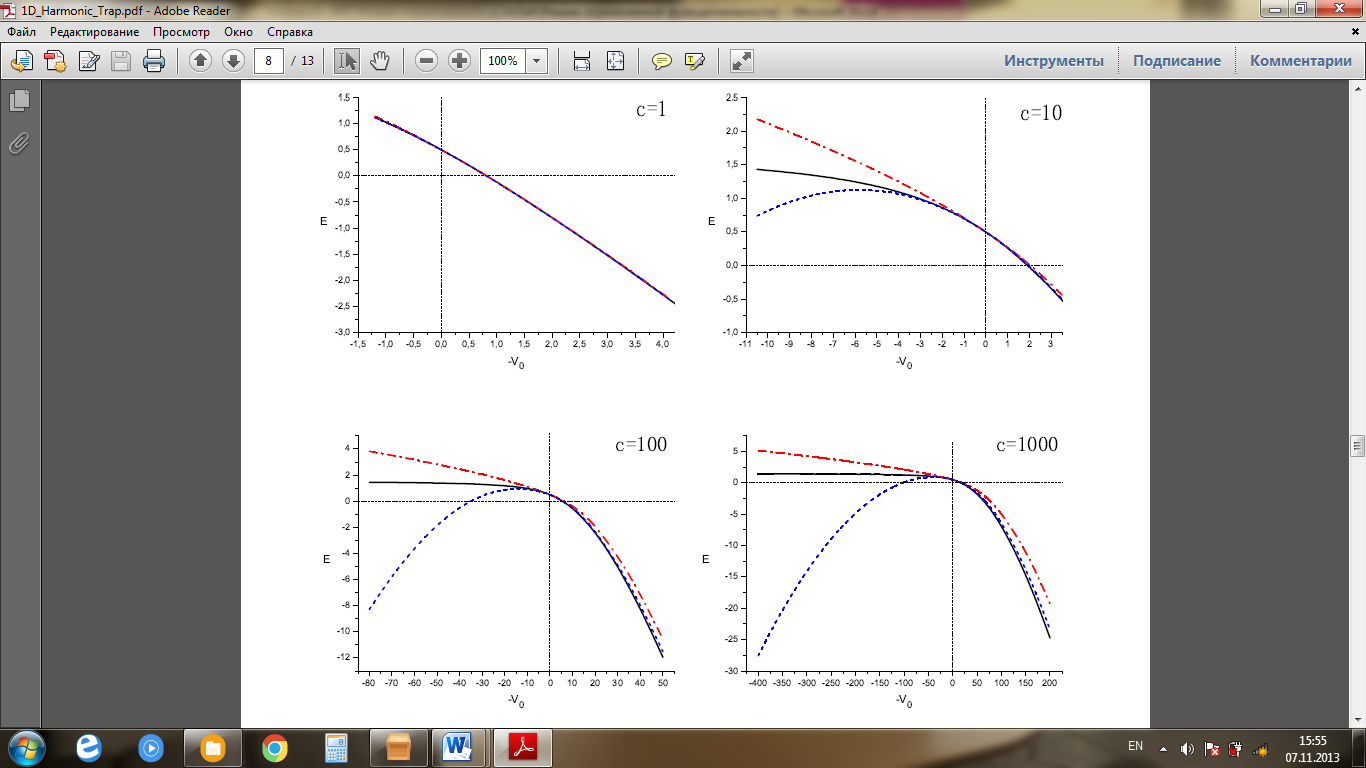
Тұтас сызықтар – энергияның сандық есептелуі. Штрих үзік сызықтар – ОӨ әдісінің нөлдік жуықтауындағы энергия. Үздік сызықтар – ОӨ әдісіндегі екінші жуықтаудағы энергия.
Сурет 4 – (1.1) теңдеуі үшін ОӨ әдісінің қолданылу аймағы
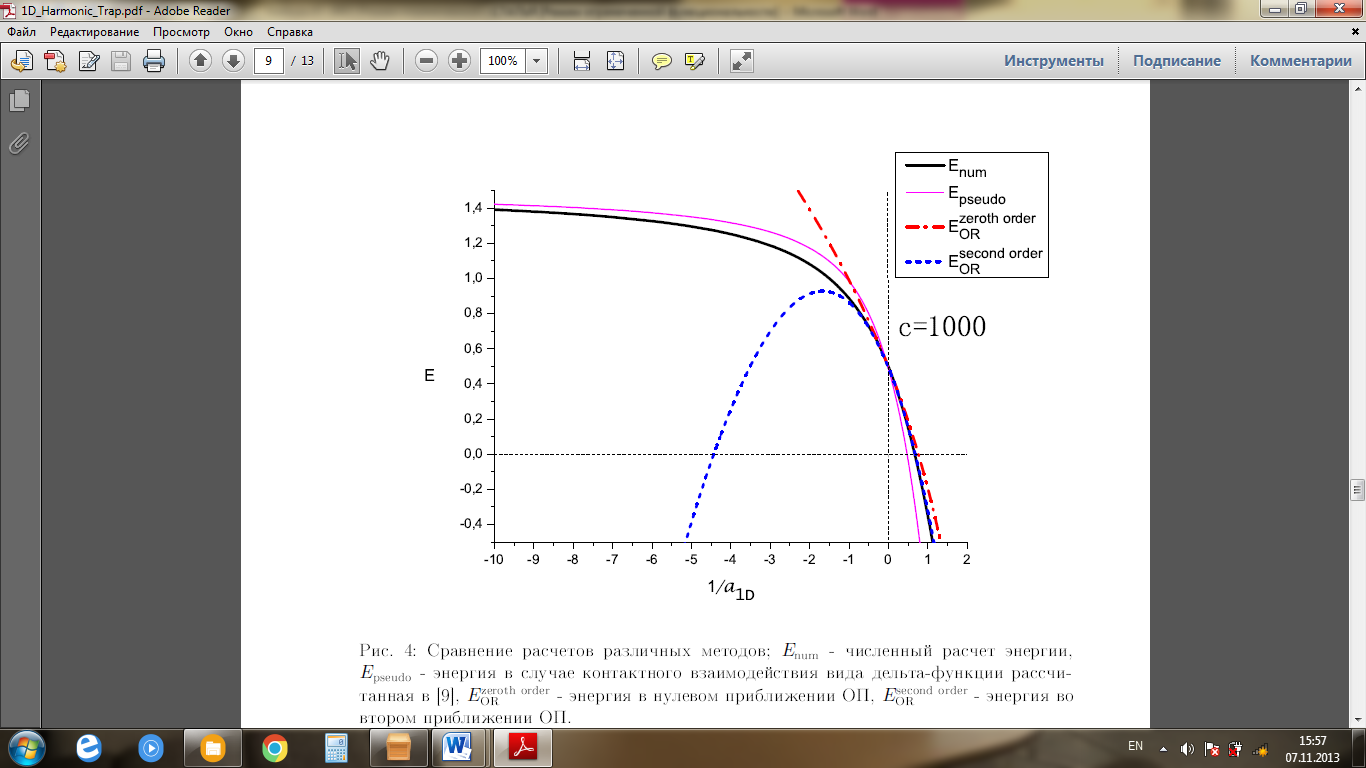
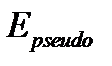 - [25]-да есептелген дельта-функция түріндегі қосылған әсерлесу жағдайындағы энергия,
- [25]-да есептелген дельта-функция түріндегі қосылған әсерлесу жағдайындағы энергия, 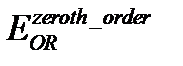 - ОӨ нөлдік жуықтаудағы энергия,
- ОӨ нөлдік жуықтаудағы энергия, 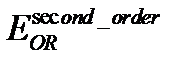 - ОӨ екінші жуықтаудағы энергия.
- ОӨ екінші жуықтаудағы энергия.
Сурет 5 – Әртүрлі әдістердің есептерін салыстыру; 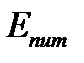 - энергияның сандық есептелуі
- энергияның сандық есептелуі
4-суретте әрқайсысында үш қисығы бар графиктер көрсетілген. Екі қисық ОӨ әдісімен есептеуге сәйкес келеді, ал үшіншісі сандық әдіспен есептелген. Бірінші графикте үш қисық қосылады да екі әдістің жақсы сәйкес келуі бақыланады. Графиктерден көрініп тұрғандай, 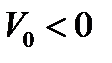 теріс мәндер кезінде ОӨ әдісі
теріс мәндер кезінде ОӨ әдісі 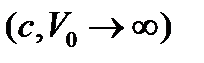 кезіндегі сандық мәндерден ауытқи бастайды. ОӨ әдісіндегі екінші ретті АТ дәл осы потенциал параметрлері кезінде аз ауытқиды және
кезіндегі сандық мәндерден ауытқи бастайды. ОӨ әдісіндегі екінші ретті АТ дәл осы потенциал параметрлері кезінде аз ауытқиды және 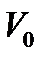 теріс аймақтарында өте жақсы дәлдік көрсетеді. Алайда, оң
теріс аймақтарында өте жақсы дәлдік көрсетеді. Алайда, оң 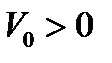 үшін нөлдік сияқты, ОӨ әдісіндегі екінші ретті АТ да
үшін нөлдік сияқты, ОӨ әдісіндегі екінші ретті АТ да 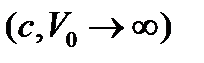 кезінде сандық есептеуден айтарлықтай ауытқиды.
кезінде сандық есептеуден айтарлықтай ауытқиды.
5-суретте ОӨ әдісімен есептеулер сандық есептеулермен және кері шашырау ұзындығына тәуелді дельта-функция түріндегі псевдопотенциалды қолдану арқылы [8]-де жүргізілген есептеулермен салыстырылады.
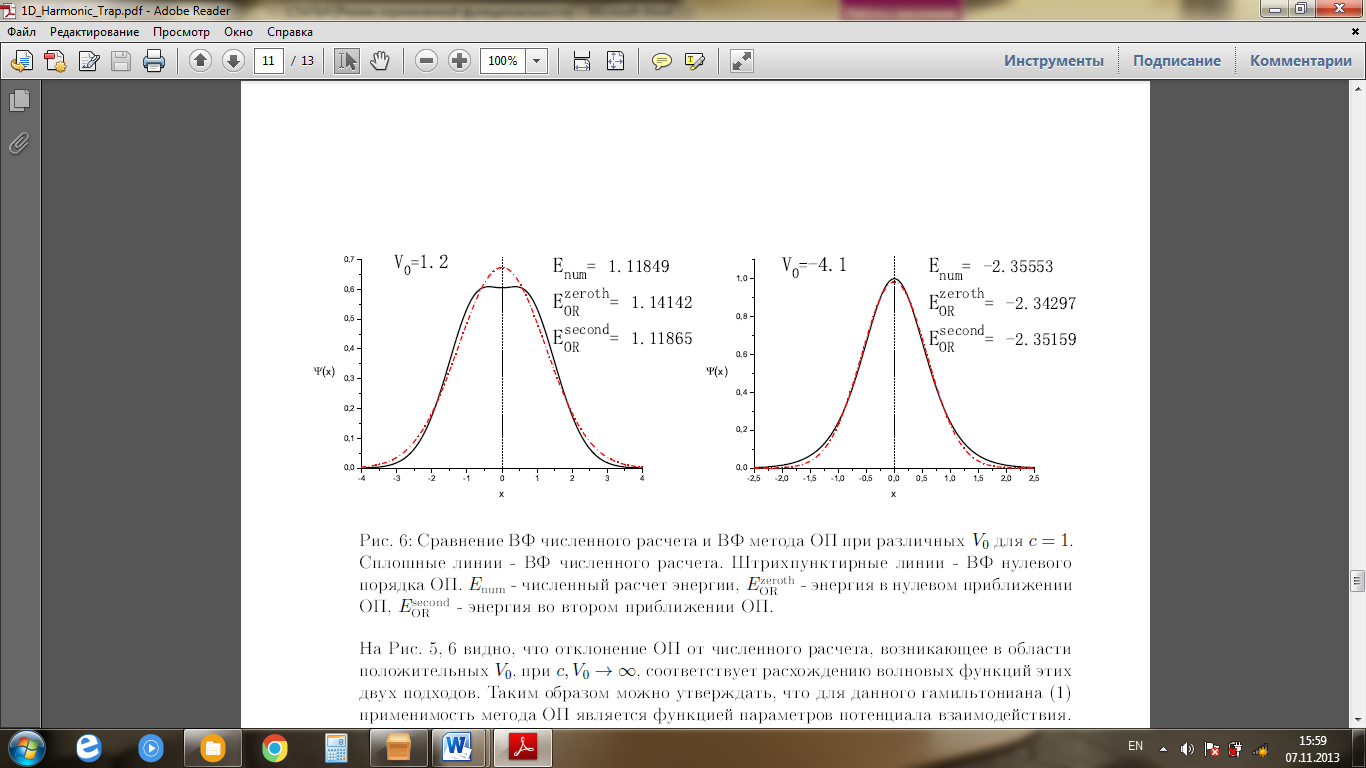
Әртүрлі потенциал параметрлері кезінде ОӨ әдісінің ауытқу себебі ОӨ-те толқындық функция, нөлдік жуықтауда (1.4.11) гауссианмен бейнеленеді. Осылайша ОӨ әдісінің ауытқуы осцилляторлық толқындық функцияның гаусстық түрінің шынайы ТФ түрінен ауытқуымен түсіндіріледі, оны 6- және 7-суреттерден көруге болады.
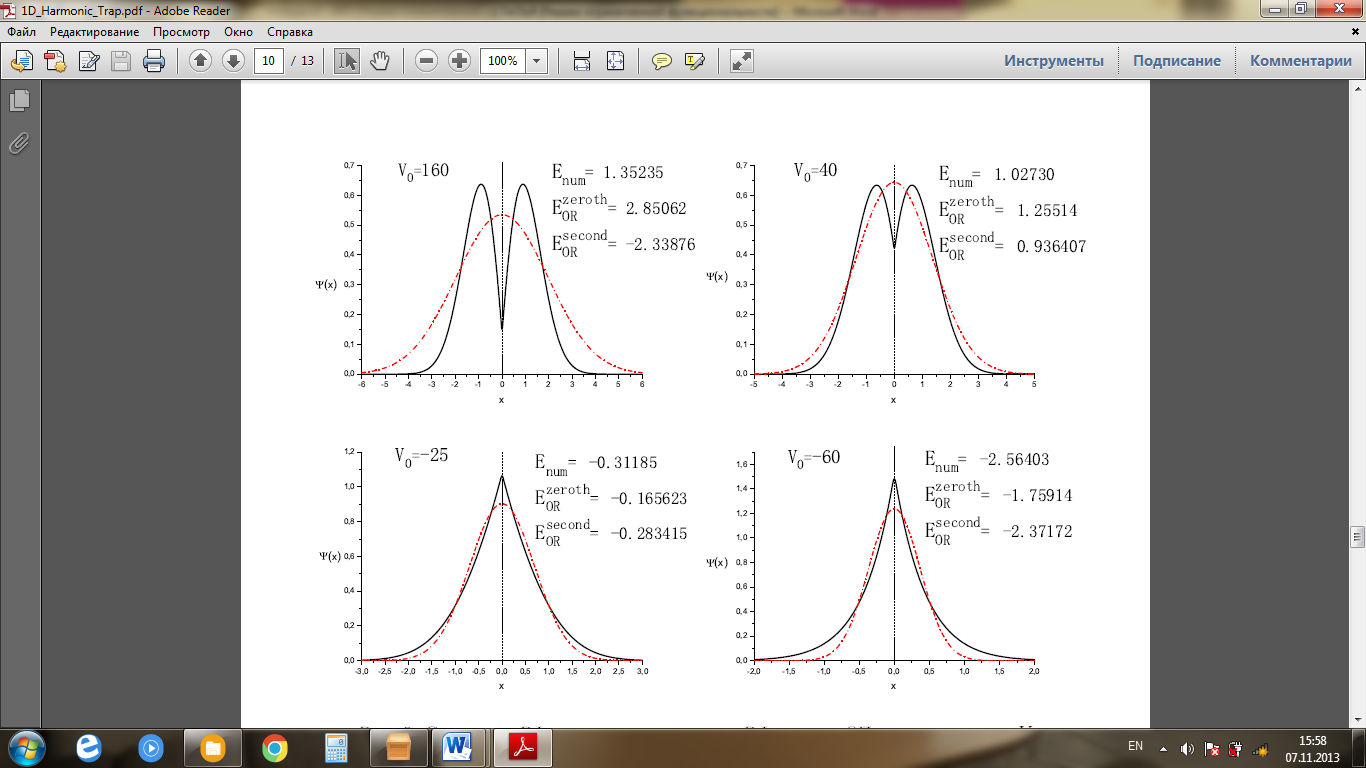
Тұтас сызықтар – сандық есептеудегі ТФ. Штрихпунктирлі сызықтар – ОӨ әдісіндегі нөлдік жуықтаудағы ТФ. 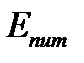 - энергияның сандық есептелуі,
- энергияның сандық есептелуі, 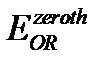 - ОӨ әдісіндегі нөлдік жуықтаудағы энергия,
- ОӨ әдісіндегі нөлдік жуықтаудағы энергия, 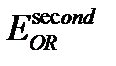 - ОӨ әдісіндегі екінші жуықтаудағы энергия.
- ОӨ әдісіндегі екінші жуықтаудағы энергия.
Сурет 6 – 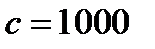 үшін әртүрлі
үшін әртүрлі 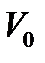 кезінде сандық есептеудегі ТФ мен ОӨ әдісіндегі ТФ салыстыру.
кезінде сандық есептеудегі ТФ мен ОӨ әдісіндегі ТФ салыстыру.
Тұтас сызықтар – сандық есептеудегі ТФ. Штрихпунктирлі сызықтар – ОӨ нөлдік жуықтаудағы ТФ. 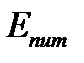 - энергияның сандық есептелуі,
- энергияның сандық есептелуі, 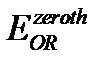 - ОӨ нөлдік жуықтаудағы энергия,
- ОӨ нөлдік жуықтаудағы энергия, 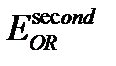 - ОӨ екінші жуықтаудағы энергия.
- ОӨ екінші жуықтаудағы энергия.
Сурет 7 – 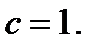 үшін әртүрлі
үшін әртүрлі 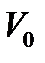 кезінде сандық есептеудегі ТФ мен ОӨ әдісіндегі ТФ салыстыру
кезінде сандық есептеудегі ТФ мен ОӨ әдісіндегі ТФ салыстыру
6,7-суреттерде көрініп тұрғандай, 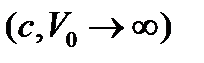 кезінде оң
кезінде оң 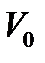 аймағында пайда болатын ОӨ әдісінің сандық есептеуден ауытқуы осы екі әдістің толқындық функцияларының ауырмашылығына сәйкес болады. Осылайша, (2.1) берілген гамильтониан үшін ОӨ әдісінің қолданылуы әсерлесу потенциалы параметрлерінің функциясы болып табылады.
аймағында пайда болатын ОӨ әдісінің сандық есептеуден ауытқуы осы екі әдістің толқындық функцияларының ауырмашылығына сәйкес болады. Осылайша, (2.1) берілген гамильтониан үшін ОӨ әдісінің қолданылуы әсерлесу потенциалы параметрлерінің функциясы болып табылады.
Бұл жұмыста бірөлшемді гармоникалық тұзақтағы екібозонды байланысқан жүйені сипаттайтын (2.1) ШТ негізгі күйінің энергиясы кері шашырау ұзындығының функциясы ретінде есептелді. Алынған 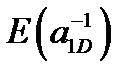 тәуелділік [21] жұмысындағы псевдопотенциалдық әдісте орындалған есептеуден бірқатар ерекшеленеді. Біздің жағдай Гаусстың реалистік потенциалын қолданумен ерекшеленеді, оны таңдау орынды болып табылады, өйткені ол атомдарда қандай да бір құрылымның бар екенін ескереді. Сондай-ақ соңғы радиус потенциалынан дельта-функция потенциалына ауысу айтарлықтай жуықтау болып табылады. Осыған ұқсас үшөлшемді реалистік потенциалмен және нөлдік радиустың псевдопотенциалымен орындалған есептеулердің салыстырылуы екіөлшемді гармоникалық тұзақ үшін [30] жұмысында келтірілген.
тәуелділік [21] жұмысындағы псевдопотенциалдық әдісте орындалған есептеуден бірқатар ерекшеленеді. Біздің жағдай Гаусстың реалистік потенциалын қолданумен ерекшеленеді, оны таңдау орынды болып табылады, өйткені ол атомдарда қандай да бір құрылымның бар екенін ескереді. Сондай-ақ соңғы радиус потенциалынан дельта-функция потенциалына ауысу айтарлықтай жуықтау болып табылады. Осыған ұқсас үшөлшемді реалистік потенциалмен және нөлдік радиустың псевдопотенциалымен орындалған есептеулердің салыстырылуы екіөлшемді гармоникалық тұзақ үшін [30] жұмысында келтірілген.
Осцилляторда өрнектелу әдісін әсерлесу потенциалы параметрлерінің функциясы ретінде қолданылу аймағы анықталды. ОӨ әдісінің сандық есептеуден ауытқуы осцилляторлық ТФ гаусстық түрінің шынайы ТФ түрінен ауытқуымен түсіндіріледі. ОӨ әдісінің қолданылу аймағын анықтау келешекте ангармоникалық тұзақтағы екіатомды жүйе спектрін есептеу кезінде қажет болады.
Ангармоникалық тұзақтағы екіатомдық жүйенің спектрін есептеу кезіндегі негізгі қиындық, бұл жағдайда салыстырмалы координата мен массалар орталығының координаталарының айнымалыларын бөлу мүмкін болмайды. Есептеуді альтернативті әдістермен жүргізу мүмкіндігі нәтижелердің сенімділігіне себепкер болады.
5.3 Исследование квазиодномерной трехатомной системы в гармонической ловушке
Разрабатываемый подход применим к задаче о трех одинаковых атомах в двумерной гармонической ловушке (квазиодномерная трехатомная система в гармонической ловушке), описываемой гамильтонианом
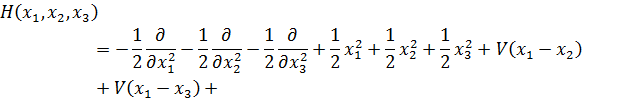
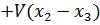 (5.3.1)
(5.3.1)
где в выборе потенциала взаимодействия между атомами V допускается достаточно широкий произвол. Гамильтониан записан в единицах 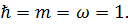 Эта задача допускает отделение движения ценра масс.
Эта задача допускает отделение движения ценра масс.
Действительно, при переходе к координатамЯкоби
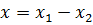
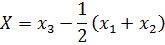
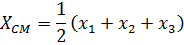
центр масс 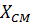 отделяется, а задача сводится к решению двумерного уравнения Шредингера
отделяется, а задача сводится к решению двумерного уравнения Шредингера
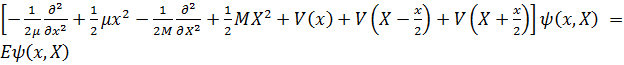 (5.3.2)
(5.3.2)
где 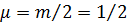 приведенная масса двух атомов, а
приведенная масса двух атомов, а
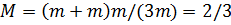 приведенная масса трех атомов. К этому уравнению мы планируем применить разрабатываемый подход (см. предыдущие параграфы этого раздела). Задача (
приведенная масса трех атомов. К этому уравнению мы планируем применить разрабатываемый подход (см. предыдущие параграфы этого раздела). Задача ( 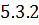 ) актуальна в связи с работами по экспериментальному исследованию резонансов Ефимова в атомных ловушках. После отработки метода на решении задач обсуждаемых в параграфах 6.1 и 6.2 мы планируем его применение для численного решения 2D уравнения Шредингера (
) актуальна в связи с работами по экспериментальному исследованию резонансов Ефимова в атомных ловушках. После отработки метода на решении задач обсуждаемых в параграфах 6.1 и 6.2 мы планируем его применение для численного решения 2D уравнения Шредингера ( 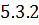 ) с реалистичнымимежатомными взаимодействиями V и исследования условий возникновения резонансов Ефимова в квазиодномерных атомных системах в гармонических ловушках.
) с реалистичнымимежатомными взаимодействиями V и исследования условий возникновения резонансов Ефимова в квазиодномерных атомных системах в гармонических ловушках.
3 ЭНЕРГЕТИЧЕСКИЙ СПЕКТР ГАРМОНИЧЕСКОЙ ЛОВУШКИ ДВУХАТОМНЫХ МОЛЕКУЛ
3.1 Спектр для одномерной оптической ловушки
Сначала исследуем спектр более простого (одномерного) гамильтониана
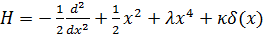 (3.1)
(3.1)
по схеме изложенной в главе 1. Здесь 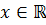 , а λ и
, а λ и 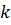 – некоторые параметры, а в точке максимума
– некоторые параметры, а в точке максимума 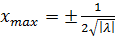 потенциального барьера
потенциального барьера 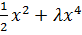 , при
, при 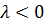 , ставится бесконечная стенка.
, ставится бесконечная стенка.
Оценим также и первый порядок теории возмущений для задачи (3.1). Здесь поправка к энергии имеет более простой вид и энергия в первом порядке теории возмущений определяется как:
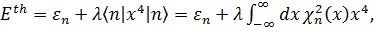 (3.2)
(3.2)
где 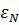 и
и 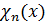 определяются из (1.29) и (1.30), однако, для параметра
определяются из (1.29) и (1.30), однако, для параметра 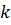 вместо
вместо 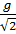 .
.
В эксперименте [2] была реализована квази-одномерная геометрия, где также оценивалась формула из работы [18]. Исследование в [2,19] проводилось в области значений 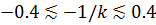 для основного состояния и первого четного возбужденного состояния
для основного состояния и первого четного возбужденного состояния 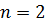 . К решениям для этих состояний мы добавили результаты для второго четного возбужденного состояния
. К решениям для этих состояний мы добавили результаты для второго четного возбужденного состояния 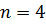 . Область отрицательных значений
. Область отрицательных значений 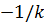 соответствует состояниям
соответствует состояниям 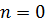 и
и 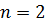 , а область положительных значений
, а область положительных значений 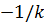 – состояниям
– состояниям 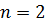 и
и 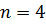 . Результаты представлены на рисунке 8.Сплошные линии относятся к численному расчету спектра, пунктирные – к расчету по теории возмущений по формуле (3.2). Синие кривые относятся к λ
. Результаты представлены на рисунке 8.Сплошные линии относятся к численному расчету спектра, пунктирные – к расчету по теории возмущений по формуле (3.2). Синие кривые относятся к λ 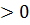 , красные – к λ
, красные – к λ 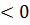 . Линия с названием «барьер» указывает границу энергии, выше которой энергия уровня начинает превышать потенциальный барьер
. Линия с названием «барьер» указывает границу энергии, выше которой энергия уровня начинает превышать потенциальный барьер 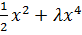 .
.
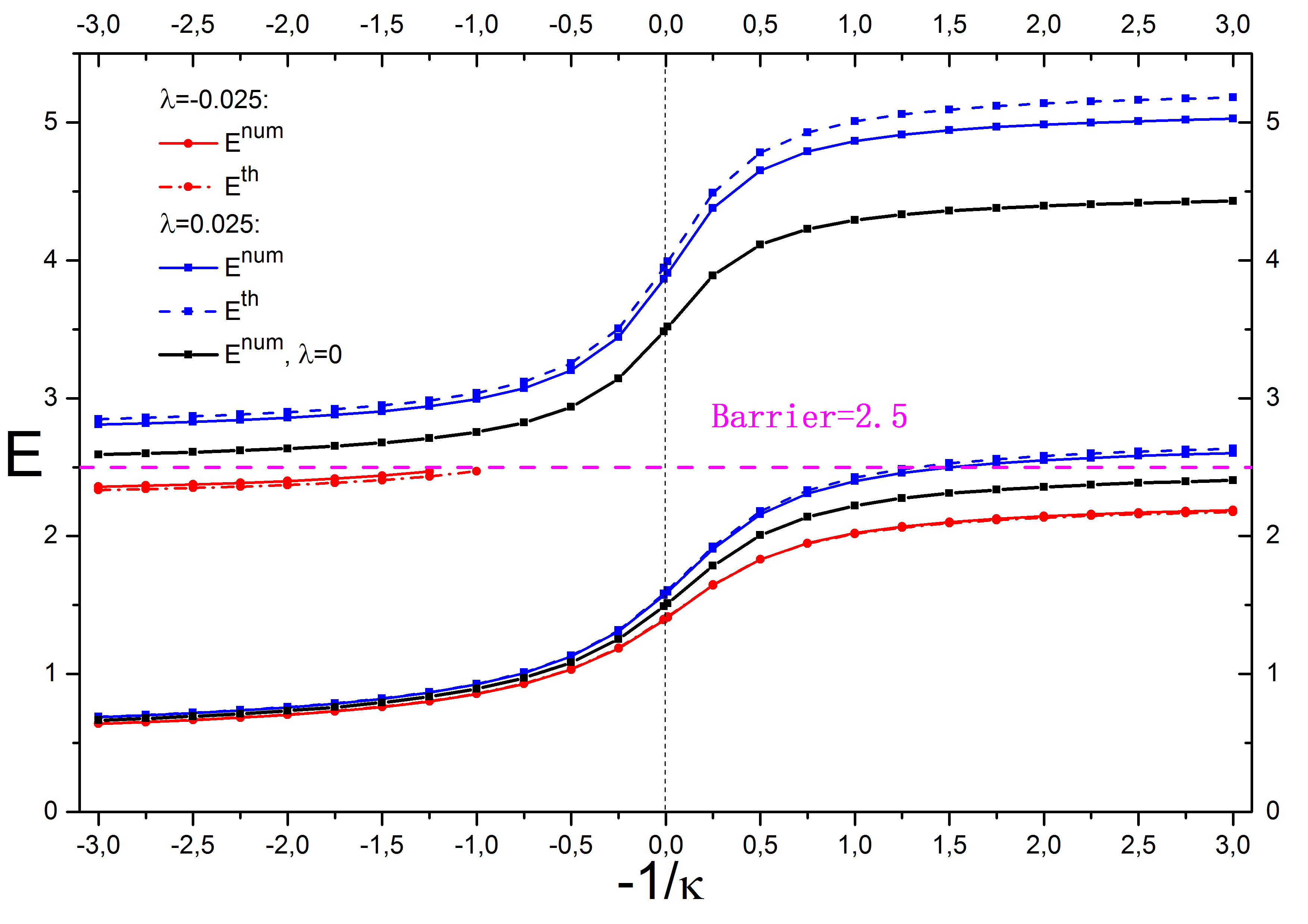
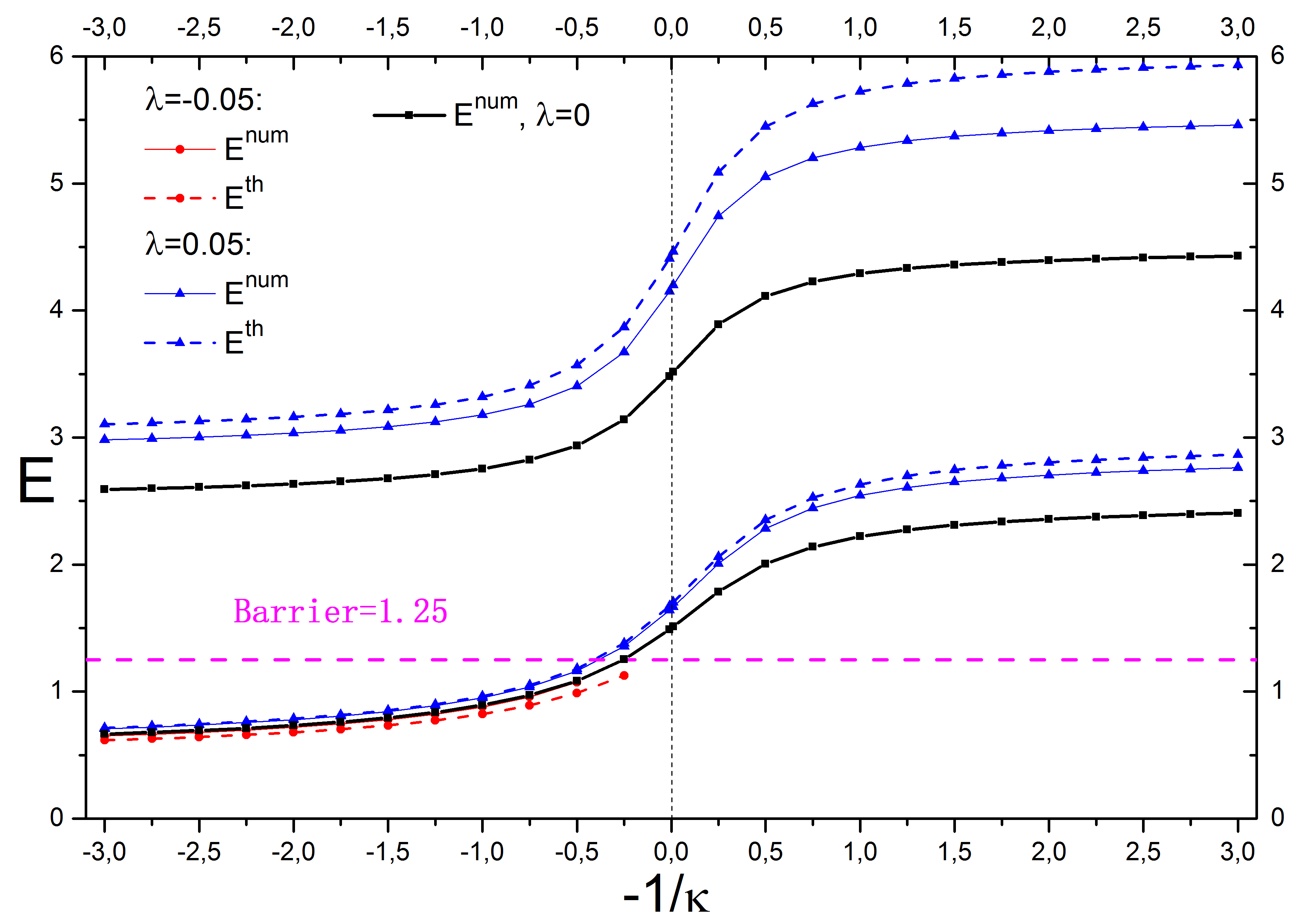
Рисунок 8 -Энергетический спектр гамильтониана (3.1)
При λ 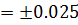 , для низших состояний, обнаруживается хорошее согласие численного решения и решения, полученного методом теории возмущений. При λ
, для низших состояний, обнаруживается хорошее согласие численного решения и решения, полученного методом теории возмущений. При λ 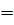 -0.05, значительное отклонение двух решений (кривая численного решения практически сливается с решением при λ
-0.05, значительное отклонение двух решений (кривая численного решения практически сливается с решением при λ 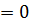 ) можно объяснить тем, что уровень энергии приближается к вершине потенциального барьера
) можно объяснить тем, что уровень энергии приближается к вершине потенциального барьера 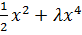 , где начинает сильно проявляться наличие бесконечной стенки.
, где начинает сильно проявляться наличие бесконечной стенки.
3.2 Двумерная гармоническая ловушка
На рисунке 9 представлены результаты решения уравнения (1.10), полученные двумя методами – численным, с потенциалами 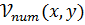 и
и 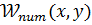 , а также по теории возмущений с потенциалом (1.7). Также на этом же графике представлены результаты расчетов для случая двумерной гармонической ловушки, т.е. решения уравнения (1.10)при
, а также по теории возмущений с потенциалом (1.7). Также на этом же графике представлены результаты расчетов для случая двумерной гармонической ловушки, т.е. решения уравнения (1.10)при 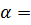 0.
0.
Ограниченность спектров на рисунке 9, при 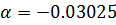 и
и 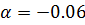 , в отрицательной области 1/
, в отрицательной области 1/ 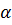 , обусловлена тем, что здесь уровни энергии достигают барьера потециала
, обусловлена тем, что здесь уровни энергии достигают барьера потециала 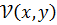 .
.
Здесь также представлены расчеты при положительных 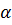 , для сравнения с теорией возмущений. При отрицательных
, для сравнения с теорией возмущений. При отрицательных 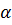 ситуация подобна одномерному случаю, когда разница численного решения и решения по теории возмущений увеличивается, что также можно объяснить приближением энергии уровня, рассчитанной численным методом [20], к вершине потенциального барьера.
ситуация подобна одномерному случаю, когда разница численного решения и решения по теории возмущений увеличивается, что также можно объяснить приближением энергии уровня, рассчитанной численным методом [20], к вершине потенциального барьера.
Рассчитанные спектры представлены в зависимости от обратной длины рассеяния 1/ 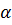 :
:
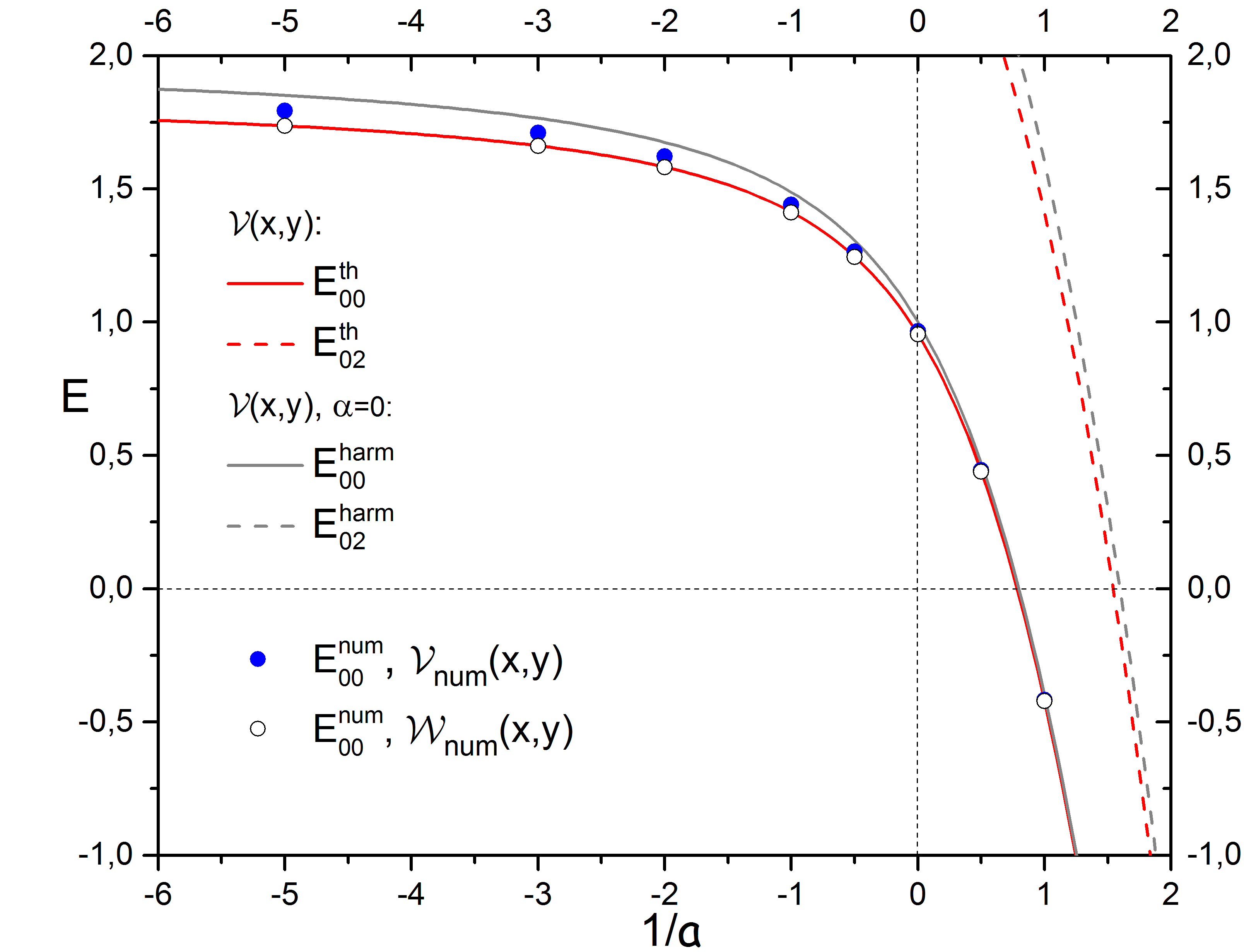
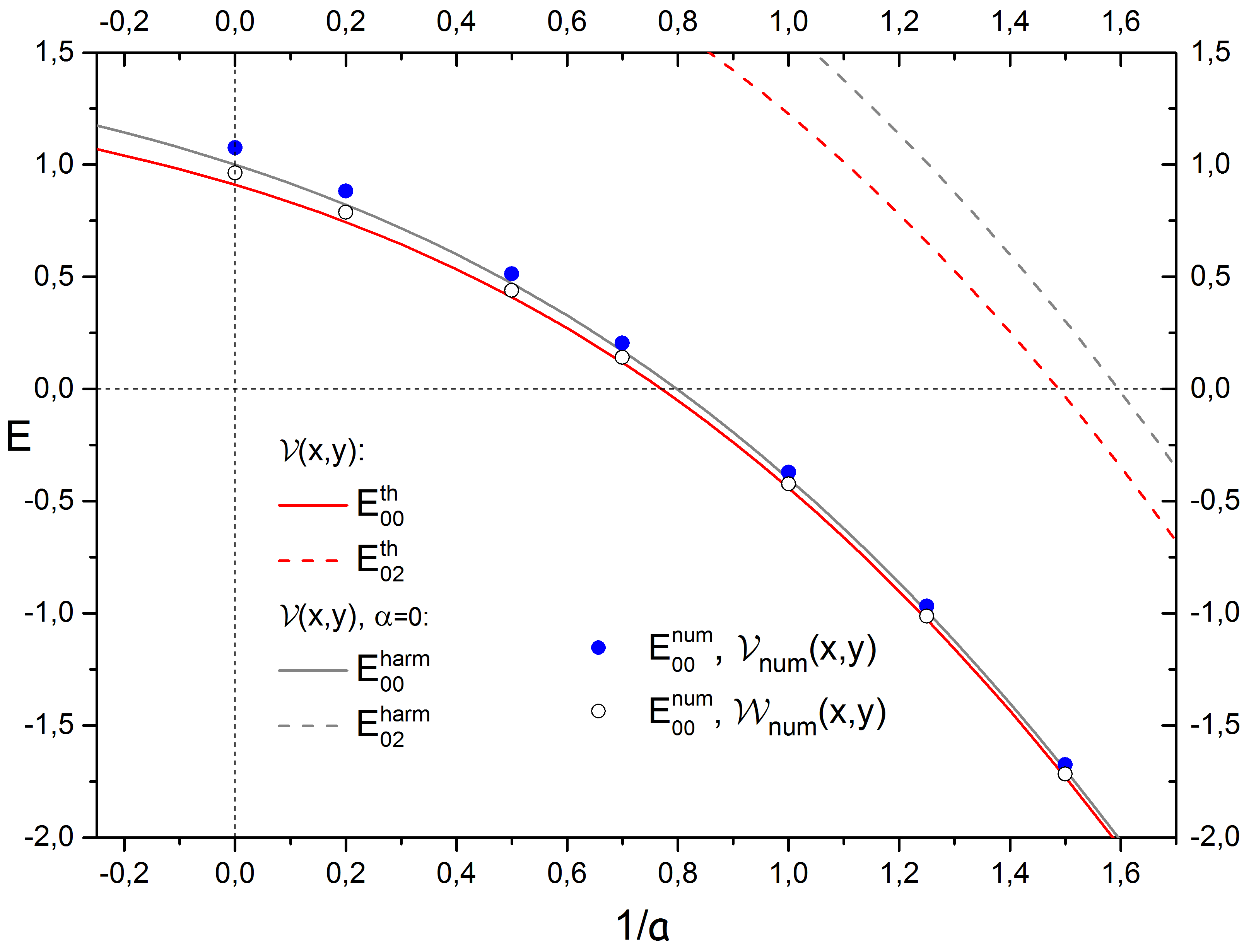
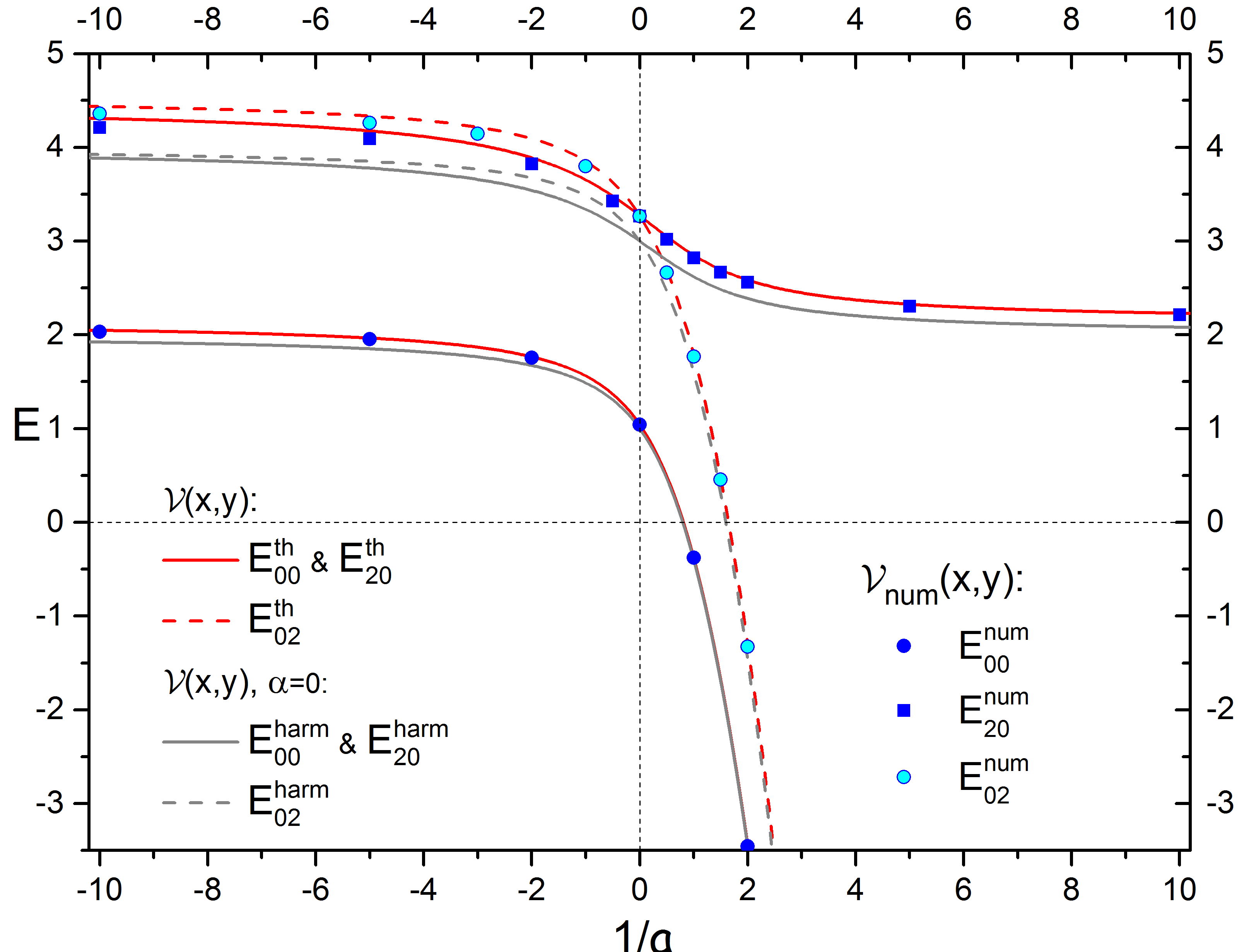
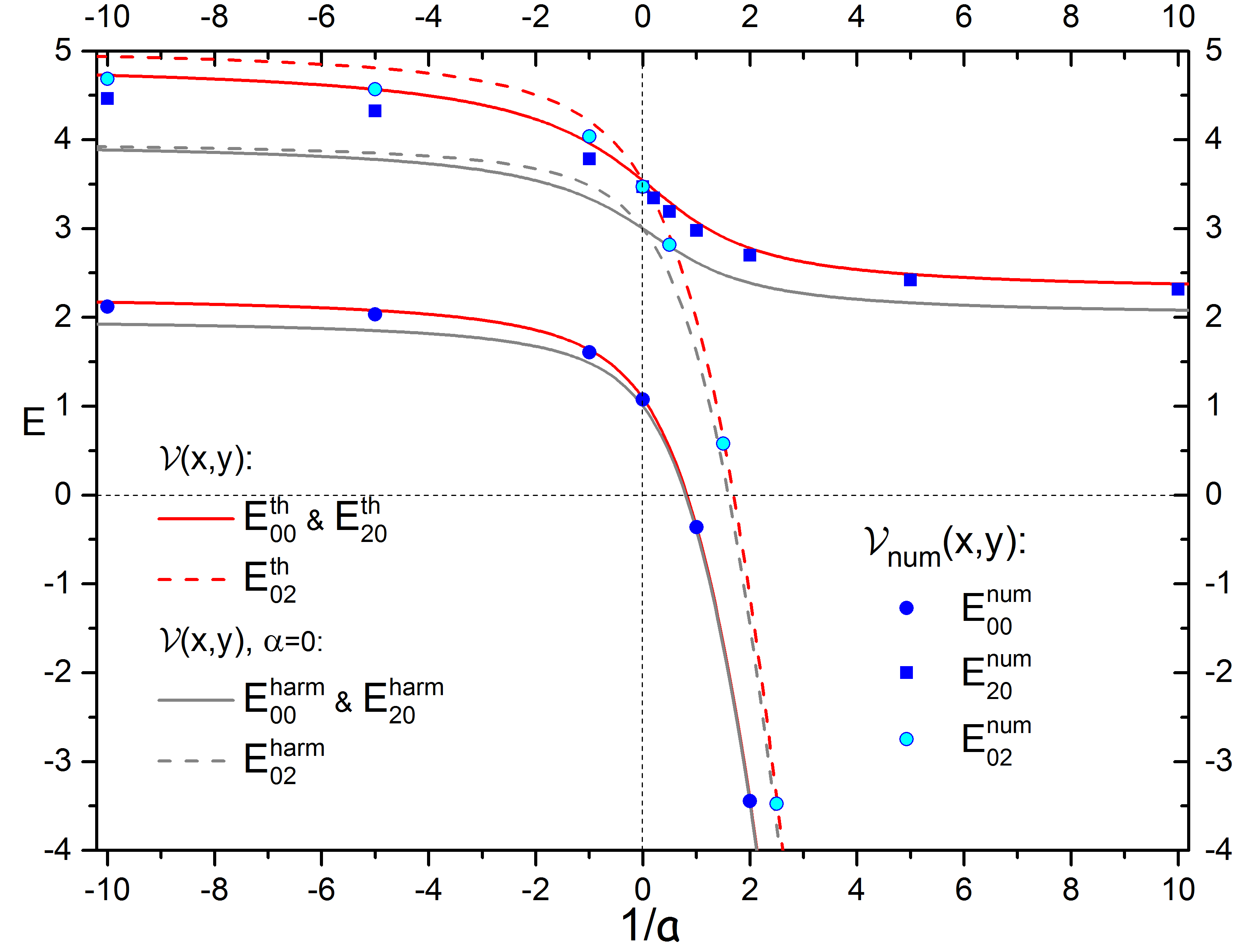
Синими и голубыми точками показаны численные расчеты для потенциала 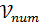 , открытые белые точки – для потенциала
, открытые белые точки – для потенциала 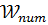 ; Серыми линиями показаны расчеты
; Серыми линиями показаны расчеты 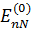 из (1.27), красными – решения первого порядка теории возмущений (1.33) и (1.34).
из (1.27), красными – решения первого порядка теории возмущений (1.33) и (1.34).
Рисунок 9 - Энергетический спектр гамильтониана (1.6) для трех состояний:
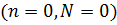 ,
, 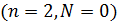 и
и 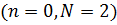 .
.
3.3 Оценка сходимости теории возмущений
Оценим сходимость теории возмущений по критерию:
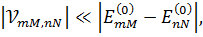 (3.3)
(3.3)
где матричные элементы 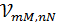 равны:
равны:
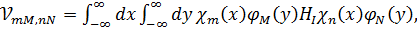 (3.4)
(3.4)
а энергия в нулевом порядке теории возмущений 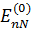 равна:
равна:
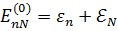 (3.5)
(3.5)
Для оценки (3.3) рассмотрим лишь комбинации с двумя четными нижним уровнями. Это даст хотя и не строгий, но более-менее качественный критерий применимости теории. Таким образом, оценим матричные элементы 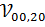 ,
, 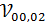 ,
, 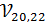 и
и 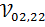 , которые равны:
, которые равны:
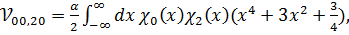 (3.6)
(3.6)
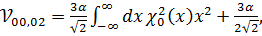 (3.7)
(3.7)
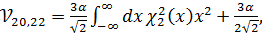 (3.8)
(3.8)
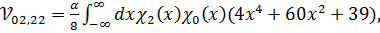 (3.9)
(3.9)
Для оценки сходимости теории возмущений матричных элементов (3.6)- (3.9) рассмотрим следующие величины:
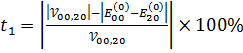 (3.10)
(3.10)
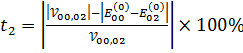 (3.11)
(3.11)
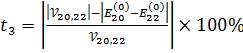 (3.12)
(3.12)
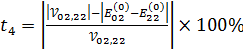 (3.13)
(3.13)
Результаты расчетов оценок (3.10)- (3.13), в зависимости от обратной длины рассеяния, представлены на рисунке 10:
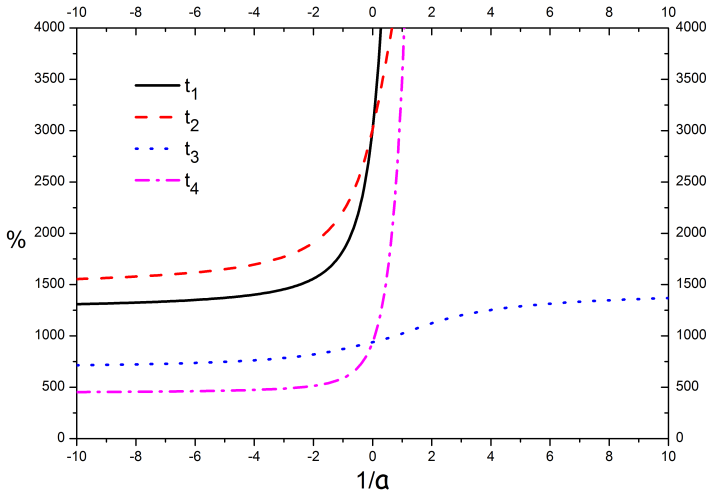
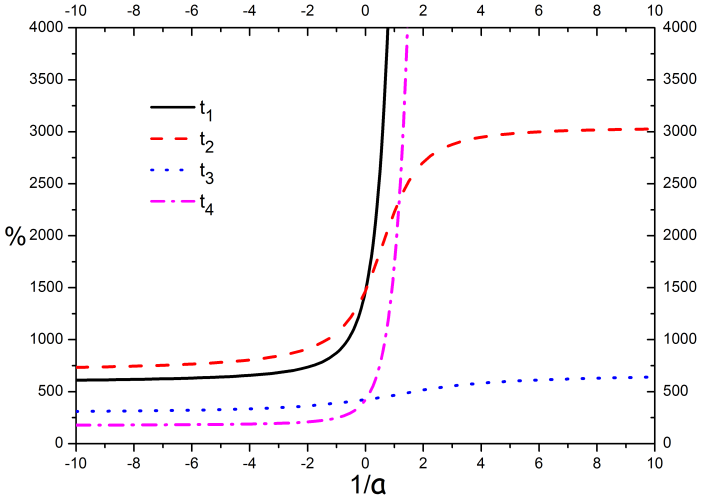
Рисунок 10 - Оценка области сходимости теории возмущений
Из графиков видно, что при значениях 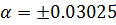 величины (3.10)-(3.13) имеют большие значения в сравнении со случаями
величины (3.10)-(3.13) имеют большие значения в сравнении со случаями 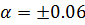 , что говорит о приемлемости метода, при малых
, что говорит о приемлемости метода, при малых 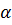 . Эта ситуация также наблюдается и на рисунке 5, где видно хорошее согласие теории возмущений с численным решением при
. Эта ситуация также наблюдается и на рисунке 5, где видно хорошее согласие теории возмущений с численным решением при 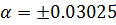 .
.
3 ЭНЕРГЕТИЧЕСКИЙ СПЕКТР ГАРМОНИЧЕСКОЙ ЛОВУШКИ ДВУХАТОМНЫХ МОЛЕКУЛ
3.1 Спектр для одномерной оптической ловушки
Сначала исследуем спектр более простого (одномерного) гамильтониана
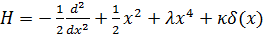 (3.1)
(3.1)
по схеме изложенной в главе 1. Здесь 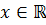 , а λ и
, а λ и 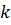 – некоторые параметры, а в точке максимума
– некоторые параметры, а в точке максимума 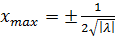 потенциального барьера
потенциального барьера 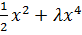 , при
, при 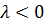 , ставится бесконечная стенка.
, ставится бесконечная стенка.
Оценим также и первый порядок теории возмущений для задачи (3.1). Здесь поправка к энергии имеет более простой вид и энергия в первом порядке теории возмущений определяется как:
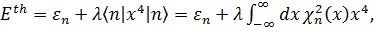 (3.2)
(3.2)
где 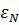 и
и 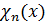 определяются из (1.29) и (1.30), однако, для параметра
определяются из (1.29) и (1.30), однако, для параметра 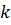 вместо
вместо 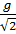 .
.
В эксперименте [2] была реализована квази-одномерная геометрия, где также оценивалась формула из работы [18]. Исследование в [2,19] проводилось в области значений 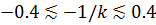 для основного состояния и первого четного возбужденного состояния
для основного состояния и первого четного возбужденного состояния 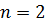 . К решениям для этих состояний мы добавили результаты для второго четного возбужденного состояния
. К решениям для этих состояний мы добавили результаты для второго четного возбужденного состояния 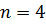 . Область отрицательных значений
. Область отрицательных значений 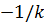 соответствует состояниям
соответствует состояниям 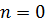 и
и 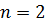 , а область положительных значений
, а область положительных значений 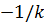 – состояниям
– состояниям 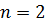 и
и 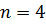 . Результаты представлены на рисунке 8.Сплошные линии относятся к численному расчету спектра, пунктирные – к расчету по теории возмущений по формуле (3.2). Синие кривые относятся к λ
. Результаты представлены на рисунке 8.Сплошные линии относятся к численному расчету спектра, пунктирные – к расчету по теории возмущений по формуле (3.2). Синие кривые относятся к λ 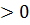 , красные – к λ
, красные – к λ 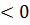 . Линия с названием «барьер» указывает границу энергии, выше которой энергия уровня начинает превышать потенциальный барьер
. Линия с названием «барьер» указывает границу энергии, выше которой энергия уровня начинает превышать потенциальный барьер 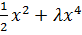 .
.


Рисунок 8 -Энергетический спектр гамильтониана (3.1)
При λ 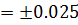 , для низших состояний, обнаруживается хорошее согласие численного решения и решения, полученного методом теории возмущений. При λ
, для низших состояний, обнаруживается хорошее согласие численного решения и решения, полученного методом теории возмущений. При λ 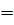 -0.05, значительное отклонение двух решений (кривая численного решения практически сливается с решением при λ
-0.05, значительное отклонение двух решений (кривая численного решения практически сливается с решением при λ 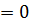 ) можно объяснить тем, что уровень энергии приближается к вершине потенциального барьера
) можно объяснить тем, что уровень энергии приближается к вершине потенциального барьера 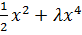 , где начинает сильно проявляться наличие бесконечной стенки.
, где начинает сильно проявляться наличие бесконечной стенки.
3.2 Двумерная гармоническая ловушка
На рисунке 9 представлены результаты решения уравнения (1.10), полученные двумя методами – численным, с потенциалами 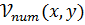 и
и 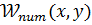 , а также по теории возмущений с потенциалом (1.7). Также на этом же графике представлены результаты расчетов для случая двумерной гармонической ловушки, т.е. решения уравнения (1.10)при
, а также по теории возмущений с потенциалом (1.7). Также на этом же графике представлены результаты расчетов для случая двумерной гармонической ловушки, т.е. решения уравнения (1.10)при 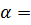 0.
0.
Ограниченность спектров на рисунке 9, при 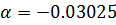 и
и 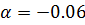 , в отрицательной области 1/
, в отрицательной области 1/ 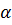 , обусловлена тем, что здесь уровни энергии достигают барьера потециала
, обусловлена тем, что здесь уровни энергии достигают барьера потециала 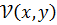 .
.
Здесь также представлены расчеты при положительных 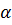 , для сравнения с теорией возмущений. При отрицательных
, для сравнения с теорией возмущений. При отрицательных 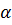 ситуация подобна одномерному случаю, когда разница численного решения и решения по теории возмущений увеличивается, что также можно объяснить приближением энергии уровня, рассчитанной численным методом [20], к вершине потенциального барьера.
ситуация подобна одномерному случаю, когда разница численного решения и решения по теории возмущений увеличивается, что также можно объяснить приближением энергии уровня, рассчитанной численным методом [20], к вершине потенциального барьера.
Рассчитанные спектры представлены в зависимости от обратной длины рассеяния 1/ 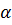 :
:




Синими и голубыми точками показаны численные расчеты для потенциала 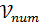 , открытые белые точки – для потенциала
, открытые белые точки – для потенциала 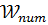 ; Серыми линиями показаны расчеты
; Серыми линиями показаны расчеты 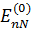 из (1.27), красными – решения первого порядка теории возмущений (1.33) и (1.34).
из (1.27), красными – решения первого порядка теории возмущений (1.33) и (1.34).
Рисунок 9 - Энергетический спектр гамильтониана (1.6) для трех состояний:
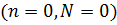 ,
, 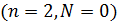 и
и 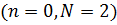 .
.
3.3 Оценка сходимости теории возмущений
Оценим сходимость теории возмущений по критерию:
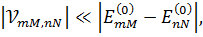 (3.3)
(3.3)
где матричные элементы 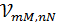 равны:
равны:
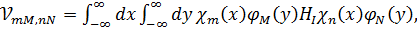 (3.4)
(3.4)
а энергия в нулевом порядке теории возмущений 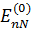 равна:
равна:
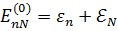 (3.5)
(3.5)
Для оценки (3.3) рассмотрим лишь комбинации с двумя четными нижним уровнями. Это даст хотя и не строгий, но более-менее качественный критерий применимости теории. Таким образом, оценим матричные элементы 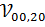 ,
, 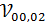 ,
, 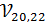 и
и 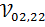 , которые равны:
, которые равны:
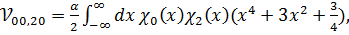 (3.6)
(3.6)
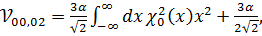 (3.7)
(3.7)
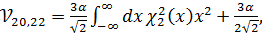 (3.8)
(3.8)
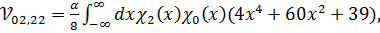 (3.9)
(3.9)
Для оценки сходимости теории возмущений матричных элементов (3.6)- (3.9) рассмотрим следующие величины:
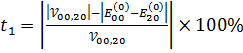 (3.10)
(3.10)
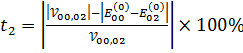 (3.11)
(3.11)
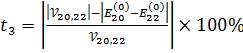 (3.12)
(3.12)
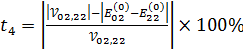 (3.13)
(3.13)
Результаты расчетов оценок (3.10)- (3.13), в зависимости от обратной длины рассеяния, представлены на рисунке 10:


Рисунок 10 - Оценка области сходимости теории возмущений
Из графиков видно, что при значениях 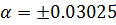 величины (3.10)-(3.13) имеют большие значения в сравнении со случаями
величины (3.10)-(3.13) имеют большие значения в сравнении со случаями 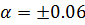 , что говорит о приемлемости метода, при малых
, что говорит о приемлемости метода, при малых 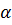 . Эта ситуация также наблюдается и на рисунке 5, где видно хорошее согласие теории возмущений с численным решением при
. Эта ситуация также наблюдается и на рисунке 5, где видно хорошее согласие теории возмущений с численным решением при 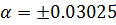 .
.
