ЗАНЯТИЕ 2. Однородные функции и однородные уравнения первого порядка. Уравнения специального вида, приводящиеся к однородному ДУ 1-го порядка.
| Ауд. | Л-3 | гл.10: № 47, 50, 55, 56, 59, 60, 62, 177. |
☺ ☻ ☺
Пример 1–47: Решить дифференциальное уравнение: y′ =  + sin
+ sin  .
.
Решение:
1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
2). Данное уравнение решаем, применяя общий алгоритм «А» (см. Лекцию!):
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0. Это даёт одно из решений: y = y0 – прямая, параллельная оси ОХ.
a2. Примем  = u; получим выражение: φ(u)=f(u)–u.
= u; получим выражение: φ(u)=f(u)–u.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Если оно выполняется, то одним из решений заданного уравнения является прямая: u=u0 , или прямая y=u0 x.
a4. Учитывая, что теперь f(u)–u≠0, запишем ДУ в виде: 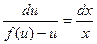 . (1)
. (1)
a5. Находим интеграл: J= 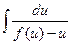 .
.
a6. Записываем результат интегрирования уравнения (1): J=lnCx. Записываем общее решение ДУ, учитывая что u =  .
.
3). В нашем случае:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0. Это даёт одно из решений: y = y0 =0 – ось ОХ.
a2. Примем  = u; получим: φ(u)=f(u)–u= u+ sinu–u= sinu.
= u; получим: φ(u)=f(u)–u= u+ sinu–u= sinu.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. У нас: sinu = 0 даёт u=u0 =πn, n  Z, которые являются решениями ДУ, то есть y=x∙πn, n
Z, которые являются решениями ДУ, то есть y=x∙πn, n  Z – семейство прямых, проходящих через начало координат XOY. При n=0 получаем найденное ранее y0 =0 – ось ОХ.
Z – семейство прямых, проходящих через начало координат XOY. При n=0 получаем найденное ранее y0 =0 – ось ОХ.
a4. Учитывая, что теперь f(u)–u≠0, запишем ДУ в виде (1): 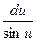 =
= 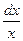 .
.
a5. Интегрируем уравнение (1): ln|tg 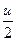 |= lnCx → tg
|= lnCx → tg 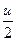 =Cх.
=Cх.
a6. Записываем общее решение ДУ. Учитывая что 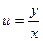 , получаем: tg
, получаем: tg 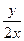 = Cх.
= Cх.
Ответ: tg 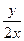 = Cх – общее решение ДУ, также: y = x∙πn, n
= Cх – общее решение ДУ, также: y = x∙πn, n  Z.
Z.
Пример 2–50: Решить дифференциальное уравнение: (x–y)dx+xdy =0.
Решение:
1). Заданное ДУ – однородное: множители при dx и dy – однородные функции 1-го порядка (одинакового!). Далее используется «стандартный алгоритм» решения уравнения, заданного в дифференциальной форме.
2). Данное уравнение решаем, применяя общий алгоритм «В» (см. Лекцию!):
a0. Выделяем возможные решения исходного уравнения f1(x,y)dx+f2(x,y)dy=0. Первое: f1(x,y0)=0. Это даёт одно из решений: y=y0 – прямая, параллельная оси ОХ. Второе: f2(x0,y)=0. Это даёт ещё одно из решений: x=x 0 – прямая, параллельная оси ОY.
a1. Для заданного уравнения: f1(x,y)dx+f2(x,y)dy = 0 запишем очевидное преобразование: y′= 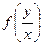 , где
, где 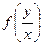 =
= 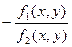 , где правая часть является однородной функцией нулевого порядка, так как f1(x,y) и f2(x,y)–однородные функции одного порядка. Здесь учтено: f2(x,y) ≠ 0.
, где правая часть является однородной функцией нулевого порядка, так как f1(x,y) и f2(x,y)–однородные функции одного порядка. Здесь учтено: f2(x,y) ≠ 0.
a2. Примем  = u; получим выражение: φ(u)=f(u)–u.
= u; получим выражение: φ(u)=f(u)–u.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Если оно выполняется, то одним из решений заданного уравнения является прямая: u=u0 , или прямая y=u0 x.
a4. Учитывая, что теперь f(u)–u≠0, запишем ДУ в виде: 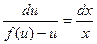 . (1)
. (1)
a5. Находим интеграл: J= 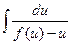 .
.
a6. Записываем результат интегрирования уравнения (1): J=lnCx. Записываем общее решение ДУ, учитывая что u =  .
.
3). В нашем случае ДУ: (x–y)dx+xdy =0.
a0. Выделяем возможные решения исходного уравнения f1(x,y)dx+f2(x,y)dy=0.Имеем: f1(x,y)= (x–y); f2(x,y) = x. Первое: f1(x,y0) ≠0 ни при каких y0, так как x может принимать произвольные значения! Второе условие: f2(x0,y)=0. Даёт решение: x=x0=0– ось ОY.
a1. Запишем наше уравнение в виде: y′= 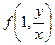 : y′=
: y′=  –1. Здесь учтено: f2(x,y)=x≠ 0.
–1. Здесь учтено: f2(x,y)=x≠ 0.
a2. Примем  = u; получим выражение: φ(u)=f(u)–u=u–1–u= –1.
= u; получим выражение: φ(u)=f(u)–u=u–1–u= –1.
a3. Проверим условие: φ(u0)=–1≠0.
a4. Учитывая, что теперь f(u)–u≠0, записываем уравнение: 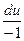 =
= 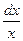 . (1)
. (1)
a5. Находим интеграл: J= 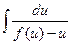 =–u.
=–u.
a6. Записываем результат интегрирования уравнения (1): –u=lnCx → e–u =Cх. Записываем общее решение ДУ. Учитывая что u =  , получаем: x∙
, получаем: x∙ 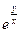 =C.
=C.
Ответ: x∙ 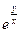 =C – общее решение ДУ, также x=0 (из общего не выделяется ни при каком С).
=C – общее решение ДУ, также x=0 (из общего не выделяется ни при каком С).
Пример 3–55: Решить дифференциальное уравнение: xy′– y = 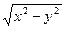 .
.
Решение:
Замечание: так как переменная может принимать как значения x>0, так и x<0, необходимо рассмотреть оба случая!
Случай-1–x>0:
0). Представим ДУ в виде: y′ =  +
+ 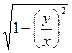 . Деление на x≠0.
. Деление на x≠0.
1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
2). Данное уравнение решаем, применяя общий алгоритм «А»:
3). В нашем случае:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0. Их нет.
a2. Примем  = u; получим: φ(u)=f(u)–u=u+
= u; получим: φ(u)=f(u)–u=u+ 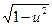 –u=
–u= 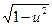 .
.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Следует: u0= ±1, или y= ±x.
a4. Учитывая, что теперь f(u)–u≠0, запишем ДУ в виде (1): 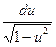 =
= 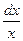 .
.
a5. Интегрируем уравнение (1): arcsinu=ln|x|+C, или u=sin(ln|x|+C).
a6. Записываем общее решение. Учитывая что u=  , получаем: y=xsin(ln|x|+C).
, получаем: y=xsin(ln|x|+C).
Ответ: y=xsin(ln|x|+C) – общее решение ДУ, также y= ±x (из общего не выделяется).
Случай-2–x<0:
0). Представим ДУ в виде: y′ =  –
– 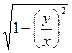 . Деление на x≠0.
. Деление на x≠0.
1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
2). Данное уравнение решаем, применяя общий алгоритм «А»:
3). В нашем случае:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0. Их нет.
a2. Примем  = u; получим: φ(u)=f(u)–u=u–
= u; получим: φ(u)=f(u)–u=u– 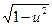 –u= –
–u= – 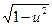 .
.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Следует: u0= ±1, или y= ±x.
a4. Учитывая, что теперь f(u)–u≠0, запишем ДУ в виде (1): – 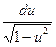 =
= 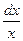 .
.
a5. Интегрируем уравнение (1): –arcsinu=ln|x|+C, или u=–sin(ln|x|+C).
a6. Записываем общее решение. Учитывая что u=  , получаем: y=–xsin(ln|x|+C).
, получаем: y=–xsin(ln|x|+C).
Ответ: y=–xsin(ln|x|+C) – общее решение ДУ, также y= ±x (из общего не выделяется).
Замечание: многие Случай-2 не выделяют (в шахматах это называют «зевок»!).
Пример 4–56: Решить дифференциальное уравнение: (x2 +y2)dy–2xydx=0.
Решение:
1). Признак, что задано однородное уравнение: множители при dx и dy – однородные функции 2-го порядка (одинакового!). Воспользуемся «стандартной схемой» решения.
2). Данное уравнение решаем, применяя общий алгоритм «В» (см. 2-50):
3). В нашем случае ДУ: (x2+y2)dy–2xydx=0.
a0. Выделяем возможные решения исходного уравнения f1(x,y)dx+f2(x,y)dy=0. Имеем: f1(x,y)= –2yx; f2(x,y)=(x2+y2). Первое дает решение: f1(x,y0)=0 при y0=0 – ось ОХ. Второе: f2(x0,y)=(x2+y2)≠0 при произвольных переменных!
a1. Запишем наше уравнение в виде: y′= 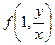 =
= 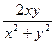 =
= 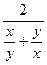 . Здесь теперь учтено: f2(x,y)= (x2+y2) ≠ 0 и x,y≠ 0.
. Здесь теперь учтено: f2(x,y)= (x2+y2) ≠ 0 и x,y≠ 0.
a2. Примем  = u; получим выражение: φ(u)=f(u)–u=–
= u; получим выражение: φ(u)=f(u)–u=– 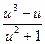 .
.
a3. Так как x,y≠ 0, то φ(u)≠0.
a4. Учитывая, что теперь f(u)–u≠0, записываем уравнение: – 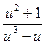 =
= 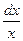 . (1)
. (1)
a5. Находим интеграл: J=– 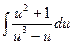 → трудоемкий процесс!
→ трудоемкий процесс!
Так как исходная запись ДУ симметрична относительно переменных, то станем искать решение ДУ в виде функции: x=x(y). Алгоритм решения остаётся (с точностью до обозначений) прежним!
a1. Запишем наше уравнение в виде: x′= 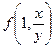 =
= 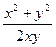 =
= 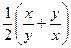 . Здесь теперь учтено: x,y≠ 0.
. Здесь теперь учтено: x,y≠ 0.
a2. Примем 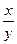 = u; получим выражение: φ(u)=f(u)–u=–
= u; получим выражение: φ(u)=f(u)–u=– 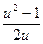 .
.
a3. Проверим условие: φ(u0)=0. Имеем u0=±1, то есть y =± x – тоже решения.
a4. Учитывая, что теперь f(u)–u≠0, записываем уравнение: – 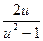 =
= 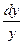 . (1)
. (1)
a5. Находим интеграл: J=– 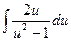 =–ln|u2–1|.
=–ln|u2–1|.
a6. Результат интегрирования уравнения (1): –ln|u2–1|=lnCy → (u2–1)y=C. Записываем общее решение ДУ. Учитывая что u = 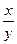 , получаем: y2– x2 =Cy.
, получаем: y2– x2 =Cy.
Ответ: y2– x2 =Cy – общее решение ДУ, также y =± x (выделяется из общего при С=0).
Пример 5–59: Решить дифференциальное уравнение: (y+2)dx–(2x+y–4)dy =0.
Решение:
1). Заданное ДУ – специального вида: множители при dx и dy – линейные функции, их отношение образует специальную дробь: 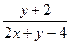 . Так как прямые l1: 0x+y+2=0 и l2:2x+y–4=0 пересекаются: их нормальные векторы
. Так как прямые l1: 0x+y+2=0 и l2:2x+y–4=0 пересекаются: их нормальные векторы 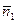 =(0,1) и
=(0,1) и 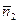 =(2,1) не коллинеарны, то имеем Случай-1 уравнения специального вида. Далее используется «стандартный алгоритм» для этого случая.
=(2,1) не коллинеарны, то имеем Случай-1 уравнения специального вида. Далее используется «стандартный алгоритм» для этого случая.
2). Данное уравнение решаем, применяя алгоритм «Случай-1» (см. Лекцию!):
a0. Выделяем возможные решения исходного уравнения f1(x,y)dx+f2(x,y)dy=0. Первое: f1(x,y0)=0. Это дает одно из решений: y=y0=–2– прямая, параллельная оси ОХ. Второе: f2(x0,y)=0 не добавляет решений: при фиксированном x=x0 переменная y остается произвольной.
a1. Учитывая, что теперь f2(x,y) ≠ 0, перепишем заданное ДУ: y′= 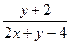 .
.
a2. Применим преобразование: x=u+m; y=v+n, что определяет параллельный перенос системы координат XOY.
a3. Выбираем числа: m, n из системы: 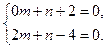 Имеем: m=3, n=–2. Запишем обратное преобразование: u=x–3; v=y+2 для использования при записи окончательного выражения ответа.
Имеем: m=3, n=–2. Запишем обратное преобразование: u=x–3; v=y+2 для использования при записи окончательного выражения ответа.
a4. Запишем преобразованное уравнение: v′= 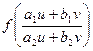 =
= 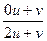 =
= 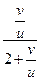 – однородное уравнение.
– однородное уравнение.
a5. Примем 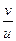 =z; получим выражение: φ(z)=f(z)–z=–
=z; получим выражение: φ(z)=f(z)–z=– 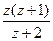 .
.
a6. Проверим условие: φ(z0)= f(z0)– z0=0. Получаем два решения. Первое из них: прямая: z=0, или v=0, или y+2=0, то есть прямая параллельная оси ОХ. Второе решение: z+1=0, или z=–1, или v=– u, или y+x=1.
a7. Учитывая, что теперь f(z)–z≠0, запишем ДУ в виде: – 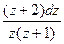 =
= 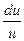 . (1)
. (1)
a8. Находим интеграл: J=– 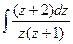 =
= 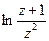 .
.
a9. Записываем результат интегрирования уравнения (1): 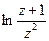 =lnCu. Записываем общее решение ДУ, учитывая что z=
=lnCu. Записываем общее решение ДУ, учитывая что z= 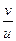 : → С(y+2)2=x+y–1.
: → С(y+2)2=x+y–1.
Ответ: С(y+2)2=x+y–1 – общее решение ДУ, также y+2=0 и y+x=1 (выделяется из общего при значении С=0).
Пример 6–60: Решить дифференциальное уравнение: (x+y+1)dx–(2x+2y–1)dy =0.
Решение:
1). Заданное ДУ – специального вида: множители при dx и dy – линейные функции, их отношение образует специальную дробь: 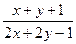 . Так как прямые l1: x+y+1=0 и l2:2x+2y–1=0 параллельны: их нормальные векторы
. Так как прямые l1: x+y+1=0 и l2:2x+2y–1=0 параллельны: их нормальные векторы 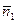 =(1,1) и
=(1,1) и 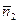 =(2,2) коллинеарны, то имеем Случай-2 уравнения специального вида. Далее используется «стандартный алгоритм» для этого случая.
=(2,2) коллинеарны, то имеем Случай-2 уравнения специального вида. Далее используется «стандартный алгоритм» для этого случая.
2). Данное уравнение решаем, применяя алгоритм «Случай-2» (см. Лекцию!):
a0. Выделяем возможные решения исходного уравнения f1(x,y)dx+f2(x,y)dy=0. Условия: f1(x,y0)=0 и f2(x0,y)=0 не дают решений: если фиксировать одну переменную, вторая остается произвольной. Это значит, что указанные условия невыполнимы.
a1. Учитывая, что теперь f2(x,y) ≠ 0, перепишем заданное ДУ: y′= 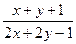 . (1)
. (1)
a2. Применим преобразование: u=x+y. Отсюда: y′=u′–1.
a3. Перепишем уравнение (1): u′= 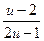 . Заметим, что u=2 есть решение уравнения, то есть x+y =2 – одно из решений заданного ДУ.
. Заметим, что u=2 есть решение уравнения, то есть x+y =2 – одно из решений заданного ДУ.
a4. Разделим переменные в последнем уравнении: 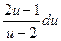 = dx. (2)
= dx. (2)
a5. Находим интеграл: J= 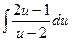 =2u+3ln|u–2|. Тогда решение (2): 2u+3ln|u–2|=x+С.
=2u+3ln|u–2|. Тогда решение (2): 2u+3ln|u–2|=x+С.
a6. Учитывая u=x+y, записываем общее решение ДУ: x+2y+3ln|x+y–2|=С.
Ответ: x+2y+3ln|x+y–2|=С – общее решение ДУ, также x+y =2 (из общего не выделяется).
Пример 7–62: Решить дифференциальное уравнение: y′–tg 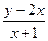 =
= 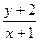 .
.
Решение:
1). Заданное ДУ только слегка намекает на уравнение специального вида. Преобразуем дробь, которая является аргументом тангенса: 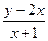 =
= 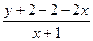 =
= 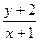 –2. Теперь видим уравнение вида: y′=φ
–2. Теперь видим уравнение вида: y′=φ 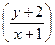 , то есть специального вида. Так как прямые l1: y+2=0 и l2: x+1=0 перпендикулярны: их нормальные векторы
, то есть специального вида. Так как прямые l1: y+2=0 и l2: x+1=0 перпендикулярны: их нормальные векторы 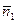 =(0,1),
=(0,1), 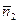 =(1,0) и скалярное произведение векторов:
=(1,0) и скалярное произведение векторов: 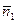 ∙
∙ 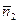 =0, то имеем Случай-1 уравнения специального вида. Далее используется «стандартный алгоритм» для этого случая.
=0, то имеем Случай-1 уравнения специального вида. Далее используется «стандартный алгоритм» для этого случая.
2). Данное уравнение решаем, применяя алгоритм «Случай-1» (см. Лекцию!):
a0. Выделяем возможные решения исходного уравнения y′= f(x,y). Нет таких: при фиксированном y=y 0 переменная x остается произвольной.
a1. Применим преобразование: x=u+m; y=v+n, что определяет параллельный перенос системы координат XOY.
a2. Выбираем числа: m, n из системы: 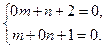 Имеем: m=–1, n=–2. Запишем обратное преобразование: u=x+1; v=y+2 для использования при записи окончательного выражения ответа.
Имеем: m=–1, n=–2. Запишем обратное преобразование: u=x+1; v=y+2 для использования при записи окончательного выражения ответа.
a3. Запишем преобразованное уравнение: v′= 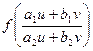 =tg
=tg 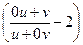 +
+ 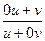 , или v′= tg
, или v′= tg 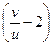 +
+ 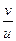 – однородное уравнение.
– однородное уравнение.
a4. Примем 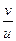 =z; получим выражение: φ(z)=f(z)–z=tg(z–2)+z–z= tg(z–2).
=z; получим выражение: φ(z)=f(z)–z=tg(z–2)+z–z= tg(z–2).
a6. Проверим условие: φ(z0)= f(z0)– z0=0. Получаем решения ДУ: z–2=πn, n 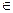 Z, то есть z=2+πn, или v=u(2+πn), или y+2=(x+1)(2+πn), или y=x(2+πn)+πn – семейство прямых. При n=0 получаем выражение: y=2x – прямая, проходящая через начало координат. Замечание: подстановка y=2x в исходное ДУ подтверждает решение!
Z, то есть z=2+πn, или v=u(2+πn), или y+2=(x+1)(2+πn), или y=x(2+πn)+πn – семейство прямых. При n=0 получаем выражение: y=2x – прямая, проходящая через начало координат. Замечание: подстановка y=2x в исходное ДУ подтверждает решение!
a7. Учитывая, что теперь f(z)–z≠0, запишем ДУ в виде: 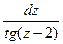 =
= 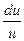 . (1)
. (1)
a8. Находим интеграл: J= 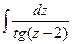 =ln|sin(z–2)|.
=ln|sin(z–2)|.
a9. Записываем результат интегрирования уравнения (1): ln|sin(z–2)|=lnCu, или с учетом z: sin 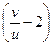 =Cu. Учитывая: u=x+1; v=y+2, записываем общее решение заданного ДУ: sin
=Cu. Учитывая: u=x+1; v=y+2, записываем общее решение заданного ДУ: sin 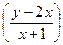 =C(x+1).
=C(x+1).
Ответ: sin 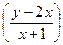 =C(x+1) – общее решение ДУ, также y=x(2+πn)+πn, n
=C(x+1) – общее решение ДУ, также y=x(2+πn)+πn, n  Z.
Z.
Пример 8–177: Найти уравнение кривой, проходящей через точку (3,1), если длина отрезка, отсекаемого любой её касательной на оси ординат, равна поднормали.
В Примере 1–18 получены выражения: отрезка А=OА=(0,y–y′х), – отсекаемого касательной на оси ординат, ND =D–N=(x,0) – (х+yy′,0) =(–yy′,0) – поднормаль.
Решение:
1). Учитывая, что точка А может располагаться с точкой М по одну сторону от оси ОХ и по разные, запишем два варианта использования исходных данных:
▪ [отрезок ОА]= [отрезок ND] → y–y′х=yy′; (1)
▪ [отрезок ОА]= – [отрезок ND] → y–y′х=–yy′. (2)
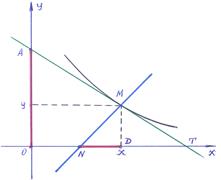 Случай-1.
Случай-1.
2). Решим уравнение (1), записанное в виде: х′= 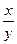 +1:
+1:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0: решение y0=0 геометрически тривиально!
a2. Примем 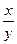 =u; получим: f(u)–u=u+1–u=1.
=u; получим: f(u)–u=u+1–u=1.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Решений дополнительных нет.
a4. Учитывая, что f(u)–u≠0, запишем ДУ (1) в виде: du = 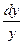 . (3)
. (3)
a5. Интегрируем уравнение (3): u= C+ lny.
a6. Записываем общее решение ДУ. Учитывая что u= 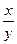 , получаем: x= y(C+ lny), или y=С
, получаем: x= y(C+ lny), или y=С 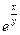 – общее решение уравнения (1).
– общее решение уравнения (1).
Случай-2.
3). Решим уравнение (2), записанное в виде: х′= 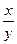 –1:
–1:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0: решение y0=0 геометрически тривиально!
a2. Примем 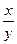 =u; получим: f(u)–u=u–1–u=–1.
=u; получим: f(u)–u=u–1–u=–1.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Решений дополнительных нет.
a4. Учитывая, что f(u)–u≠0, запишем ДУ в виде (1): –du = 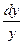 . (4)
. (4)
a5. Интегрируем уравнение (3): –u= lny+C, или (удобнее!): u =C– lny.
a6. Записываем общее решение ДУ. Учитывая что u= 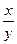 , получаем: x= y(C– lny).
, получаем: x= y(C– lny).
4). Объединим результаты решения уравнений (1) и (2): x= y(C ± lny).
5). Выделим частное решение (интегральную кривую, проходящую через точку (3,1)):
3=1(C ± ln1) → C=3 → частное решение: x= y(3± lny).
Ответ: x= y(C ± lny) – общее решение ДУ; частное решение: x= y(3± lny).
Замечание: Нетрудно заметить совпадение результатов решения задачи в Примере 8–00 для Случая-2 и Случая-1 рассматриваемой задачи. По общим заданным свойствам семейства представленных кривых существенно отличаются, но решения совпадают!
* * * * * * * * * *
Домашнее задание
| Дома | Л-3 | гл.10: № 46, 51, 54, 61, 64, 173. |
Пример 1–46: Решить дифференциальное уравнение: y′ =  +
+ 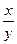 .
.
Решение:
1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
2). Данное уравнение решаем, применяя общий алгоритм «А» (см. Лекцию!):
3). В нашем случае:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0. Их нет.
a2. Примем  = u; получим: φ(u)=f(u)–u= u+
= u; получим: φ(u)=f(u)–u= u+ 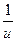 –u=
–u= 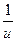 .
.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Решений дополнительных нет.
a4. Учитывая, что f(u)–u≠0, запишем ДУ в виде (1): 2udu =2 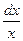 .
.
a5. Интегрируем уравнение (1): u2= lnCx2.
a6. Записываем общее решение ДУ. Учитывая что u=  , получаем: y2= x2lnCx2.
, получаем: y2= x2lnCx2.
Ответ: y2= x2lnCx2 – общее решение ДУ.
Пример 2–51: Решить дифференциальное уравнение: y2dx+ x2dy = xydy.
Решение:
1). Заданное ДУ – однородное: множители при dx и dy – однородные функции 2-го порядка (одинакового!). Далее используется «стандартный алгоритм» решения уравнения, заданного в дифференциальной форм: y2dx+(x2–xy)dy=0.
2). Данное уравнение решаем, применяя общий алгоритм «В» (см. Лекцию!):
a0. Выделяем возможные решения исходного уравнения f1(x,y)dx+f2(x,y)dy=0.Имеем: f1(x,y)=y2; f2(x,y) =x2–xy. Первое: f1(x,y0)=0 при каких y0=0– ось ОХ. Второе условие: f2(x0,y)=0. Даёт решение: x=x0=0– ось ОY.
a1. Запишем наше уравнение в виде: y′= 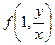 : y′=–
: y′=– 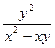 =
= 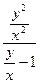 . Здесь учтено: f2(x,y)=x≠ 0.
. Здесь учтено: f2(x,y)=x≠ 0.
a2. Примем  = u; получим выражение: φ(u)=f(u)–u=
= u; получим выражение: φ(u)=f(u)–u= 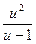 –u=
–u= 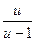 .
.
a3. Проверим условие: φ(u0)=0: имеем u0=0 → y=0: уже участвует согласно a0.
a4. Учитывая, что теперь f(u)–u≠0, записываем уравнение: 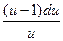 =
= 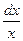 . (1)
. (1)
a5. Находим интеграл: J= 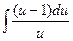 =u–ln|u|.
=u–ln|u|.
a6. Записываем результат интегрирования уравнения (1): u–ln|u|=lnCx → u=ln(Cux). Записываем общее решение ДУ. Учитывая что u =  , получаем:
, получаем: 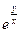 =Cy.
=Cy.
Ответ: 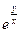 =Cy – общее решение ДУ, также x=0, y=0 (из общего не выделяются ни при каком С).
=Cy – общее решение ДУ, также x=0, y=0 (из общего не выделяются ни при каком С).
Пример 3–54: Решить дифференциальное уравнение: xy′ =y+ xtg  .
.
Решение:
0). Представим ДУ в виде: y′ =  + tg
+ tg  . Деление на x≠0.
. Деление на x≠0.
1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
2). Данное уравнение решаем, применяя общий алгоритм «А» (см. Лекцию!):
3). В нашем случае:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0. Видим: y0=0 –решение ДУ.
a2. Примем  = u; получим: φ(u)=f(u)–u=u+tgu–u=tgu.
= u; получим: φ(u)=f(u)–u=u+tgu–u=tgu.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Следует: u0=πn, n 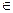 Z, которые являются решениями ДУ, то есть y=x∙πn, n
Z, которые являются решениями ДУ, то есть y=x∙πn, n 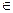 Z – семейство прямых, проходящих через начало координат XOY. При n=0 получаем найденное ранее y0 =0 – ось ОХ.
Z – семейство прямых, проходящих через начало координат XOY. При n=0 получаем найденное ранее y0 =0 – ось ОХ.
a4. Учитывая, что теперь f(u)–u≠0, запишем ДУ в виде (1): 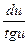 =
= 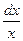 .
.
a5. Интегрируем уравнение (1): ln|sinu|= lnCx.
a6. Записываем общее решение: sinu=Cx. Учитывая что u=  , получаем: sin
, получаем: sin  =Cx.
=Cx.
Ответ: sin  =Cx – общее решение ДУ, также y=x∙πn, n
=Cx – общее решение ДУ, также y=x∙πn, n  Z.
Z.
Пример 4–61: Решить дифференциальное уравнение: (x+y–1)2dy=2(y+2)2dx.
Решение:
1). Заданное ДУ – специального вида: множители при dx и dy – линейные функции, их отношение образует специальную дробь: 2 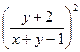 . Так как прямые l1: 0x+y+2=0 и l2: x+y–1=0 пересекаются: их нормальные векторы
. Так как прямые l1: 0x+y+2=0 и l2: x+y–1=0 пересекаются: их нормальные векторы 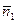 =(0,1) и
=(0,1) и 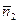 =(1,1) не коллинеарны, то имеем Случай-1 уравнения специального вида. Далее используется «стандартный алгоритм» для этого случая.
=(1,1) не коллинеарны, то имеем Случай-1 уравнения специального вида. Далее используется «стандартный алгоритм» для этого случая.
2). Данное уравнение решаем, применяя алгоритм «Случай-1» (см. Лекцию!):
a0. Выделяем возможные решения исходного уравнения f1(x,y)dx+f2(x,y)dy=0. Первое: f1(x,y0)=0. Это дает одно из решений: y=y0=–2– прямая, параллельная оси ОХ. Второе: f2(x0,y)=0 не добавляет решений: при фиксированном x=x0 переменная y остается произвольной.
a1. Учитывая, что теперь f2(x,y) ≠ 0, перепишем заданное ДУ: y′=2 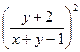 .
.
a2. Применим преобразование: x=u+m; y=v+n, что определяет параллельный перенос системы координат XOY.
a3. Выбираем числа: m, n из системы: 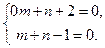 Имеем: m=3, n=–2. Запишем обратное преобразование: u=x–3; v=y+2 для использования при записи окончательного выражения ответа.
Имеем: m=3, n=–2. Запишем обратное преобразование: u=x–3; v=y+2 для использования при записи окончательного выражения ответа.
a4. Запишем преобразованное уравнение: v′= 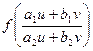 =2
=2 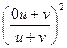 =2
=2 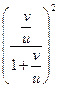 – однородное уравнение.
– однородное уравнение.
a5. Примем 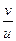 =z; получим выражение: φ(z)=f(z)–z=–
=z; получим выражение: φ(z)=f(z)–z=– 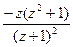 .
.
a6. Проверим условие: φ(z0)= f(z0)– z0=0. Получаем решение: z=0, или v=0, или y+2=0, то есть прямая параллельная оси ОХ.
a7. Учитывая, что теперь f(z)–z≠0, запишем ДУ в виде: – 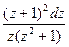 =
= 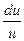 . (1)
. (1)
a8. Находим интеграл: J=– 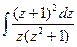 =–
=– 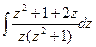 =–ln|z|–2arctgz.
=–ln|z|–2arctgz.
a9. Записываем результат интегрирования уравнения (1): –ln|z|–2arctgz=lnCu, или в более удобной форме: –2arctgz=lnCuz Записываем общее решение ДУ, учитывая что z= 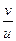 и u=x–3; v=y+2 запишем: → –2arctg
и u=x–3; v=y+2 запишем: → –2arctg 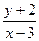 =lnC(y+2).
=lnC(y+2).
Ответ: –2arctg 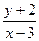 =lnC(y+2) – общее решение ДУ, также y+2=0 (из общего не выделяется ни при каком значении С).
=lnC(y+2) – общее решение ДУ, также y+2=0 (из общего не выделяется ни при каком значении С).
Пример 5–64: Решить дифференциальное уравнение: xy′=yln  , y(1)=1.
, y(1)=1.
Решение:
0). Представим ДУ в виде: y′ =  ln
ln  . Деление на x≠0.
. Деление на x≠0.
1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
2). Данное уравнение решаем, применяя общий алгоритм «А» (см. Лекцию!):
3). В нашем случае:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0. Их нет.
a2. Примем  = u; получим: φ(u)=f(u)–u=ulnu–u.
= u; получим: φ(u)=f(u)–u=ulnu–u.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Следует: невозможно!.
a4. Учитывая, что теперь f(u)–u≠0, запишем ДУ в виде (1): 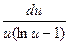 =
= 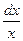 .
.
a5. Интегрируем уравнение (1): ln|lnu–1|= lnCx, или lnu–1=Cx.
a6. Записываем общее решение. Учитывая что u=  , получаем: ln
, получаем: ln  =Cx+1.
=Cx+1.
a7. Найдем частное решение: ln 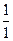 =C1+1 → C=–1 . Частное решение: ln
=C1+1 → C=–1 . Частное решение: ln  =1–x.
=1–x.
Ответ: Общее решение: ln  =Cx+1; частное решение: ln
=Cx+1; частное решение: ln  =1–x.
=1–x.
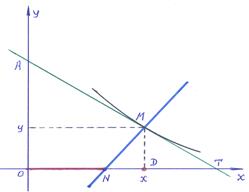
Пример 6–173: Найти уравнение кривой, проходящей через точку (1,0), если длина отрезка оси абсцисс, отсекаемая её нормалью на 2 больше абсциссы точки касания.
В Примере 1–18 получены выражения: N=(х+yy′,0); – отсекаемого касательной на оси абсцисс, D =(х,0) – ординаты.
 Решение:
Решение:
Замечание: Условие задачи предполагает равенство величин: |ON|= (x+2).
Через некоторую точку М(x,y) плоскости OXY проходит кривая y=(y) с заданными свойствами, которые могут быть определены вариантами:
▪ [отрезок ОN]= [отрезок ОD+2] → х+yy′= х+2; (1)
▪ [отрезок ОN]=–[отрезок ОD+2]→ х+yy′=–(х+2).. (2)
Случай-1.
1). Запишем уравнение (1), в виде: yy′=2:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0: их нет!
a2. Интегрируем уравнение (1): y2=4x+C– общее решение уравнения (1): семейство парабол
a3. Определим частное решение для точки А(1,0): C= –4, получаем: y2=4(x–1).
Случай-2.
2). Решим уравнение (2), записанное в виде: yy′=–2(х+1):
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0: их нет!
a2. Интегрируем уравнение (1): y2= –2(х+1)2+C– общее решение уравнения (2): семейство концентрических окружностей с центром в точке (–1,0).
a3. Определим частное решение для точки А(1,0): C= 8, получаем: 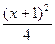 +
+ 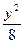 =1.
=1.
Ответ: Случай-1: y2=4(x–1). – частное решение; Случай-2: 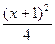 +
+ 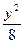 =1 частное решение.
=1 частное решение.
☻
Вопросы для самопроверки:
1. Какое уравнение называют дифференциальным?
2. Что такое решение ДУ, частное решение ДУ?
3. Что такое общее решение ДУ?
4. Что значит решить Задачу Коши?
5. Каковы стандартные формы однородных ДУ?
6. Какова стандартная схема решения однородных ДУ?
7. Какова стандартная форма уравнений, приводящихся к однородным ДУ?
< * * * * * >
