Тест №2. «Уравнения и неравенства»
МАТЕМАТИКА
Профильный ЕГЭ проводится для выпускников и абитуриентов, планирующих использовать математику и смежные дисциплины в будущей профессиональной деятельности. Результаты профильного ЕГЭ по математике переводятся в стобалльную шкалу и могут быть представлены абитуриентом на конкурс для поступления в вуз.
СТРУКТУРА ЭКЗАМЕНАЦИОННОЙ РАБОТЫ
Профильный уровень
Минимальный порог – 27 баллов.
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий.
Определяющим признаком каждой части работы является форма заданий:
· часть 1 содержит 9 заданий (задания 1–9) с кратким ответом;
· часть 2 содержит пять заданий (задания 10–14) с кратким ответом и семь заданий (задания 15 - 21) с развёрнутым ответом.
КАК ПОДГОТОВИТЬСЯ К ЕГЭ ПО МАТЕМАТИКЕ
Задания к ЕГЭ по математике – контрольные измерительные материалы (КИМ) – разработаны специалистами ФИПИ на основе школьной программы. Поэтому к экзамену можно готовиться по школьным учебникам, рекомендованным и допущенным Минобрнауки России, консультируясь при необходимости со своим учителем.
Вам нужно определиться с оценкой, которую вы рассчитываете получить на ЕГЭ. Проконсультируетесь по этому поводу со своим учителем или обратитесь за «экспертизой» к другому специалисту. Однако и ваше собственное представление о своих возможностях играет не последнюю роль. Когда вы определитесь с оценкой, вы сможете соответствующим образом планировать свои занятия. Желаем успехов!
Для успешной подготовки к сдаче профильной математики и для поступления в ВолГАУ на факультет биотехнологий и ветеринарной медицины преподавателями ВолГАУ подготовлены тесты, включающие основные темы и разделы.
Одним из важных моментов успешной подготовки к ЕГЭ является самоподготовка.
Предлагается всего 6 тестов: 5 из них составлены в соответствии с распределением заданий экзаменационной работы по содержательным блокам курса; последний 6-й обобщенный тест; кроме того рассматривается демонстрационный вариант, состоящий из 2-х частей с ответами для 1-й части и с ответами и решениями - для 2-й.
| Тест | Тема теста | Кол-во баллов | Сроки сдачи |
| Алгебра | октябрь'15 | ||
| Уравнения и неравенства | ноябрь'15 | ||
| Функции | январь'16 | ||
| Начала математического анализа | февраль'16 | ||
| Тригонометрия и геометрия | март'16 | ||
| Обобщенный тест | май'16 | ||
| Итого |
Тесты выполняются самостоятельно и сдаются в по электронной почте для проверки.
Демонстрационный вариант
Часть 1.
1) Билет на автобус стоит 15 рублей. Какое максимальное число билетов можно будет купить на 100 рублей после повышения цены билета на 20%?
Ответ: 5.
2) На графике показано изменение температуры воздуха на протяжении трех суток. На оси абсцисс отмечается время суток в часах, на оси ординат – значение температуры в градусах. Определите по графику наибольшую температуру воздуха 15 августа. 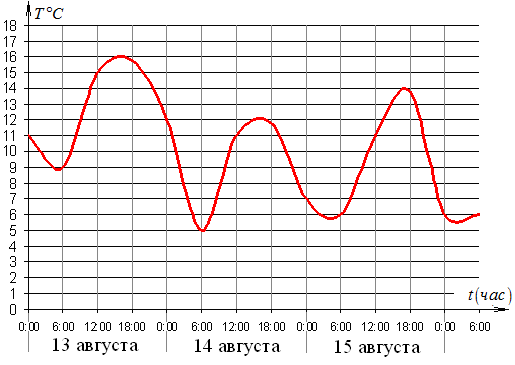
Ответ: 14.
3) Найдите корень уравнения 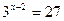
Ответ: 5.
4) В треугольнике АВС угол С равен 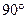 , АВ=5, cosA=0,8. Найдите BC.
, АВ=5, cosA=0,8. Найдите BC. 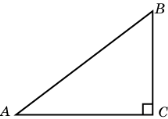
Ответ: 3
5) Строительная фирма планирует купить 70 м  пеноблоков у одного из трех поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей нужно заплатить за самую дешевую покупку с доставкой?
пеноблоков у одного из трех поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей нужно заплатить за самую дешевую покупку с доставкой?
| Поставщик | Стоимость пеноблоков (руб. за 1 м 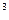 ) ) | Стоимость доставки (руб.) | Дополнительные условия доставки |
| При заказе товара на сумму свыше 150000 рублей доставка бес- платная. | |||
| При заказе товара на сумму свыше 200000 рублей доставка бес- платная. |
Ответ: 192000.
6) Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах.
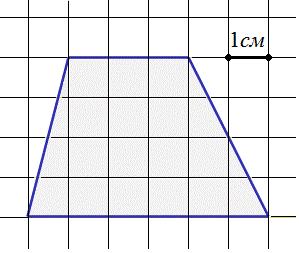
Ответ:18.
7) Найдите значение выражения 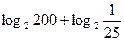
Ответ:3.
8) На рисунке изображен график функции 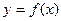 и касательная к этому графику в точке с абсциссой, равной 3. Найдите значение производной этой функции в точке
и касательная к этому графику в точке с абсциссой, равной 3. Найдите значение производной этой функции в точке 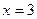 .
.
Ответ: 2.
9) Объем первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания – в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
Ответ: 9.
Часть 2
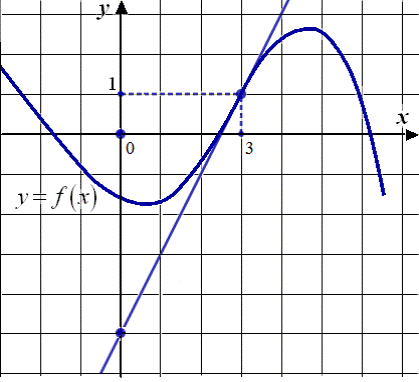
10) Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой 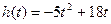 (
( 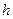 – высота в метрах,
– высота в метрах, 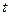 – время в секундах, прошедшее с момента броска). Найдите, сколько секунд камень находился на высоте не менее 9 метров.
– время в секундах, прошедшее с момента броска). Найдите, сколько секунд камень находился на высоте не менее 9 метров.
Ответ: 2,4.
11) Найдите наибольшее значение функции
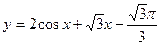 на отрезке
на отрезке 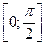
Ответ: 1.
12) Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй – за три дня?
Ответ: 20.
13) Решите систему уравнений
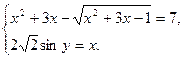
Решение.
1. Сделаем замену 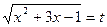 . Тогда
. Тогда 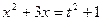 . Теперь первое уравнение системы можно привести к виду:
. Теперь первое уравнение системы можно привести к виду: 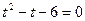 .
.
Корни: 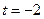 или
или 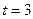 .
.
Получаем: 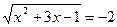 или
или 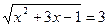 .
.
Первое из этих уравнений не имеет корней. Решим второе:
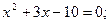
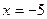 или
или 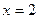 .
.
2. При каждом из найденных значений 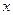 решим второе уравнение системы.
решим второе уравнение системы.
а) Если 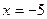 , то
, то 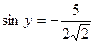 .
.
Поскольку 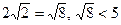 , получаем, что
, получаем, что 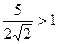 . Значит, уравнение
. Значит, уравнение 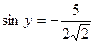 не имеет решений, поскольку его правая часть меньше -1.
не имеет решений, поскольку его правая часть меньше -1.
б) Если 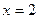 , то
, то 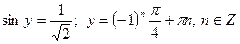 .
.
Ответ: 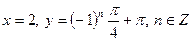 .
.
Возможны другие формы записи ответа. Например:
А) 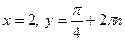 или
или 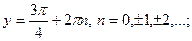
Б) 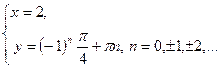
В) 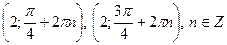
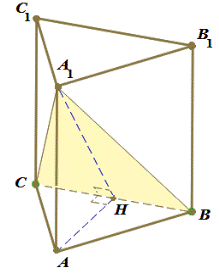
14) Сторона основания правильной треугольной призмы 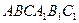 равна 2, а диагональ боковой грани равна
равна 2, а диагональ боковой грани равна 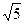 . Найдите угол между плоскостью
. Найдите угол между плоскостью 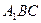 и плоскостью основания призмы.
и плоскостью основания призмы.
Решение:
Обозначим 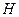 середину ребра
середину ребра 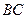 (см. рисунок). Так как треугольник
(см. рисунок). Так как треугольник 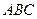 равносторонний, а треугольник
равносторонний, а треугольник 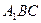 – равнобедренный, отрезки
– равнобедренный, отрезки 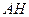 и
и 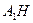 перпендикулярны
перпендикулярны 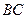 . Следовательно,
. Следовательно, 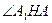 – линейный угол двугранного угла с гранями
– линейный угол двугранного угла с гранями 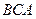 и
и 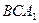 .
.
Из треугольника 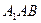 найдем:
найдем: 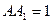 .
.
Из треугольника 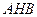 найдем:
найдем: 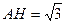 .
.
Из треугольника 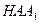 найдем:
найдем: 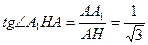 .
.
Искомый угол равен 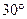 .
.
Ответ: 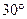 .
.
Возможны другие формы записи ответа. Например:
А) 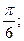
Б) 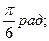
В) 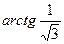 и т.п.
и т.п.
Возможны другие решения.Например, решение задачи с использованием векторов или метода координат.
15) Решите неравенство 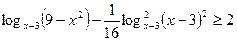 .
.
Решение:
Преобразуем неравенство:
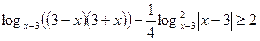 .
.
Найдем, при каких значениях 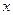 левая часть неравенства имеет смысл:
левая часть неравенства имеет смысл:
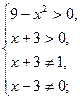
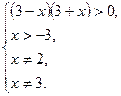

Получаем: 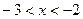 или
или 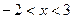 .
.
Значит, 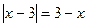 при всех допустимых значениях
при всех допустимых значениях 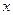 . Поэтому
. Поэтому
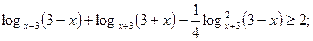
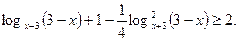
Сделаем замену 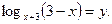 Получаем:
Получаем:
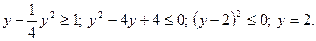
Таким образом, 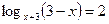 , откуда
, откуда 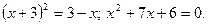
Корни уравнения: -6 и -1. Условию 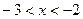 или
или 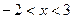 удовлетворяет только один
удовлетворяет только один 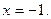
Ответ: -1.
Замечание.Можно не находить область допустимых значений x , а прийти к соотношению 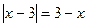 другим способом. Тогда решение будет немного короче.
другим способом. Тогда решение будет немного короче.
Преобразуем неравенство:
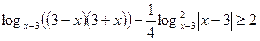
Заметим, что x + 3 > 0 и (3- x)(3+ x) > 0. Значит, 3- x > 0.
Поэтому 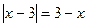 . Получаем:
. Получаем:
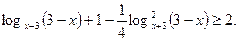
Сделаем замену 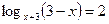 . Получаем:
. Получаем:
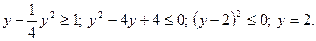
Таким образом,
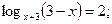
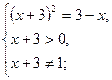
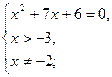
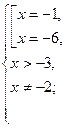
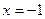 .
.
Ответ: -1.
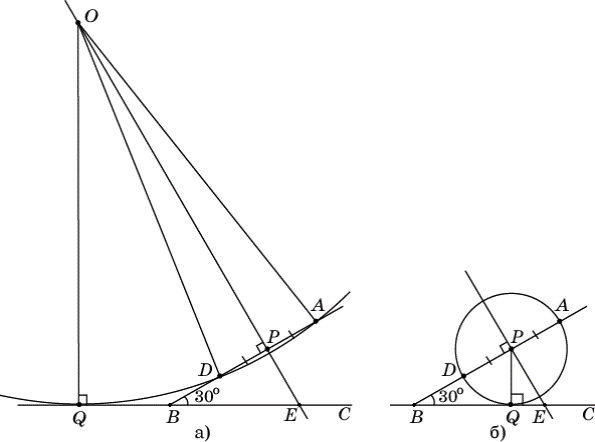
16) На стороне BA угла АВС, равного 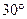 , взята такая точка D, что AD=2 и BD=1. Найдите радиус окружности, проходящей через точки A, D и касающейся прямой BC.
, взята такая точка D, что AD=2 и BD=1. Найдите радиус окружности, проходящей через точки A, D и касающейся прямой BC.
Решение:
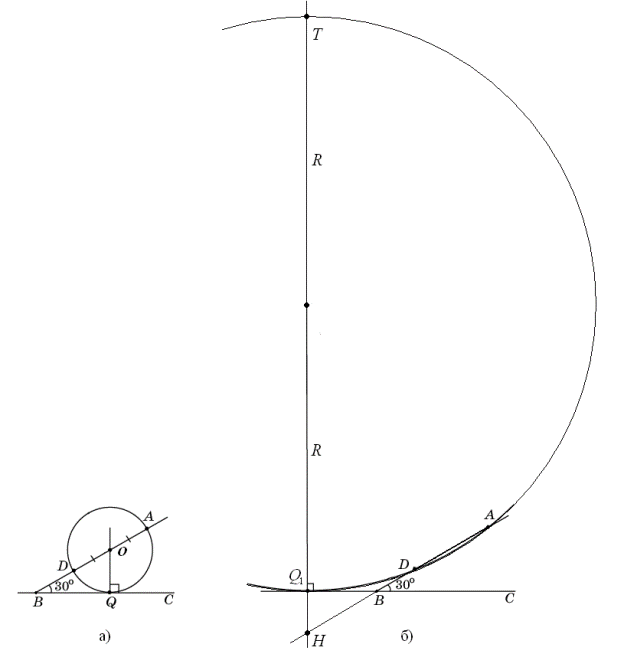
Центр O искомой окружности принадлежит серединному перпендикуляру к отрезку AD. Обозначим P середину отрезка AD, Q – основание перпендикуляра, опущенного из точки O на прямую BC, E – точку пересечения серединного перпендикуляра с прямой BC (см. рисунок а). Из условия касания окружности и прямой BC следует, что отрезки OA, OD и OQ равны радиусу R окружности.
Заметим, что точка O не может лежать по ту же сторону от прямой AB, что и точка E, так как в этом случае расстояние от точки O до прямой BC меньше, чем расстояние от нее до точки A. O
Из прямоугольного треугольника BPE с катетом BP = 2 и 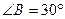 находим, что PE =
находим, что PE = 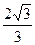 . Так как OA = R и
. Так как OA = R и 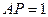 , получаем:
, получаем:
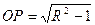 и, следовательно,
и, следовательно, 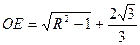 .
.
Из прямоугольного треугольника OQE, в котором 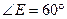 , находим:
, находим:
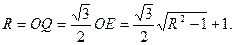
В результате получаем уравнение для R:
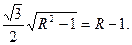
Возведем в квадрат обе части этого уравнения и приведем подобные члены. Получим уравнение 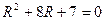 , решая которое находим два корня R1 = 1, R2 = 7. Если радиус равен 1, то центром окружности является точка P(см. рисунок б).
, решая которое находим два корня R1 = 1, R2 = 7. Если радиус равен 1, то центром окружности является точка P(см. рисунок б).
Ответ:1 или 7.
Другое решение.Пусть точка 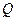 касания окружности с прямой лежит на луче
касания окружности с прямой лежит на луче 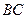 (см. рисунок а). По теореме о касательной и секущей
(см. рисунок а). По теореме о касательной и секущей
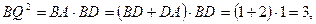
откуда 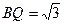 .
.
Пусть 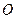 – точка пересечения луча
– точка пересечения луча 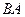 и перпендикуляра к
и перпендикуляра к 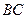 , проведенного через точку
, проведенного через точку 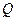 . Из прямоугольного треугольника BQO находим:
. Из прямоугольного треугольника BQO находим:
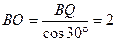 , тогда
, тогда 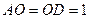 и
и 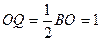 .
.
Таким образом, точка 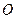 удалена от точек A, D и Q на одно и то же расстояние, равное 1. Следовательно,
удалена от точек A, D и Q на одно и то же расстояние, равное 1. Следовательно, 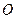 – центр искомой окружности, а ее радиус равен 1.
– центр искомой окружности, а ее радиус равен 1.
Пусть теперь точка 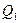 касания окружности с прямой лежит на продолжении
касания окружности с прямой лежит на продолжении 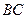 за точку
за точку 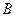 (см. рисунок б), а прямая, проходящая через точку
(см. рисунок б), а прямая, проходящая через точку 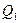 перпендикулярно
перпендикулярно 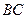 , пересекает прямую
, пересекает прямую 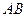 в точке
в точке 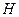 , а окружность вторично – в точке
, а окружность вторично – в точке 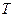 . Тогда 1
. Тогда 1
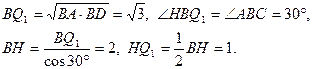
Если 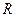 – радиус окружности, то
– радиус окружности, то 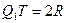 . По теореме о двух секущих ,
. По теореме о двух секущих , 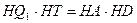 ,то есть
,то есть 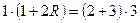 , откуда находим, что
, откуда находим, что 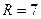 .
.
Ответ:1 или 7.
Возможны другие формы записи ответа. Например,
А) 1, 7;
Б) радиус окружности равен 7 или 1.
17) Найдите все значения a, при каждом из которых уравнение
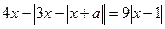
имеет хотя бы один корень.
Решение:
Запишем уравнение в виде 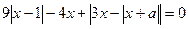 .Функция
.Функция 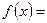
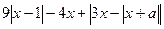 непрерывна и
непрерывна и
1) неограниченно возрастает при 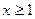 , так как при любом раскрытии модулей имеем
, так как при любом раскрытии модулей имеем
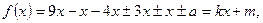
где 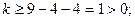
2) убывает при 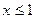 , так как при любом раскрытии модулей имеем
, так как при любом раскрытии модулей имеем
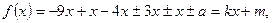
где 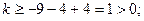
Следовательно, наименьшее значение функция 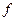 принимает при
принимает при 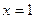 , и уравнение
, и уравнение 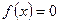 будет иметь корень тогда и только тогда, когда
будет иметь корень тогда и только тогда, когда 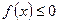 .
.
Решим это неравенство:
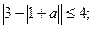
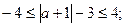
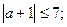
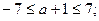
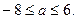
Ответ: 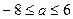 .
.
Возможны другие формы записи ответа. Например:
А) 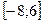 ;
;
Б) 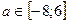 .
.
18) Найдите все такие пары взаимно простых натуральных чисел (то есть чисел, наибольший общий делитель которых равен 1) a и b, что если к десятичной записи числа a приписать справа через запятую десятичную запись числа b, то получится десятичная запись числа, равного 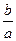 .
.
Решение:
Пусть десятичная запись числа b состоит из n цифр. Тогда по условию задачи можно записать равенство
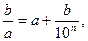 поэтому
поэтому 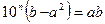 (1)
(1)
Из этого уравнения следует, что 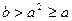 . Так как числа a и b взаимно простые, числа
. Так как числа a и b взаимно простые, числа 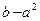 и ab тоже взаимно простые. (Действительно, пусть p – общий простой делитель этих чисел. Тогда если p делитель a , то p будет делителем b . Если же p – делитель b , то p будет делителем
и ab тоже взаимно простые. (Действительно, пусть p – общий простой делитель этих чисел. Тогда если p делитель a , то p будет делителем b . Если же p – делитель b , то p будет делителем 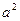 , значит, p – делитель a . Противоречие.)
, значит, p – делитель a . Противоречие.)
Поэтому 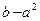 =1 и, следовательно,
=1 и, следовательно, 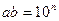 . Последнее равенство при взаимно простых a и b возможно только в двух случаях:
. Последнее равенство при взаимно простых a и b возможно только в двух случаях:
1) 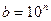 , a =1, но в этом случае не выполняется равенство
, a =1, но в этом случае не выполняется равенство 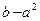 =1.
=1.
2) 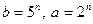 . В этом случае равенство
. В этом случае равенство 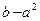 =1 принимает вид
=1 принимает вид
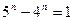 , откуда
, откуда 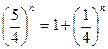 .
.
Функция 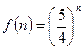 возрастает, а функция
возрастает, а функция 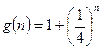 убывает. Поэтому уравнение f (n) = g(n) имеет не более одного корня, и так как f (1) = g(1) , единственным корнем уравнения является n =1.
убывает. Поэтому уравнение f (n) = g(n) имеет не более одного корня, и так как f (1) = g(1) , единственным корнем уравнения является n =1.
Ответ: а=2, b=5.
Возможны другие формы записи ответа.Например:
А) 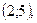
Б) 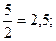
В) 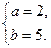
Тест №1. «Алгебра»
Проверяемые требования: умение выполнять вычисления и преобразования, использовать приобретенные знания и умения в практической деятельности и повседневной жизни.
| № | уровень | задание | балл | |
| Б | Найдите длину отрезка 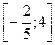 | |||
| Б | Выполните действия: 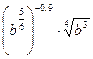 | |||
| Б | Найти наибольшее целое число, не превосходящее числа 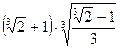 | |||
| Б | Велосипедист собирается проехать из пункта А в пункт Е, в который ведут три маршрута: через В, через С и через D. Расстояния в километрах между соседними пунктами показаны на схеме. Известно, что если ехать через В, то средняя скорость будет равна 16 км/ч, если ехать через D – то 18 км/ч, а если через С – то 20 км/ч. Велосипедист выбрал маршрут так, чтобы доехать до Е за наименьшее время. Сколько часов он будет в пути? 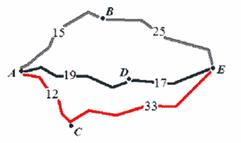 | |||
| Б | На рисунке показано изменение уровня воды водохранилища в течение 12 часов во время паводка. Как только уровень воды превысил отметку 10 метров, через сливные отверстия в плотине начали сбрасывать воду до того момента, пока её уровень понизился до отметки 10 метров. Определите, сколько часов длился сброс воды. 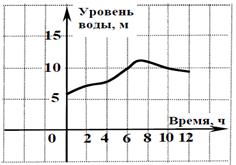 | |||
| Б | Объемы ежегодной добычи нефти первой, второй и третьей скважинами относятся как 6:7:10. Планируется уменьшить годовую добычу нефти из первой скважины на 10% и из второй – тоже на 10%. На сколько процентов нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объем добываемой за год нефти не изменился? | |||
| П | При каком целом положительном х значение выражения 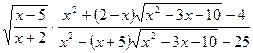 ближе всего к - 0,7? ближе всего к - 0,7? | |||
| max 9 баллов | ||||
Тест №2. «Уравнения и неравенства»
Проверяемые требования: Умение решать уравнения и неравенства, строить и исследовать простейшие математические модели.
(в пунктах 1,2,3 выполнить одно из предлагаемых заданий)
| № | уровень | задание | балл | |
| Б | Решить уравнение 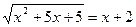 | |||
Решить уравнение 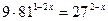 | ||||
Решить уравнение 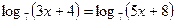 | ||||
| Б | Решить неравенство 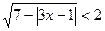 и указать число целых решений. и указать число целых решений. | |||
При каких 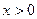 выполняется неравенство выполняется неравенство 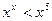 ? В ответе указать число целых решений неравенства. ? В ответе указать число целых решений неравенства. | ||||
Найдите число целых решений неравенства 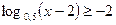 | ||||
| П | Найдите наименьшее натуральное решение неравенства 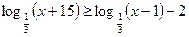 | |||
Решить неравенство 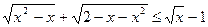 | ||||
Найти сумму корней уравнения 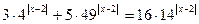 | ||||
| П | Найти наименьшее целое решение неравенства 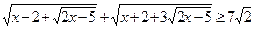 | |||
| П | Найти сумму решений системы 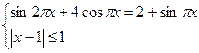 | |||
| В | Выяснить, сколько действительных корней имеет уравнение 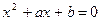 , если известно, что , если известно, что 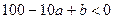 | |||
| max 12 баллов | ||||
Тест №3. «Функции»
Проверяемые требования: Умение выполнять действия с функциями
