Действия над событиями

Над событиями можно производить различные действия, получая при этом другие события. Дадим определения этих действий.

Определение 2.13.

Если при всяком испытании, при ко­тором происходит событие А, происходит и событие В, то событие А называется частным случаем события В.

Говорят также, что А влечет за собой В, и пишут: 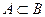(А вложено в В) или 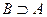(рис. 2.1).

Например, пусть событие А состоит в появлении двух очков при бросании игральной кости, а событие В состоит в появлении четного числа очков при бросании игральной кости В = {2; 4; 6}. Тогда событии А есть частный случай события В, так как два — четное число. Можем записать .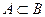

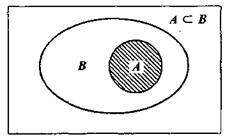
Рис. 2.1. Событие А — частный случай события В

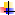Определение 2.14.

Если А влечет за собой В, а В влечет за собой А, то эти события равносильны, так как они вместе наступают или вместе не наступают.

Из того, что 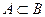и 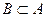( следует) А = В.

Например, А — событие, состоящее в том, что на иг­ральной кости выпала четная цифра меньше трех. Это со­бытие равносильно событию В, состоящему в том, что на игральной кости выпала цифра 2.

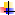Определение 2.15.

Событие, состоящее в совместном на­ступлении обоих событий и А, и В, называется пересече­нием этих событий А∩В, или произведением этих собы­тий АВ (рис. 2.2).

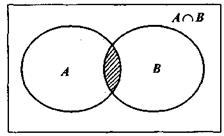
Рис. 2.2.Пересечение событий

Например, пусть событие А состоит в выпадении четно­го числа очков при бросании игральной кости, тогда его наступлению благоприятствуют элементарные события, состоящие в выпадении 2-х, 4-х и 6-ти очков. А - {2; 4; 6}. Событие В состоит в выпадении числа очков больше трех при бросании игральной кости, тогда его наступлению бла­гоприятствуют элементарные события, состоящие в выпа­дении 4-х, 5-ти и 6-ти очков. В = {4; 5; 6}. Тогда пересечени­ем или произведением событий А и В будет событие, состо­ящее в выпадении четного числа очков, большего трёх (выполняется и событие А, и событие В):

А∩В =АВ= {4; 6}.

Пересечением событий, одно из которых А — выпадение дамы из колоды карт, а другое В — выпадение трефы, будет трефовая дама.

Примечание. Если два события А и В несовместны, то их совместное наступление невозможно АВ = 0.

Определение 2.16.

Событие, состоящее в наступлении или события А, или события В (хотя бы одного из событий, по крайней мере одного из этих событий), называется их объединением А и В, или суммой событий А и В и обо­значается через А+В (рис. 2.3).

Рис. 2.3.Объединение событий

Например, событие А состоит в выпадении четного чис­ла очков при бросании игральной кости, тогда его наступ­лению благоприятствуют элементарные события, состоящие в выпадении 2-х, 4-х и 6-ти очков, или А - {2; 4; 6}. Собы­тие В состоит в выпадении числа очков больше трех при бросании игральной кости, тогда его наступлению благо­приятствуют элементарные события, состоящие в выпаде­нии 4-х, 5-ти и 6-ти очков, или В = (4; 5; 6}. Тогда объедине­нием, или суммой событий А и В будет событие, состоящее в выпадении хотя бы одного из них — либо четного числа очков, либо числа очков большего трёх (выполняется или событие А, или событие В):

А ∩ В =А +В= {2; 4; 5; 6}.

Определение 2.17.

Событие, состоящее в том, что собы­тие А не происходит, называется противоположным со­бытию А и обозначается через Ā (рис. 2.4).

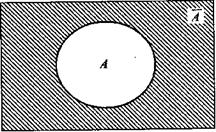
Рис. 2.4.Противоположные события

Например, пусть событие А состоит в выпадении четного числа очков при бросании игральной кости, тогда его на­ступлению благоприятствуют элементарные события, состо­ящие в выпадении 2-х,-4-х и 6-ти очков, или А = {2; 4; 6}. Тогда событие Ā состоит в выпадении нечетного числа оч­ков, и его наступлению благоприятствуют элементарные события, состоящие в выпадении 1-го, 3-х и 5-ти очков. Ā ={1;3;5}.

Определение 2.18.

Событие (А и В) , состоящее в том, что А происходит, а 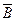не происходит, называется разно­стью событий А и В и обозначается через А-В. Впрочем, можно обойтись без этого обозначения, так как из опре­деления следует, что А - В - 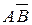(рис. 2.5).

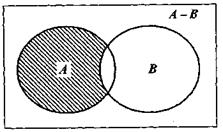
Рис. 2.5.Разность событий А и В

Например, пусть событие А состоит в выпадении чет­ного числа очков при бросании игральной кости, тогда А = {2; 4; 6}. Событие В состоит в выпадении числа очков больше трех. В = {4; 5; 6}.

Тогда 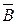— событие, состоящее в выпадении числа очков не больше трех, и его наступлению благоприятствуют эле­ментарные события, состоящие в выпадении 1-го, 2-х и 3-х очков. 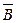= {1; 2; 3}.

Разностью событий А и В будет событие, состоящее в том, что выполняется событие А и не выполняется событие В. Его наступлению благоприятствует элементарное событие, состоящее в выпадении 2-х очков:

А-В= А∩ 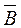= {2}.

Определения суммы и произведения событий распростра­няются и на большее число событий:

А + В + ... + N = (А или В, или ... или N) (2.1)

есть событие, состоящее в наступлении хотя бы одного из событий А, В, ... N;

АВ ... N = (А и В и... и N), (2.2)

есть событие, состоящее в совместном наступлении всех со­бытий А, В, ... N.

Аналогично определяются сумма и произведение беско­нечного числа событий А₁, А₂, ... А_п, ...

Отметим, что все же некоторые правила алгебры сохра­няются и для действий над событиями. Например, имеет место перёместительный закон (коммуникативность):

А + В = В + А, АВ=ВА, (2.3)

выполняется распределительный закон (дистрибутивность):

(А +В) С = АС + ВС, (2.4)

так как левая и правая части представляют событие, состоя­щее в том, что происходят событие С и по крайней мере одно из событий А и В. Справедлив также сочетательный закон (ассоциативность):

А+(В + С) = (А+В)+ С = А+В + С;

А(ВС) = (АВ)С = АВС. (2.5)

Кроме того, имеют место и такие равенства, которые в обычной алгебре показались бы нелепыми. Например, для любых А, В, С:

АА=А (2.6)

А+А = А (2.7)

А+АВ = А (2.8)

АВ + С = (А+С)(В+С) (2.9)

Противоположные события связаны:

· законом двойного отрицания:

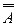= А; (2.10)

· законом исключенного третьего

А + 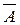= Ω. (сумма их есть достоверное событие); (2.11)

· законом противоречия:

А 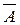= Ø(произведение их невозможное событие). (2.12)

Равенства (2.6)-(2.12) доказываются для высказываний в курсе дискретной математики. Предлагаем читателю про­верить это самостоятельно, используя определения суммы и произведения событий.

Если В = А₁ + А₂+... +А_п и события А попарно несовме­стимы, т.е. каждое несовместимо с остальными: А_jА_k = Ø при i≠k говорят, что событие В подразделяется на част­ные случаи А₁, А ₂, ..., А_п. Например, событие В, состоящее в выпадении нечетного числа очков, подразделяется на част­ные случаи Е₁, Е₃, Е₅, состоящие соответственно в выпаде­нии 1, 3 и 5 очков.

Исходя из определения действий над событиями, мы мо­жем дать более четкое определение полной группе событий.

Определение 2.19.

Если А₁ + А₂+... +А_п = Ω, т.е. если хотя бы одно из событий А₁ + А₂+... +А_п непременно дол­жно осуществиться и если при этом А_j попарно несовме­стимы (т.е. достоверное событие Ω подразделяется на частные случаи А₁ + А₂+... +А_п), то говорят, что события А₁ + А₂+... +А_п образуют полную группу событий. Таким образом, если А₁ + А₂+... +А_п — полная группа событий, то при каждом испытании обязательно происходит одно и только одно из событий А₁ + А₂+... +А_п.

Например, при бросании игральной кости полную груп­пу событий составляют также события Е₁, Е₂, Е₃, Е₄, Е₅ и Е₆, состоящие соответственно в выпадении 1, 2, 3,4, 5 и 6 очков.