Независимость событий
План лекции
1. Алгебра и s-алгебра событий
2. Аксиоматическое определение вероятности. Свойства вероятности.
3. Условная вероятность. Независимость событий.
4. Формулы полной вероятности. Формула Байеса.
Наша цель – определить вероятность таким образом, чтобы рассмотренные ранее подходы были бы частным случаем этого определения. Для этого придется ввести некоторые ограничения на то, какие подмножества множества пространства элементарных исходов 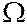 мы будем считать событиями.
мы будем считать событиями.
Пусть пространство элементарных исходов есть некоторое множество 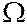 , а F – некоторая система подмножеств данного множества.
, а F – некоторая система подмножеств данного множества.
F называется алгеброй, если
А1. 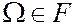
А2. Из того, что 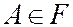 и
и 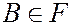 следует что
следует что 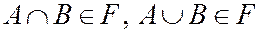 .
.
А3. Если 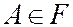 , то
, то 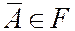 .
.
В условии А2 достаточно требовать выполнение только одного из двух условий. Действительно, если 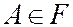 ,
, 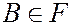 , то
, то 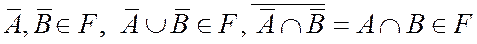 .
.
( 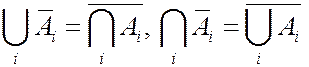 - формулы де Моргана)
- формулы де Моргана)
F называется s-алгеброй, если свойство А2 выполняется для любых последовательностей множеств;
А2’. Если 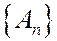 есть последовательность множеств из F , то
есть последовательность множеств из F , то
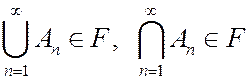 .
.
Таким образом, алгебра есть класс множеств, замкнутый относительно конечного числа операций объединения, пересечения, дополнения, а s-алгебра - класс множеств, замкнутый относительно счетного числа этих операций.
Если задано множество 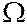 и какая-нибудь s-алгебра его подмножеств, то говорят, что задано измеримое пространство
и какая-нибудь s-алгебра его подмножеств, то говорят, что задано измеримое пространство 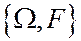 .
.
Для того, чтобы формализовать некоторую вероятностную задачу, надо соответствующему эксперименту приписать измеримое пространство 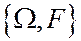 . При этом
. При этом 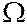 означает пространство элементарных исходов эксперимента, а s-алгебра выделяет класс событий. Все подмножества
означает пространство элементарных исходов эксперимента, а s-алгебра выделяет класс событий. Все подмножества 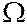 , не входящие в F, событиями не являются.
, не входящие в F, событиями не являются.
Вероятность есть числовая функция, определенная на s-алгебре событий и удовлетворяющая свойствам (аксиомам):
Р1. 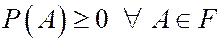
Р2. 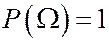
Р3. Если последовательность событий 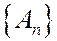 такова, что
такова, что 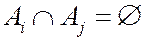 при
при 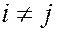 , то
, то
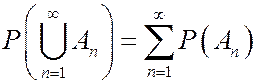 .
.
Аксиома Р3 эквивалентна требованию конечной аддитивности и следующей аксиоме непрерывности.
Р3’. Пусть последовательность событий 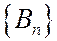 такова, что
такова, что 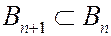
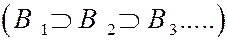 и
и 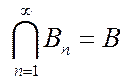 , тогда
, тогда 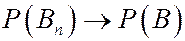 при
при 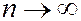 .
.
Доказательство эквивалентности.
1. Предположим выполненным условие счетной аддитивности Р3.
Рассмотрим убывающую последовательность событий 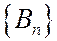 ,
, 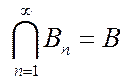 . Тогда последовательность событий,
. Тогда последовательность событий, 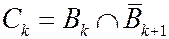 , k=1,2,... состоит из попарно несовместных событий и
, k=1,2,... состоит из попарно несовместных событий и  .
.
Согласно условию счетной аддитивности получим 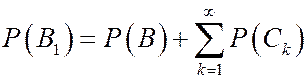 . Соответственно ряд
. Соответственно ряд 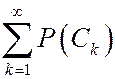 - сходится. Это означает, что остаточные суммы стремятся к нулю, то есть
- сходится. Это означает, что остаточные суммы стремятся к нулю, то есть 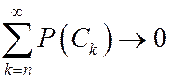 при
при 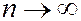 . Поэтому,
. Поэтому, 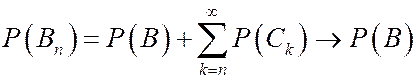 при
при 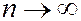 . Таким образом, из условия счетной аддитивности Р3 следует условие непрерывности Р3’.
. Таким образом, из условия счетной аддитивности Р3 следует условие непрерывности Р3’.
2. Предположим выполненным условие непрерывности Р3’ и конечной аддитивности.
Рассмотрим последовательность несовместных событий 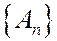 .
.
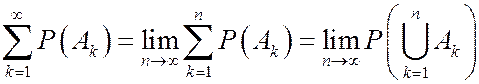
Поскольку 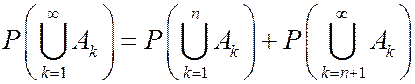 , то
, то 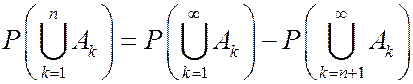 .
.
Поэтому
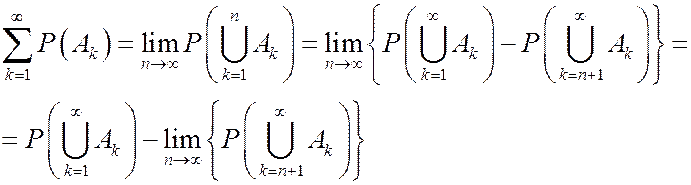 Введем убывающую последовательность событий
Введем убывающую последовательность событий 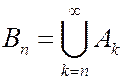 ,
, 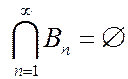 .
.
Согласно Р3’ 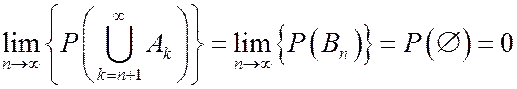 .
.
Поэтому
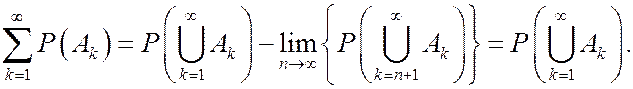
Тройка 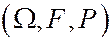 называется вероятностным пространством.
называется вероятностным пространством.
Таким образом, задание вероятностного пространства есть задание счетно-аддитивной меры на измеримом пространстве, такой, что мера 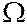 равна 1.
равна 1.
Свойства вероятности.
1. 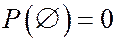
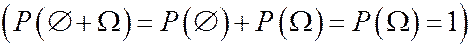
2. 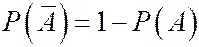
3. Если 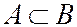 , то
, то 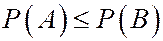 . Это следует из того, что
. Это следует из того, что 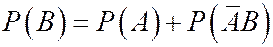 .
.
4. 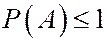 .
.
5. 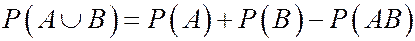
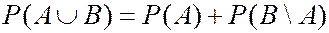 ,
, 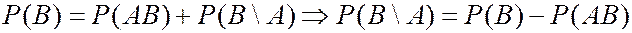 .
.
6. 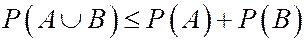
7. 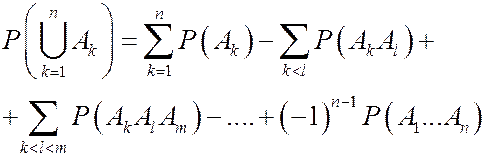
В указанной формуле каждая сумма, содержащая пересечения m событий, имеет 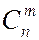 слагаемых. Данная формула доказывается по индукции. При n=2 формула уже доказана. Предположим, что формула верна для объединения любых n-1 событий, так что
слагаемых. Данная формула доказывается по индукции. При n=2 формула уже доказана. Предположим, что формула верна для объединения любых n-1 событий, так что
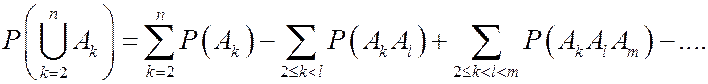
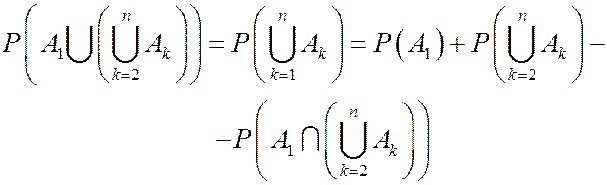 (*)
(*)
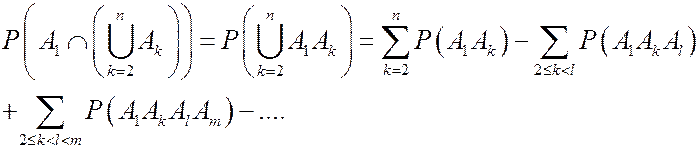 (**)
(**)
Подставим (**) в (*) и получим
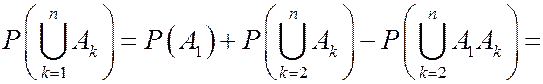
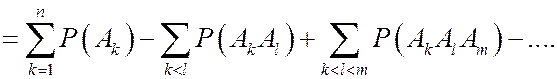
8. Пусть 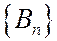 - возрастающая последовательность событий
- возрастающая последовательность событий 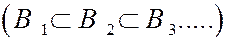 и
и 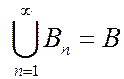 , тогда
, тогда 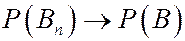 при
при 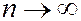 .
.
Действительно, 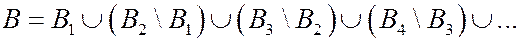 и
и
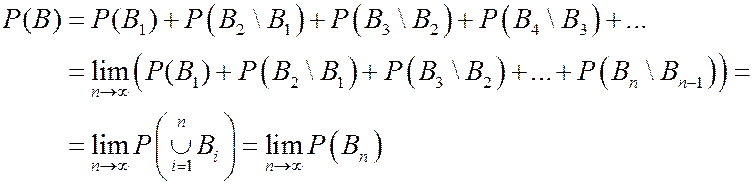
Пример 1. (задача о совпадениях)
Группа студентов имеет одинаковые плащи, которые оказались на одной вешалке. Каждый студент выбирает себе плащ наугад, не имея возможности отличить его от других. Какова вероятность, что хотя бы один плащ попадет к своему владельцу?
Решение.
Пронумеруем плащи 1,…,n. Пронумеруем и студентов, так что k-ый плащ принадлежит k-ому студенту. Каждый элементарный исход разбора плащей можно описать перестановкой 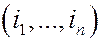 , где ik –номер плаща, взятый k-ым студентом. Обозначим Аk – событие, что k-ый студент взял свой (k-ый) плащ. Событие А –«хотя бы один плащ попадет к своему владельцу», есть объединение событий А1,…, Аn:
, где ik –номер плаща, взятый k-ым студентом. Обозначим Аk – событие, что k-ый студент взял свой (k-ый) плащ. Событие А –«хотя бы один плащ попадет к своему владельцу», есть объединение событий А1,…, Аn: 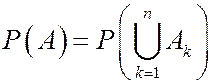 .
.
Подсчитаем вероятность пересечения событий 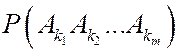 .Данное событие наступает, когда
.Данное событие наступает, когда 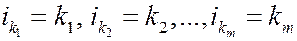 ,а остальные номера могут быть расположены в любом порядке, поэтому
,а остальные номера могут быть расположены в любом порядке, поэтому 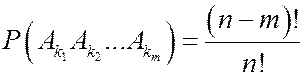 .Различных событий
.Различных событий 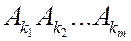 всего насчитывается
всего насчитывается 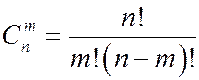 , поэтому
, поэтому 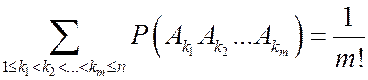 .
.
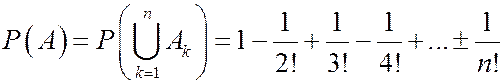 .
.
Искомая вероятность совпадает с частичной суммой ряда 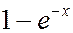 при x=-1, поэтому, при больших n
при x=-1, поэтому, при больших n 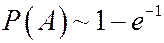 .
.
Пример 2: r шаров случайно размещаются по n ящикам.
Найти вероятность того, что 1) по крайней мере один ящик будет пуст, 2) m ящиков будут пусты.
Решение.
1) Если число шаров r меньше, чем число ящиков n, то пустые ящики будут присутствовать при любом разложении. Поэтому, будем считать, что r>=n. Обозначим Аk – событие, что k-ый ящик пуст. Событие А –«по крайней мере один ящик будет пуст», есть объединение событий А1,…, Аn: 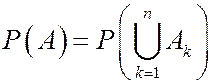 .
.
Подсчитаем вероятность пересечения событий 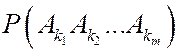 .Данное событие наступает, когда r шаров случайно размещаются по n-m ящикам, поэтому
.Данное событие наступает, когда r шаров случайно размещаются по n-m ящикам, поэтому 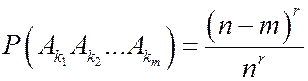 .Различных событий
.Различных событий 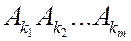 всего насчитывается
всего насчитывается 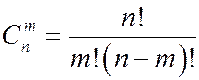 , поэтому
, поэтому 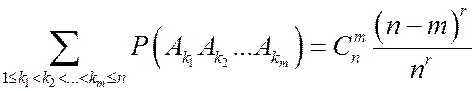 и
и 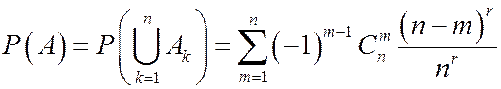 .
.
2)Обозначим 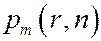 - вероятность того, что m ящиков будут пусты.
- вероятность того, что m ящиков будут пусты.
Вероятность того, что все ящики будут заняты имеет вид 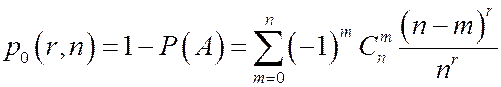 .
.
Рассмотрим размещение, при котором m ящиков оказались пустыми. Эти m ящиков могут быть выбраны 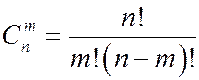 способами, а r шаров случайно размещаются по n-m ящикам, так что каждый из ящиков занят.
способами, а r шаров случайно размещаются по n-m ящикам, так что каждый из ящиков занят.
Число таких распределений равно 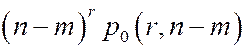 . Множитель
. Множитель 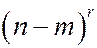 присутствует в последнем выражении, поскольку он присутствует в знаменателе вероятности:
присутствует в последнем выражении, поскольку он присутствует в знаменателе вероятности:
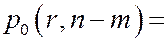 (число способов размещения r шаров по n-m ящ. без пустых ящиков) /
(число способов размещения r шаров по n-m ящ. без пустых ящиков) / 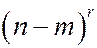 .
.
Таким образом,
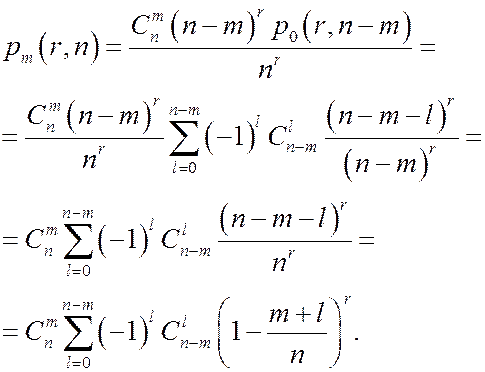
Независимость событий.
Введем несколько новых понятий, характеризующих взаимосвязь событий.
Определение 1. События А и В называются независимыми, если Р(АВ)=Р(А) Р(В).
Определение 2. События А1,…, Аn называются попарно независимыми, если любые два из них независимы..
Определение 3. События А1,…, Аn называются независимыми в совокупности, если для любой группы индексов 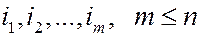
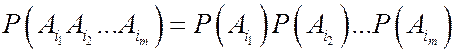 .
.
Из независимости в совокупности следует попарная независимость, обратное – неверно.
Рассмотрим пример. Подбрасываются две монеты. Событие А – на первой монете выпал герб, событие В – на 2-ой монете выпал герб, событие С – выпал один герб.
Легко видеть, что Р(А)= Р(В)= Р(С)=1/2 .
Р(АВ)= Р(АС)= Р(ВС)=1/4, и следовательно события А,В,С попарно независимы. При этом Р(АВС)=0, таким образом события А,В,С не являются независимыми в совокупности.
Условная вероятность.
Начнем с примера. Пусть эксперимент состоит в троекратном подбрасывании монеты. Вероятность того, что герб выпадет 1 раз – событие А= (грр, ргр, ррг) равна 3/8. Предположим, что об исходе эксперимента дополнительно известно, что произошло событие В – «число выпавших гербов нечетно», В=(грр, ргр, ррг, ггг). Какова вероятность события А при наличии этой дополнительной информации? В рамках классической схемы естественно принять новую вероятность события А равной 3/4. Событие В при этом рассматриваем как новое пространство элементарных исходов.
Вероятность события А при условии, что произошло событие В, имеет вид
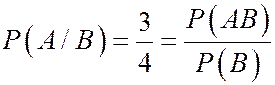 .
.
Рассмотрим более общий пример. Пусть задана классическая схема с n исходами. Событие А состоит из r исходов, событие В – из m исходов, а событие АВ – из k исходов. Вероятность события А при условии, что произошло событие В, естественно определить в виде
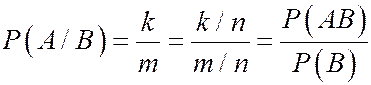 .
.
Определение: Пусть задано ВП 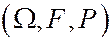 и пусть А и В – произвольные события.
и пусть А и В – произвольные события.
Если Р(В)>0, то условная вероятность события А, при условии, что произошло событие В, по определению полагается равной
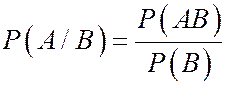 .
.
Определение условной вероятности является согласованным с определением независимости событий. Для независимых событий А и В Р(А/В)=Р(А).
