Элементы комбинаторики

При непосредственном вычислении вероятности события А часто рассматриваются различные комбинации из множества n элементов по m элементов .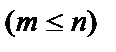

Перестановками из n элементов называются всевозможные упорядоченные множества, содержащие все данные n элементов. Число всех перестановок обозначают 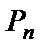и находят по формуле

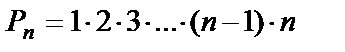или 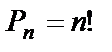(n факториал).

По определению принимают .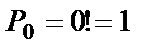

Пример 12. Какие трёхзначные числа можно образовать из неповторяющихся цифр 1, 2, 3.

Решение. 123, 132, 213, 231, 312, 321. Эти числа называются перестановками и их шесть.

Пример 13. Сколько существует способов, чтобы расположить в один ряд на полке 6 книг?

Решение. Число перестановок равно .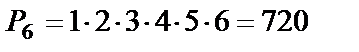

Размещениями из n элементов по m элементов (m<n) называются всевозможные упорядоченные множества по m элементов, образованные из данных n элементов и отличающиеся друг от друга или самими элементами, или их порядком. Обозначается число размещений из n элементов по m элементов символом 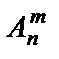и вычисляется по формуле .

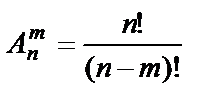Пример 14. Какие двузначные числа можно образовать из цифр 1, 2, 3, если каждая цифра входит в число только один раз?

Решение. 12, 21, 13, 31, 23, 32. Таких цифр шесть.

Пример 15. Студенты данного курса изучают 7 учебных предметов. В расписание занятий можно поставить 3 различных предмета в день. Сколько существует способов, чтобы составить расписание на один день?

Решение. Количество способов равно числу размещений из 7 элементов по 3 элемента: .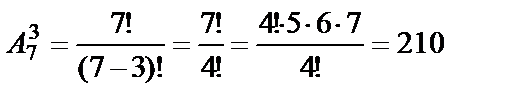

Сочетаниями из n элементов по m элементов называются всевозможные множества по m элементов, образованные из данных n элементов и отличающиеся друг от друга хотя бы одним элементом.

Обозначается число сочетаний из n элементов по m элементов символом .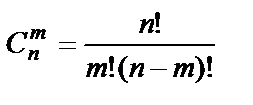

Пример 16. В урне находятся 3 белых шара и 7 чёрных. Из урны наугад извлекают два шара. Сколько существует способов, чтобы извлечь: а) два белых шара; б) два чёрных шара; в) один белый шар и один чёрный?

Решение. а) Так как в урне белых шаров только 3, то количество способов извлечь 2 белых шара равно числу сочетаний из 3 элементов по 2 элемента: .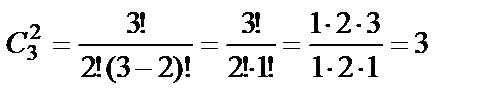

б) Чёрных шаров в урне 7, поэтому количество способов извлечь 2 чёрных шара равно .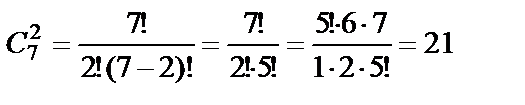

в) Количество способов извлечь один белый шар и один чёрный равно .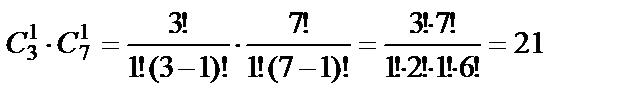

Пример 17. В ящике находятся 20 деталей первого сорта и 10 деталей второго сорта. Из ящика наугад берут 5 деталей. Найти вероятность того, что среди них окажутся 3 детали первого сорта и 2 - второго.

Решение. Обозначим событие A={взятыми окажутся 3 детали первого сорта и 2 - второго}. Искомая вероятность равна 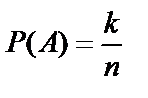, где k – количество способов взять 3 детали первого сорта и 2 – второго, n – количество способов взять 5 деталей из 30. Тогда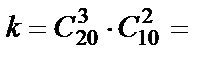

;

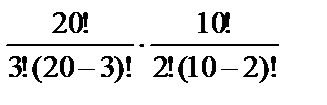
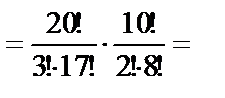
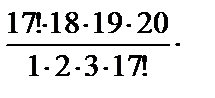
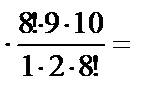
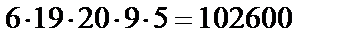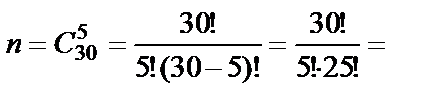
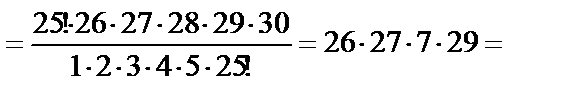134386; .

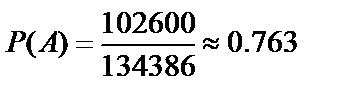Вопросы для самоконтроля знаний

1. Что называется испытанием и событием?

2. Какое событие называется достоверным?

3. Какое событие называется невозможным?

4. Какое событие называется случайным?

5. Какие события называются совместными и несовместными?

6. Какие события называются единственно возможными?

7. Какие события называются противоположными?

8. Какое событие называется благоприятствующим для некоторого другого события?

9. Как формулируется классическое определение вероятности?

10. Чему равны вероятности достоверного, невозможного и случайного событий?

11. Что называется перестановкой, размещением и сочетанием?

12. Как записываются формулы для определения числа перестановок, размещений и сочетаний?