Лабораторная работа № 2

Метод наименьших квадратов

В случае аппроксимации полиномами

Цель работы: научиться аппроксимировать таблично заданные функции методом наименьших квадратов, произвести подгонку экспоненциальной кривой: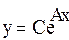

Постановка задачи:

1. Изучить теореточеские сведения.

2. Написать подпрограммы построения аппроксимирующей функции для таблично заданной функции.

3. Определить невязки аппроксимации.

4. Проверить вычисления с помощью встроенных функций.

5. Построить графики аппроксимирующих функций и заданной функции.

Теоретические сведения

Предположим, что заданы точки 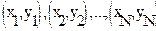и требуется произвести подгонку экспоненциальной кривой:

(1)

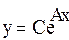
Для процедуры нелинейного метода наименьших квадратов требуется найти минимум:

(2)

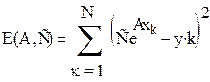
Частные производные Е(А,С) по А и С равны

(3)

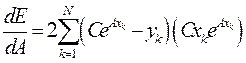
и

(4)

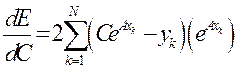
Если положить частные производные в эти формулы равными нулю и затем упростить эти выражения, то можно получить нормальные уравнения

(5)

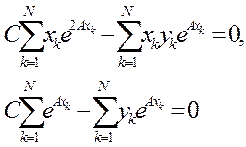
Полученные уравнения- это нелинейные уравнения с неизвестными Аи С, которые можно решить методом Ньютона. На это потребуется только время на вычисления и итерации, для которой нужны хорошие начальные значения для А и С. Во многих пакетах прикладных программ содержатся встроенные подпрограммы и минимизации функций от нескольких переменных, которые можно непосредственно использовать для минимизации функции Е(А,С). Например, симплекс-алгоритм Недлера-Мида можно непосредственно использовать для минимизации и обойтись без данных уравнений.

Пример:Используем МНК и найдем экспоненциальную подгонку y=Ce^Ax по пяти точкам: (0;1,5), (1;2,5), (2;3,5), (3;5,0) и (4;7,5). Для этого минимизируем величину Е(А,С):

Е(А,С)=(C-1,5)² +(Се^А-2,5)²+(Се^2А-3,5)²+(Се^3А-5,0)²+(Се^4А-7,5)²

Воспользуемся командой MATLAB fmins , чтобы найти приближения величин А и С, которые минимизируют Е(А,С) как М-файл в MATLAB.

function z=E(u)

A=u(1);

C=u(2);

z=(C-1,5).^2+(C.*exp(A)-2.5).^2+(C.*exp(2*A)-3.5).^2+… (C.*exp(3*A)-5.0).^2+(C.*exp(4*A)-7.5).^2;

Используя команду MATLAB Сommand Window fmins и начальные значения А=1,0 и С=1,0, найдем

>> fmins(‘E’,[1 1])

ans =

0.38357046980073 1.61089952247928

Такая экспоненциальная подгонка по пяти точкам имеет вид

у=1,6108995е^0,3835705 (подгонка нелинейным МНК).

Степенная прогонка

В некоторых случаях функция имеет вид f(x)=Ax^M, где М- известная постоянная.

Теорема (степенная прогонка):предположим, что {(x_k,y_k)}^N_k=1- N точек с различными абсциссами. Коэффициент А кривой, построенной методом наименьших квадратов, y=Ax^M, равен

(6)

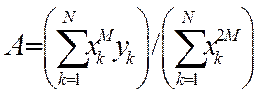
Благодаря технике МНК видим, что минимум функции Е(А) равен

(7)

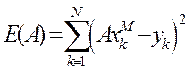
В данном случае достаточно решить уравнение E’(A)=0. Производная равна

(8)

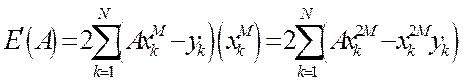
Таким образом, коэффициент А является решением уравнения, которое приводит к равенству, приведенному выше.