Задания для самостоятельного решения. Производная функции
Производная функции
Понятие производной.
Правила дифференцирования. Таблица производных
Пусть 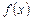 определена в точке
определена в точке 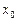 и в некоторой ее окрестности.
и в некоторой ее окрестности.
Пусть 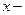 точка рассматриваемой окрестности, то приращением аргумента в точке
точка рассматриваемой окрестности, то приращением аргумента в точке 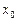 называется величина
называется величина 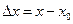 , приращением функции – величина
, приращением функции – величина 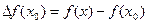 . Если выразить
. Если выразить 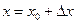 , то
, то 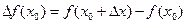 .
.
Производной функции 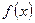 в точке
в точке 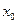 называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, при условии, что предел существует.
называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, при условии, что предел существует.
Производную в точке обозначают 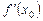 . По определению
. По определению
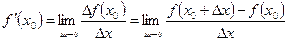 , (1)
, (1)
или, что то же,
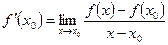 , (2)
, (2)
при условии, что пределы (1),(2) существуют.
Функция, имеющая производную в точке, называется дифференцируемой в этой точке. Операция нахождения производной называется дифференцированием.
Производная функции в точке – это число. Если функция дифференцируема на некотором множестве X из ее области определения, то 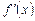 также является функцией (ее обозначают также
также является функцией (ее обозначают также 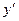 ).
).
Основные правила дифференцирования
Пусть 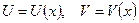 -дифференцируемые функции. Справедливы формулы:
-дифференцируемые функции. Справедливы формулы:
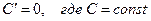 ; (3)
; (3)
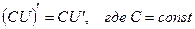 ; (4)
; (4)
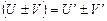 ; (5)
; (5)
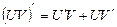 ; (6)
; (6)
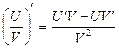 . (7)
. (7)
Таблица производных основных элементарных функций
1)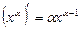 ,где
,где 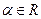 ,
,
в частности
а) 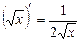 ,
,
б) 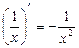 ;
;
2) 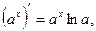 где
где 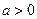 ,
,
в частности
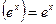 ;
;
3) 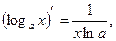 где
где 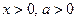 ,
,
в частности
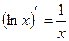 ;
;
4) 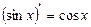 ;
;
5) 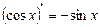 ;
;
6) 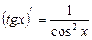 ;
;
7) 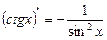 ;
;
8) 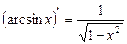 ;
;
9) 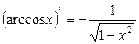 ;
;
10) 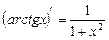 ;
;
11) 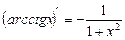 ;
;
12) 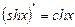 ;
;
13) 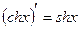 ;
;
14) 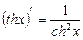 ;
;
15) 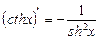 .
.
Пример 1: Найти производную функции 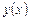 в точке
в точке 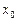 , пользуясь определением, если:
, пользуясь определением, если:
1) 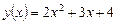 ,
, 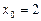 ;
;
2) 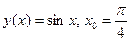 .
.
Решение. 1.Используем определение производной в виде формулы (1):
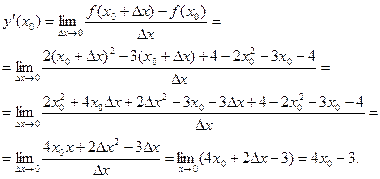
Поскольку по условию 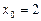 , то
, то 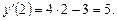
2. По формуле (1) получаем
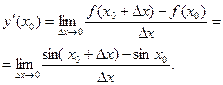
Далее, применив тригонометрическую формулу 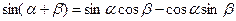 , получим:
, получим:
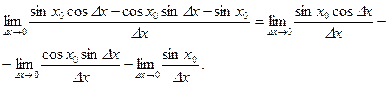
Так как при 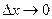 имеем
имеем 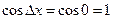 и, применив формулу первого замечательного предела, получаем:
и, применив формулу первого замечательного предела, получаем:
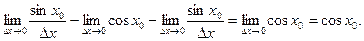
Поскольку по условию 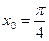 , то
, то 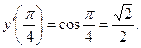
Пример 2:Вычислить производную функции 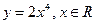 , пользуясь определением производной.
, пользуясь определением производной.
Решение.Пусть 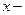 произвольная фиксированная точка из
произвольная фиксированная точка из 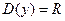 . Пользуясь формулой (1), имеем:
. Пользуясь формулой (1), имеем:
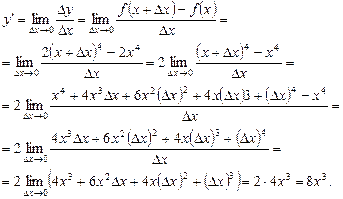
Таким образом, операция дифференцирования ставит в соответствие функции 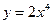 ,
, 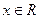 функцию
функцию 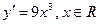 .
.
Пример 3.Найти производную функции:
1) 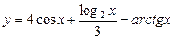 ;
;
2) 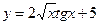 ; 3)
; 3) 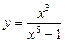 .
.
Решение. 1. Дифференцируем функцию и используем формулы (4), (5) и таблицу производных, получаем:
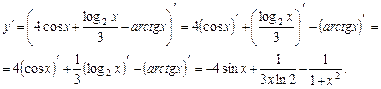
2. Дифференцируем функцию по формулам (3), (4), (6) и соответствующим формулам таблицы производных:
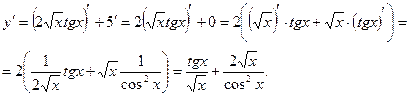
3. Дифференцируем функцию по формулам (7), (5), (3) и первой формуле таблицы производных:
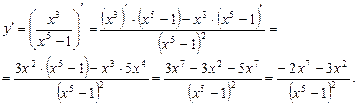
Пример 4. Вычислить производную функции, используя правила дифференцирования и таблицу производных:
1) 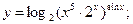 2)
2) 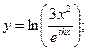 ;
;
3) 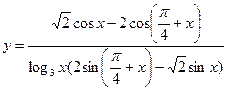
Решение.1. Преобразуем функцию, пользуясь свойствами логарифма:
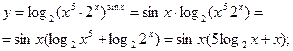
Полученное выражение дифференцируем по формулам (4), (5), (6) и формулам таблицы производных:
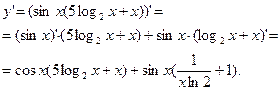
2. Перед дифференцированием преобразуем выражение, пользуясь свойствами логарифма:
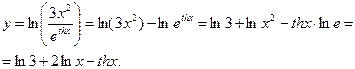
Дальше воспользуемся формулами (3), (4), (5) и таблицей производных:
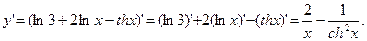
3. Так как непосредственное дифференцирование вызывает значительные трудности, предварительно упростим выражение по формулам тригонометрии:
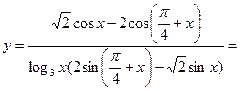
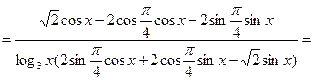
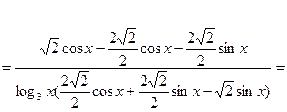
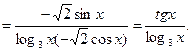
Полученное выражение дифференцируем по формуле (7) и соответствующим формулам таблицы производных.
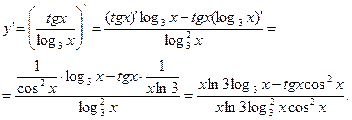
Задания для самостоятельного решения
I уровень
1.1.Пользуясь определением, найдите производную функции:
1) 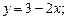 2)
2) 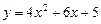
1.2.Найдите производную функции:
1) 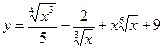 ; 2)
; 2) 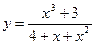 ;
;
3) 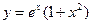 ; 4)
; 4) 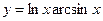 ;
;
5) 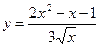 ; 6)
; 6) 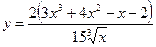 ;
;
7) 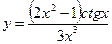 ; 8)
; 8) 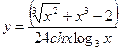 .
.
1.3. Найдите 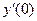 , если
, если
1) 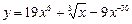 ; 2)
; 2) 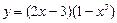 ;
;
3) 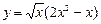 ; 4)
; 4) 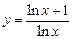 ;
;
5) 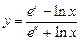 ; 6)
; 6) 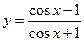 .
.
1.4.Вычислите:
1) 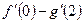 , если:
, если: 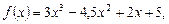
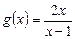 ;
;
2) 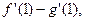 если
если 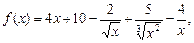
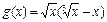 ;
;
3) 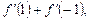 если
если 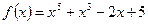 .
.
1.5. Вычислите 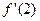 , если
, если 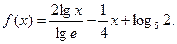
1.6.Вычислите 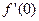 , если
, если 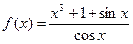 .
.
1.7. Решите уравнение:
1) 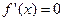 , где
, где 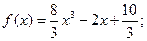
2) 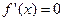 , где
, где 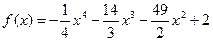 .
.
II уровень
2.1. Найдите производные 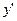 , предварительно преобразовав выражение:
, предварительно преобразовав выражение:
1) 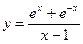 ; 2)
; 2) 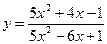 ;
;
3) 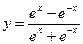 ; 4)
; 4) 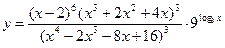 .
.
2.2. Для функции 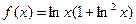 найдите
найдите 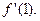
2.3.Известно, что 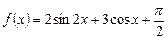 . Найдите
. Найдите 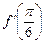 .
.
2.4. Решите неравенство 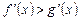 , где
, где 
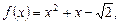
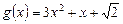 .
.
III уровень
3.1. Вычислите 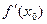 , если:
, если:
1) 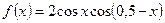 ,
, 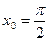
2) 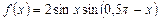 ,
, 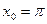 .
.
3.2. Пользуясь определением производной, найдите 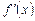 , где
, где
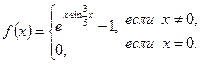
3.3. Найдите значение производной функции 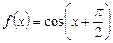 в точке
в точке 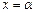 , если
, если 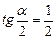 .
.
3.4.Найдите сумму значений производной функции 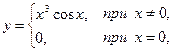 в точках x = 1 и x = 0.
в точках x = 1 и x = 0.
