Матричный метод, метод Крамера

Определение 1.

Системы с n уравнениями и n неизвестными называются системами вида

, (1)

где – коэффициенты системы уравнений, – свободные члены, – неизвестные. В более компактном виде систему (1) можно записать как

. (2)

Системе (1) соответствует основная матрица (А), матрица-столбец переменных (X) и матрица-столбец свободных членов (В) соответственно

, , .

Согласно правилу умножения матриц запишем систему (1) в матричном виде:

. (3)

Определение 2.

Совокупность значений неизвестных , обращающая каждое уравнение системы (1) в числовое равенство, называется решением системы.

Определение 3.

Система называется совместной, если она имеет решения, и несовместной – если решений не имеет.

Определение 4.

Совместная система называется определенной, если имеет одно решение, и неопределенной, если решений множество.

Так как основная матрица квадратная, то существует определитель системы

.

Заменим j-й столбец (при коэффициентах ) столбцом свободных членов. При этом получим j-й определитель :

.

1.1. Метод Крамера

Теорема 1 (Крамера).

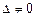Если определитель основной матрицы , то система имеет единственное решение, определяемое по формуле

. (4)

Доказательство.

Умножим каждое уравнение системы на соответствующие алгебраические дополнения к элементам первого столбца, т. е. первое уравнение (1) умножим на , второе уравнение умножим на , треть уравнение умножим на и т. д. Результаты умножения сложим и согласно теореме Лапласа получим:

.

Отсюда следует или . Аналогичным образом, умножая уравнения на алгебраические дополнения последующих столбцов, можно доказать (4) для любого i.

ПРИМЕР 1.

Для системы имеем основную матрицу и определитель

, .

Запишем соответствующие j-е определители для столбцов

, , .

Тогда решение системы: , , . Решение .

1.2. Матричный метод

Если 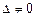системы, то матрица А – невырожденная и существует 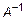. Тогда разрешая систему (3) относительно матрицы неизвестных X, получим уравнение

. (5)

ПРИМЕР 2.

Для системы из предыдущего примера найдем обратную матрицу:

, , , , , , , , . Тогда

,

Результат соответствует методу Крамера.

3. Системы с m линейными уравнениями и n неизвестными

Определение 5.

Системы с m линейными уравнениями и n неизвестными называются системы вида

. (6)

Определение 6.

Расширенной матрицей называется матрица, составленная из основной матрицы путем добавления столбца свободных членов:

.

Теорема 1 (Кронекера – Капелли).

Системы с m линейными уравнениями и n неизвестными совместны тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы .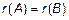

Следствия !!!

1. Если , то система не совместна.

2. Если (числу неизвестных), то система имеет единственное решение. Для отыскания этого решения берут n уравнений и решают любым методом.

33 Если , то система имеет множество решений. В этом случае решения находят следующим образом.

- Пусть .

- За свободные переменные принимают любые 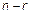неизвестных.

- Оставшиеся r неизвестных выражают через свободные переменные.

- Свободным переменным придают некоторое значение и находят решение известными методами. Для других значений свободных переменных находят другие решения и т. д.

ПРИМЕР 2.

, ,

множество решений. Примем свободных неизвестных. Пусть . Из второго уравнения . Из первого уравнения , или . Запишем решение: .