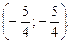Задания для самостоятельного решения. 1.1. Решите уравнение:
I уровень
1.1. Решите уравнение:
1) 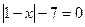 ; 2)
; 2) 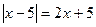 ;
;
3) 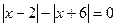 ; 4)
; 4) 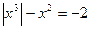 ;
;
5) 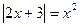 ; 6)
; 6) 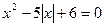 ;
;
7) 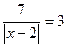 ; 8)
; 8) 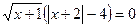 ;
;
9) 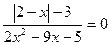 ; 10)
; 10) 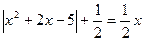 .
.
II уровень
2.1. Решите уравнение:
1) 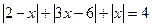 ; 2)
; 2) 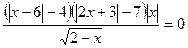 ;
;
3) 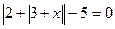 ; 4)
; 4) 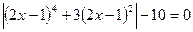 ;
;
6) 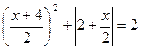 ; 6)
; 6) 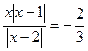 ;
;
7) 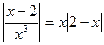 ; 8)
; 8) 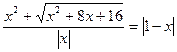 ;
;
9) 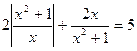 ; 10)
; 10) 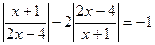 .
.
III уровень
3.1. Решите уравнение:
1) 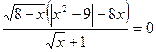 ; 2)
; 2) 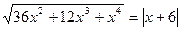 ;
;
3) 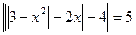 ; 4)
; 4) 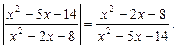
3.2. Решите уравнение:
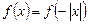 , если
, если 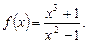
3.3. Найдите все значения а, при которых уравнение 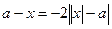 имеет единственный корень.
имеет единственный корень.
3.4. Для каждого а найдите множество решений:
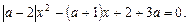
3.5. Определите, при каком значении 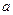 уравнение имеет ровно три решения:
уравнение имеет ровно три решения:
1) 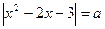 ; 2)
; 2) 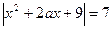 .
.
Системы и совокупности уравнений
Пусть даны два уравнения с двумя неизвестными 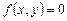 и
и 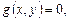 где
где 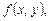
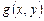 – некоторые выражения с переменными х и у. Если ставится задача найти все общие решения данных уравнений, то говорят, что задана система уравнений:
– некоторые выражения с переменными х и у. Если ставится задача найти все общие решения данных уравнений, то говорят, что задана система уравнений:
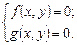 (15)
(15)
Решить систему (15) – значит найти все пары чисел 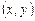 , которые являются решением каждого уравнения, или доказать, что таких пар чисел не существует.
, которые являются решением каждого уравнения, или доказать, что таких пар чисел не существует.
Аналогично определяется понятие системы с тремя и более неизвестными.
Системы, все уравнения которых однородные, называются однородными системами уравнений.
Система называется совместной, если она имеет хотя бы одно решение и несовместной, если таких решений не существует.
Две системы уравнений эквивалентны (равносильны), если они имеют одни и те же решения или обе не имеют решений.
Над уравнениями системы можно выполнять следующие действия, преобразующие данную систему в эквивалентную ей:
1) менять порядок следования уравнений;
2) умножать на число 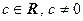 , любое уравнение;
, любое уравнение;
3) умножать на 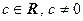 , одно уравнение системы и прибавлять его к другому уравнению.
, одно уравнение системы и прибавлять его к другому уравнению.
Несколько уравнений образуют совокупность уравнений 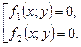 , если ставится задача найти все те решения, которые удовлетворяют хотя бы одному уравнению совокупности и входит в область определения остальных уравнений.
, если ставится задача найти все те решения, которые удовлетворяют хотя бы одному уравнению совокупности и входит в область определения остальных уравнений.
Система двух линейных уравнений с двумя неизвестными имеет вид:
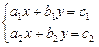 (16)
(16)
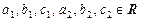 .
.
Геометрически, каждому уравнению системы (16) соответствует прямая линия на плоскости:
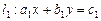 и
и 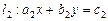
Справедливы утверждения:
1) если 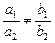 , то система (16) имеет единственное решение (геометрически – прямые
, то система (16) имеет единственное решение (геометрически – прямые 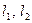 пересекаются в определенной точке);
пересекаются в определенной точке);
2) если 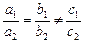 , то система (16) не имеет решений (прямые
, то система (16) не имеет решений (прямые 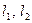 параллельны);
параллельны);
3) если 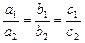 , то система (16) имеет бесконечно много решений (прямые
, то система (16) имеет бесконечно много решений (прямые 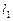 и
и 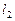 – совпадают).
– совпадают).
Основными методами решения систем уравнений (15) являются:
1) метод подстановки;
2) метод исключения неизвестной;
3) метод сложения;
4) метод умножения (деления) уравнений;
5) метод замены переменных;
6) графический метод.
Пример 1.Решить систему 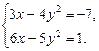
Решение.
Решим методом сложения. Для этого первое уравнение системы умножим на 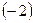 и прибавим ко второму:
и прибавим ко второму:
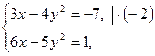 ,откуда следует
,откуда следует 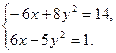
Получаем
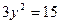 , т.е.
, т.е. 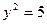 . Значит,
. Значит,
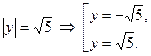
Заданная система сводится к решению совокупности систем:
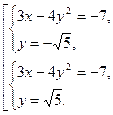
Ее решением являются пары чисел 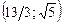 ;
; 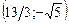 .
.
Пример 2.Решить систему 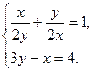
Решение. ОДЗ: 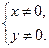
Заменим в первом уравнении системы 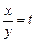 , тогда
, тогда 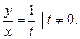
Получим дробно-рациональное уравнение:
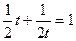 .
.
Решаем его
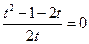 ;
; 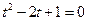 ;
; 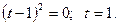
Возвращаемся к переменным х, у:
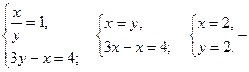 подходит по ОДЗ.
подходит по ОДЗ.
Получили ответ: 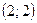 .
.
Пример 3.Решить систему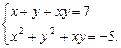
Решение.
Данная система относится к симметрическим системам (неизвестные 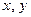 входят одинаково). Решение таких систем производят стандартной заменой переменных
входят одинаково). Решение таких систем производят стандартной заменой переменных 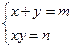 .
.
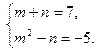 (17)
(17)
Далее используем метод сложения:
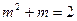 , т.е.
, т.е. 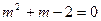 .
.
Получаем корни этого квадратного уравнения:
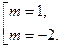
С учетом системы (17) приходим:
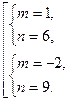
Возвращаясь к переменным х, у, получаем
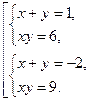
Решим записанные системы отдельно:
1) 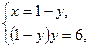 (18)
(18)
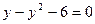 ,
,
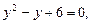
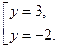
Возвращаясь к системе (18), получаем
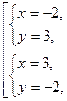
т.е. имеем два решения 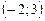 и
и 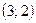 .
.
2) 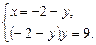 (19)
(19)
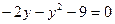 ,
,
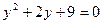 .
.
Поскольку для последнего квадратного уравнения 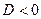 , система (19) не имеет решения.
, система (19) не имеет решения.
Получили ответ: 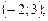
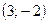 .
.
Пример 4.Решить графически:
1) 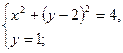 (20)
(20)
2) 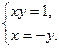
Решение.
1. Исходя из геометрического смысла, 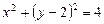 – уравнение окружности с центром
– уравнение окружности с центром 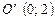 и радиусом
и радиусом 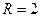 ;
; 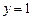 – прямая, параллельная оси
– прямая, параллельная оси 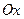 и проходящая через точку
и проходящая через точку 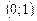
Построим эти линии (рис. 1).
Графики имеют 2 точки пересечения, т.е. система имеет 2 решения, которые найдем из системы (20):
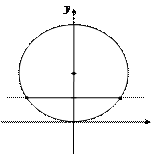 |
Рис.1
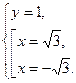
Получили ответ: 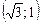 ,
, 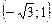 .
.
2. Уравнение 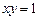 может быть записано в виде
может быть записано в виде 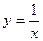 и является уравнением гиперболы .
и является уравнением гиперболы .
Уравнение 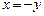 может быть записано в виде
может быть записано в виде 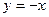 –биссектриса II и IV координатных углов (рис.2).
–биссектриса II и IV координатных углов (рис.2).
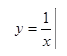 Выполним построение:
Выполним построение:
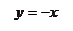

Рис. 2
Графики не имеют точек пересечения и, следовательно, система решений не имеет.
Пример 5.Решить систему 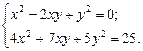
Решение.
Система содержит однородное уравнение.
Так как 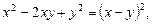 получим:
получим:
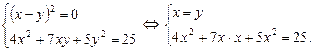
Из второго уравнения найдем х:
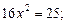
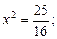
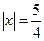 .
.
Получаем совокупность двух систем:
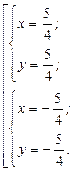
Приходим к ответу: 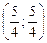 и
и