Определения и свойства групп
ОПРЕДЕЛЕНИЕ 1.1[1] Алгебраической n-местной операцией на множестве  (
( 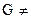 Ø) (или законом композиции) называется правило (закон), по которому каждой упорядоченной
Ø) (или законом композиции) называется правило (закон), по которому каждой упорядоченной 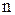 -ке
-ке 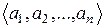 элементов множества
элементов множества  ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 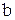 из того же множества
из того же множества  ,
, 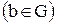 , где
, где 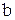 - результат операции.
- результат операции.
Операции в математике обозначаются символами: 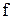 ,
, 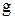 , *, :, ×, +,0,… Если
, *, :, ×, +,0,… Если 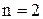 , то операция называется бинарной, при
, то операция называется бинарной, при 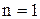 - унарной.
- унарной.
Существует много определений группы. Каждое определение отражает некоторое направление в теории групп. Ближе по духу теории сравнений в группах следующее определение, связанное с решением уравнений, а уравнение (в нашем понимании) – это сравнение относительно отношения равенства.
ОПРЕДЕЛЕНИЕ 1.2 [2] Группой называется непустое множество  с одной основной бинарной алгебраической операцией «×», которая удовлетворяет следующим двум аксиомам:
с одной основной бинарной алгебраической операцией «×», которая удовлетворяет следующим двум аксиомам:
1) 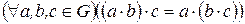 - ассоциативность операции «×»;
- ассоциативность операции «×»;
2) 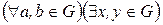 (
( 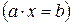 &
& 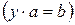 )– уравнения (сравнения)
)– уравнения (сравнения) 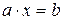 ,
, 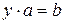 относительно переменных
относительно переменных 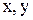 разрешимы в
разрешимы в  , т. е. существуют их решения
, т. е. существуют их решения 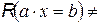 Æ,
Æ, 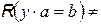 Æ в
Æ в  , где & - знак конъюнкции(«и»).
, где & - знак конъюнкции(«и»).
Эти решения могут оказаться различными. Для операции «×» в общем случае не выполняется закон коммутативности
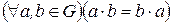 . (1)
. (1)
Если в группе  имеет место формула (1), то группа называется абелевой (в честь норвежского математика Н. Г. Абеля(1802-1829)) или коммутативной.
имеет место формула (1), то группа называется абелевой (в честь норвежского математика Н. Г. Абеля(1802-1829)) или коммутативной.
Будем пользоваться мультипликативной записью операции и соответствующей терминологией. В дальнейшем знак операции «×» опускаем (сохраняя терминологию), что согласуется с принципом экономии и целесообразностью. В тексте мы используем выразительные возможности языка прикладного исчисления предикатов, а также язык теории множеств [1, 2]. Это помогает нам детализировать рассуждения и придавать доказательствам и формулировкам утверждений более компактный и завершенный вид, а это (в свою очередь) позволяет символизировать теорию. Алгебра предикатов (в отличии от алгебры высказываний) за счет анализа субъектно-предикатной структуры высказывательных форм обладает большими выразительными возможностями, что позволяет средствами ее языка полнее отразить закономерности логического мышления, а это способствует более глубокому проникновению в суть вопроса.
Ниже изложены свойства, вытекающие из приведенных выше аксиом группы.
СВОЙСТВО 1. В группе  верна формула
верна формула
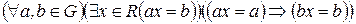 , (2)
, (2)
т. е. элементы группы  обладают правым нейтральным элементом.
обладают правым нейтральным элементом.
ДОКАЗАТЕЛЬСТВО. Рассмотрим произведение 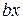 , где
, где 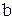 - произвольный элемент группы
- произвольный элемент группы  , а
, а 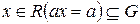 . Существование такого х обеспечено аксиомой 2) (1.1.2). Тогда
. Существование такого х обеспечено аксиомой 2) (1.1.2). Тогда 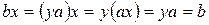 . Отсюда
. Отсюда 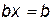 .
.
Свойство доказано.
СВОЙСТВО 2. В группе  верна формула
верна формула
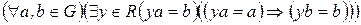 , (3)
, (3)
т. е. элементы группы  обладают левым нейтральным элементом.
обладают левым нейтральным элементом.
ДОКАЗАТЕЛЬСТВО. Рассмотрим произведение 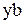 . Так как
. Так как 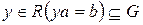 , при b=a, то
, при b=a, то 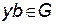 и
и 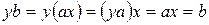 . Таким образом,
. Таким образом, 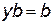 .
.
Свойство доказано.
СВОЙСТВО 3. Группа  обладает единственным нейтральным элементом.
обладает единственным нейтральным элементом.
ДОКАЗАТЕЛЬСТВО. Сначала докажем, что 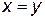 (см. Свойства 1 и 2). Действительно, очевидно
(см. Свойства 1 и 2). Действительно, очевидно 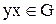 и
и 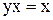 , поскольку
, поскольку 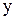 - левый нейтральный элемент группы
- левый нейтральный элемент группы  . С другой стороны
. С другой стороны 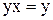 , поскольку
, поскольку 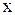 - правый нейтральный элемент группы
- правый нейтральный элемент группы  . Таким образом,
. Таким образом, 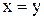 = е и
= е и
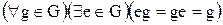 . (4)
. (4)
Далее, установим единственность в группе  нейтрального элемента
нейтрального элемента 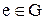 . Предположим, что
. Предположим, что 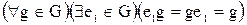 и
и 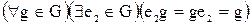 , причем
, причем 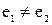 . Из равенств
. Из равенств 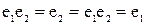 следует, что
следует, что 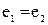 . Противоречие.
. Противоречие.
Свойство доказано.
СВОЙСТВО 4. В группе  каждый элемент обладает единственным обратным (симметричным) элементом.
каждый элемент обладает единственным обратным (симметричным) элементом.
ДОКАЗАТЕЛЬСТВО. Пусть 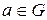 . Очевидно, уравнения
. Очевидно, уравнения 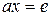 ,
, 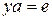 разрешимы в группе
разрешимы в группе  . Пусть
. Пусть 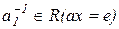 ,
, 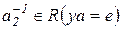 - решения соответствующих уравнений, т. е.
- решения соответствующих уравнений, т. е. 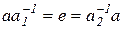 . Докажем, что
. Докажем, что 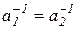 . Предположим, что
. Предположим, что 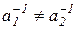 . Рассмотрим элемент
. Рассмотрим элемент 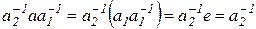 ,
, 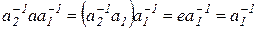 . Отсюда следует, что
. Отсюда следует, что 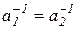 =а-1. Противоречие. Таким образом
=а-1. Противоречие. Таким образом
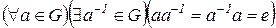 (5)
(5)
Свойство доказано.
СВОЙСТВО 5. В группе  каждое уравнение (сравнение)
каждое уравнение (сравнение) 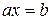 ,
, 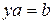 имеет единственное решение.
имеет единственное решение.
ДОКАЗАТЕЛЬСТВО. Очевидно, элемент 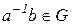 есть решение уравнения
есть решение уравнения 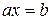 ,так как при подстановке его в уравнение
,так как при подстановке его в уравнение 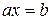 вместо переменной
вместо переменной 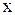 будем иметь
будем иметь 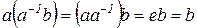 (т. е.
(т. е. 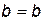 ). С другой стороны, если предположить, что элемент
). С другой стороны, если предположить, что элемент 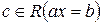 , т. е.
, т. е. 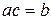 , то
, то 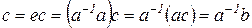 (формула(5)). Таким образом,
(формула(5)). Таким образом, 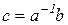 , т. е. других решений уравнения
, т. е. других решений уравнения 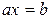 (кроме
(кроме 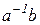 ) в группе
) в группе  нет. Аналогично устанавливается, что элемент
нет. Аналогично устанавливается, что элемент 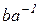 является единственным решением уравнения
является единственным решением уравнения 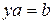 .
.
Свойство доказано.
СВОЙСТВО 6 (Закон сокращения). В группе  верна формула
верна формула
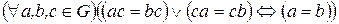 , (6)
, (6)
где « 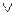 » - знак дизъюнкции(«или»).
» - знак дизъюнкции(«или»).
ДОКАЗАТЕЛЬСТВО. Н е о б х о д и м о с т ь. Пусть 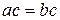 - верное равенство в
- верное равенство в  . Рассмотрим решение
. Рассмотрим решение 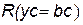 уравнения
уравнения 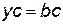 на элементах группы
на элементах группы  относительно переменной
относительно переменной 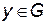 . Очевидно,
. Очевидно, 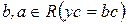 . Так как
. Так как 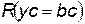 единственно в
единственно в  (Свойство 5), то
(Свойство 5), то 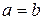 . Если же
. Если же 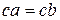 , то рассмотрев уравнение
, то рассмотрев уравнение 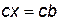 , получим, что
, получим, что 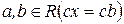 . В силу Свойства 5,
. В силу Свойства 5, 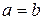 .
.
Д о с т а т о ч н о с ть. Так как 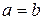 , то из равенства
, то из равенства 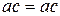 , очевидно, следует равенство
, очевидно, следует равенство 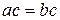 . Аналогично из равенства
. Аналогично из равенства 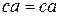 следует, что
следует, что 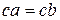 .
.
Свойство доказано.
Таким образом, вышеперечисленные свойства есть свойства коэффициентов указанных уравнений, а вместе с этим характеризуются свойства ассоциативной операции элементов множества G.
Дадим еще одно определение группы, которое, как будет показано, выводится из ранее приведенного.
ОПРЕДЕЛЕНИЕ 1.3[2] Группой называется непустое множество  , на котором определена бинарная алгебраическая операция «×» и унарная алгебраическая операция «
, на котором определена бинарная алгебраическая операция «×» и унарная алгебраическая операция « 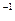 ». Бинарная операция удовлетворяет следующим (аксиомам) условиям:
». Бинарная операция удовлетворяет следующим (аксиомам) условиям:
1) 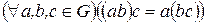 - ассоциативность операции «×»;
- ассоциативность операции «×»;
2) 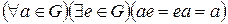 - наличие нейтрального элемента (левого, правого);
- наличие нейтрального элемента (левого, правого);
3) 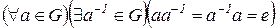 - наличие обратного (симметричного) элемента (левого, правого) элементу
- наличие обратного (симметричного) элемента (левого, правого) элементу 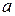 в
в  .
.
Установим равносильность приведенных определений группы. Пусть группа  определена аксиомами 1),2),3) (Определение 1.1.3). Далее, докажем, что уравнения
определена аксиомами 1),2),3) (Определение 1.1.3). Далее, докажем, что уравнения 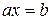 и
и 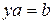 разрешимы в группе
разрешимы в группе 
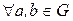 . По аксиоме 3)
. По аксиоме 3) 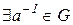 такой, что
такой, что 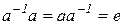 . В группе рассмотрим элементы
. В группе рассмотрим элементы 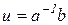 и
и 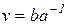 , где
, где 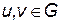 . Очевидно,
. Очевидно, 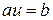 и
и 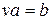 , т.е.
, т.е. 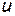 и
и 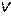 удовлетворяют уравнениям
удовлетворяют уравнениям 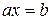 ,
, 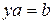 соответственно. Таким образом, уравнения
соответственно. Таким образом, уравнения 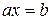 ,
, 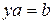 разрешимы в
разрешимы в  . Очевидно, приведенные системы аксиом группы эквивалентны. В зависимости от ситуации, в дальнейшем мы будем пользоваться любой из приведенных систем аксиом и вытекающими из них свойствами. Заметим, что всегда
. Очевидно, приведенные системы аксиом группы эквивалентны. В зависимости от ситуации, в дальнейшем мы будем пользоваться любой из приведенных систем аксиом и вытекающими из них свойствами. Заметим, что всегда
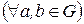
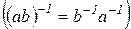 , (7)
, (7)
так как 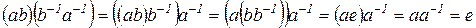 .
.
Аксиома ассоциативности часто используется в формально более сильном виде, чем 1) (см. Определение 1.1.2). Она позволяет опускать скобки и вместо 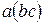 или
или 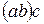 писать просто
писать просто 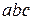 . Эта же аксиома позволяет по индукции доказать, что произведение нескольких сомножителей
. Эта же аксиома позволяет по индукции доказать, что произведение нескольких сомножителей 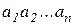 в группе при заданном порядке множителей не зависит от способа расстановки скобок. Этим придается однозначный смысл записи степени
в группе при заданном порядке множителей не зависит от способа расстановки скобок. Этим придается однозначный смысл записи степени 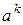 , где
, где 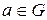 , а
, а 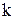 - целый положительный показатель. Удобно считать, что
- целый положительный показатель. Удобно считать, что 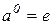 , а для отрицательных целых показателей
, а для отрицательных целых показателей 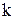 по соглашению
по соглашению 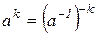 . Равенства
. Равенства 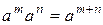 и
и 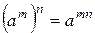 очевидные для положительных показателей, также справедливы в группе для любых целых
очевидные для положительных показателей, также справедливы в группе для любых целых 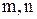 .
.
Далее отметим, что группа  называется конечной, если конечное число всех ее элементов, т. е. множество
называется конечной, если конечное число всех ее элементов, т. е. множество  конечно. В противном случае группа
конечно. В противном случае группа  называется бесконечной. Число элементов конечной группы
называется бесконечной. Число элементов конечной группы  называют ее порядком и пишут
называют ее порядком и пишут 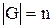 .
.
Говорят, что группа  - группа без кручения, если любой ее неединичный элемент имеет бесконечный порядок. Если же напротив, порядки всех элементов группы
- группа без кручения, если любой ее неединичный элемент имеет бесконечный порядок. Если же напротив, порядки всех элементов группы  конечны, то такая группа называется периодической. Группа, содержащая неединичные элементы как конечного, так и бесконечного порядка, называется смешанной. Если же порядки элементов периодической группы ограничены в совокупности, то их наименьшее общее кратное называется периодом (показателем) группы.
конечны, то такая группа называется периодической. Группа, содержащая неединичные элементы как конечного, так и бесконечного порядка, называется смешанной. Если же порядки элементов периодической группы ограничены в совокупности, то их наименьшее общее кратное называется периодом (показателем) группы.
