Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения

Первого порядка.

Уравнение вида , где - искомая функция, называется обыкновенным дифференциальным уравнением первого порядка. Функция , обращающая уравнение в тождество, называется решением уравнения, а график этой функции – интегральной кривой. Если решение уравнения задано в неявном виде , то оно обычно называется интегралом уравнения. Процесс нахождения решений называется интегрированием дифференциального уравнения.

Уравнение вида , где - заданная функция переменных и 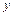, называется ДУ первого порядка, разрешённым относительно производной. Эту форму записи ДУ называют нормальной. Учитывая, что , ДУ первого порядка, разрешённое относительно производной, можно всегда записать в дифференциальной форме: , где и 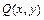- заданные функции переменных и .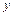

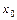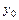Условие , где , -заданные числа, называется начальным условием. Задача нахождения решения уравнения , удовлетворяющего заданному начальному условию , называется задачей Коши.

Общим решением ДУ первого порядка называется решение , зависящее от одной произвольной постоянной , такое, из которого при надлежащем выборе значения постоянной можно получить решение , удовлетворяющее заданному начальному условию . Общее решение, заданное в неявном виде , называется общим интегралом уравнения.

Частным решением ДУ первого порядка называется решение , получаемое из общего при конкретном значении постоянной (при этом не исключаются и значения ). Частное решение, заданное в неявном виде , называется частным интегралом уравнения.

Решение ДУ первого порядка, в каждой точке которого нарушается единственность решения задачи Коши, называется особым. Особое решение не содержится в формуле общего решения ни при каком числовом значении произвольной постоянной, включая . Особое решение всегда можно обнаружить в процессе построения общего решения (общего интеграла) данного ДУ. Это те решения, которые могут быть утеряны при преобразованиях данного уравнения, переводящих это уравнение в его общее решение (общий интеграл).

ДУ вида называется уравнением с разделёнными переменными. Его общий интеграл имеет вид .

ДУ вида или называется уравнением с разделяющимися переменными. Его интегрирование, путём деления обеих частей уравнения на или , сводится (с учётом ) к интегрированию уравнения с разделёнными переменными.

При выполнении деления возможна потеря решений, для которых или . Потерянные решения или содержатся в формуле общего решения при каком-то конкретном значении произвольной постоянной (при этом не исключаются и значения ) или являются особыми решениями.

В задачах 9.1-9.12 найти общие решения следующих ДУ с разделяющимися переменными:

9.1 . 9.2 .

9.3 . 9.4 .

9.5 . 9.6 .

9.7 . 9.8 . 9.9 . 9.10 .

9.11 .

9.12 .

Дифференциальное уравнение вида ( 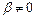) приводится к уравнению с разделяющимися переменными подстановкой , где - новая искомая функция.

В задачах 9.13-9.16найти общие решения уравнений, приводящихся к ДУ с разделяющимися переменными:

9.13 . 9.14 .

9.15 . 9.16 .

Найти частное решение дифференциального уравнения первого порядка – значит: 1) найти его общее решение или общий интеграл ; 2) найти то частное решение (частный интеграл ) которое удовлетворяет заданному начальному условию .

В задачах 9.17-9.22 найти частные решения ДУ, удовлетворяющие указанным начальным условиям:

9.17 , .

9.18 , .

9.19 , .

9.20 , .

9.21 , .

9.22 , .

Дифференциальное уравнение вида или , где и 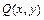- однородные функции одинаковой степени, называется однородным.

Функция , обладающая свойством при всех 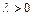, называется однородной функцией степени .

Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой , или , где - новая неизвестная функция. Интегрируя ДУ с разделяющимися переменными относительно функции и возвращаясь к искомой функции 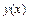, находим общее решение исходного уравнения. Иногда целесообразно вместо подстановки , использовать подстановку , где - новая неизвестная функция.

В задачах 9.23-9.36найти общие решения следующих однородных дифференциальных уравнений:

9.23 . 9.24 .

9.25 . 9.26 .

9.27 . 9.28 .

9.29 . 9.30 . 9.31 . 9.32 .

9.33 . 9.34 .

9.35 . 9.36 .

Уравнение вида приводится к однородному уравнению или уравнению с разделяющимися переменными.

Пусть , тогда:

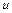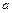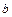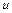1) если , то подстановкой , где и - новые переменные, и - некоторые числа, определяемые из системы уравнений , исходное уравнение приводится к однородному ДУ относительно новых переменных и ;

2)если 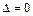, то подстановкой исходное уравнение приводится к уравнению с разделяющимися переменными.

В задачах 9. 37-9.40найти общие решения уравнений:

9.37 . 9.38 .

9.39 .

9.40 .

В задачах 9.41-9.46найти частные решения уравнений, удовлетворяющие указанным начальным условиям:

9.41 , .

9.42 , .

9.43 , . 9.44 , .

9.45 , .

9.46 , .

Уравнение вида называется линейным. Уравнение , в котором правая часть тождественно равна нулю, называется однородным линейным уравнением.

Общее решение неоднородного линейного уравнения находится подстановкой , , где и - неизвестные функции от . Уравнение тогда примет вид . Приравняв нулю выражение в скобках, получим уравнение с разделяющимися переменными , из которого найдём в виде его частного решения , где - какая-нибудь первообразная для . Подставив затем найденное выражение в уравнение , получим уравнение с разделяющимися переменными , из которого найдём в виде его общего решения. В результате найдём и общее решение исходного уравнения в виде .

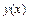Некоторые уравнения становятся линейными, если поменять ролями искомую функцию и независимую переменную. Например, уравнение - нелинейное относительно и , является линейным относительно и : .

В задачах 9.47-9.62 найти общие решения следующих линейных дифференциальных уравнений:

9.47 . 9.48 .

9.49 . 9.50 .

9.51 . 9.52 .

9.53 . 9.54 .

9.55 . 9.56 .

9.57 . 9.58 .

9.59 . 9.60

9.61 . 9.62 .

В задачах 9.63-9.70 найти частные решения уравнений, удовлетворяющие указанным начальным условиям:

9.63 , . 9.64 , .

9.65 , . 9.66 , .

9.67 , .

9.68 , . 9.69 , .

9.70 , .

Уравнение вида , где и , называется уравнением Бернулли. Оно приводится к линейному с помощью подстановки . Решение уравнения Бернулли можно также найти непосредственно подстановкой .

В задачах 9.71-9.78найти общие решения уравнений Бернулли:

9.71 . 9.72 .

9.73 . 9.74 .

9.75 . 9.76 .

9.77 . 9.78 .

Уравнение называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции , т.е. . Это имеет место, если выполнено тождество .

Общий интеграл уравнения имеет вид , где - произвольная постоянная. Функцию находим, используя равенства и . Сначала, интегрируем первое из равенств по и определяем функцию с точностью до произвольной дифференцируемой функции в виде , где 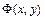- одна из первообразных для функции . Затем, подставляем это выражение для во второе из равенств и получаем дифференциальное уравнение для определения функции : , интегрируя которое находим в виде его частного решения.

В задачах 9.79-9.86решить следующие уравнения, предварительно убедившись, что они являются уравнениями в полных дифференциалах:

9.79 .

9.80 .

9.81 . 9.82 .

9.83 .

9.84 .

9.85 ; .

9.86 ; .

Уравнения первого порядка , не разрешённые относительно производной, решают следующими методами.

1)Разрешаем уравнение относительно и получаем одно или несколько уравнений вида ( ), каждое из которых надо решить. Если решение уравнений найдено в виде общих интегралов , то общий интеграл исходного уравнения записываем в виде .

2)Метод введения параметра. Разрешаем уравнение относительно 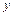и записываем в виде . Вводим параметр и получаем . Берём полный дифференциал от обеих частей равенства и заменяя через , получаем уравнение вида . Если решение этого уравнения найдено в виде , то учитывая равенство , записываем решение исходного уравнения в параметрическом виде: , . Уравнения вида решают таким же способом.

В задачах 9.87-9.92разрешить следующие уравнения относительно и найти их общее решение:

9.87 . 9.88 .

9.89 . 9.90 .

9.91 . 9.92 .

В задачах 9.93-9.98найти общие решения следующих уравнений методом введения параметра:

9.93 . 9.94 .

9.95 . 9.96 .

9.97 . 9.98 .

В задачах 9.99-9.120найти общие решения следующих дифференциальных уравнений первого порядка:

9.99 . 9.100 .

9.101 . 9.102 .

9.103 . 9.104 .

9.105 . 9.106 .

9.107 . 9.108 .

9.109 . 9.110 .

9.111 . 9.112 .

9.113 . 9.114 .

9.115 . 9.116 .

9.117 . 9.118 .

9.119 . 9.120 .

Для решения геометрических задач, надо построить чертёж, обозначить искомую кривую через (если задача решается в прямоугольных координатах) и выразить все упоминаемые в задаче величины через , 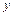и . В результате получим дифференциальное уравнение, из которого найдём искомую функцию 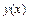. При решении геометрических задач часто используют геометрический смысл производной как тангенса угла, образованного касательной к кривой с положительным направлением оси .

В физических задачах при составлении дифференциальных уравнений используют физический смысл производной (если независимая переменная – время 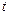, то - скорость изменения величины 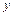), а также физические законы, сформулированные в тексте задачи.

В задачах 9.121-9.128найти решения, предварительно составив дифференциальное уравнение.

9.121 Найти кривые, у которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, вдвое меньшую абсциссы точки касания.

9.122Найти кривые, у которых площадь треугольника, ограниченного касательной, осью абсцисс и отрезком от начала координат до точки касания, есть величина постоянная, равная .

9.123Найти атмосферное давление на высоте , если на поверхности Земли давление равно и плотность воздуха (Указание:использовать закон Бойля-Мариотта, согласно которого плотность пропорциональна давлению).

9.124 Тело охладилось за 10 мин от С до С. Температура окружающего воздуха поддерживается равной С. Когда тело остынет до С? (Указание: принять, что скорость остывания тела пропорциональна разности температур тела и окружающей среды).

9.125На материальную точку массы действует постоянная сила, сообщающая точке ускорение . Окружающая среда оказывает движущейся точке сопротивление, пропорциональное скорости её движения, коэффициент пропорциональности равен . Как изменяется скорость движения со временем, если в начальный момент точка находилась в покое? (Указание: воспользоваться вторым законом Ньютона ).

9.126Материальная точка движется по прямой со скоростью, обратно пропорциональной пройденному пути. В начальный момент точка находилась на расстоянии от начала отсчёта пути и имела скорость . Определить пройденный путь и скорость точки через секунд после начала движения.

9.127Имеется некоторое количество радиоактивного вещества. Известно, что через дней распадается 50% этого вещества. Через сколько дней останется 1% начального количества вещества? (Указание: из эксперимента известно, что скорость радиоактивного распада пропорциональна количеству вещества).

9.128Скорость обесценивания оборудования вследствие его износа пропорциональна в каждый момент времени его фактической стоимости 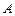. Начальная стоимость оборудования равна . Найти стоимость оборудования по истечении лет.

9.129Численность населения некоторого города удовлетворяет уравнению , где -время (в годах). В начальный момент население города составляло 10 тысяч человек. Через сколько лет население увеличится в 10 раз?

9.130Функции спроса и предложения на некоторый товар имеют вид: и . Найти зависимость равновесной цены от времени , если в начальный момент времени цена ден.ед.

Обыкновенные дифференциальные уравнения

Высших порядков.

Уравнение вида , где - искомая функция, называется дифференциальным уравнением -го порядка. Функция , обращающая уравнение в тождество, называется решением уравнения, а график этой функции – интегральной кривой. Если решение уравнения задано в неявном виде , то оно называется интегралом уравнения.

Уравнение вида , называется уравнением, разрешённым относительно старшей производной. Эту форму записи ДУ -го порядка называют нормальной.

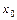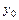Условия , ,…, , где , , ,…, - заданные числа, называются начальными условиями. Задача нахождения решения уравнения , удовлетворяющего заданным начальным условиям, называется задачей Коши.

Общим решением ДУ -го порядка называется решение , зависящее от произвольных постоянных 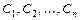, такое, из которого при надлежащем выборе значений постоянных 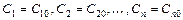можно получить решение , удовлетворяющее заданным начальным условиям , ,…, . Общее решение, заданное в неявном виде , называется общим интегралом уравнения.

Частным решением ДУ -го порядка называется решение , получаемое из общего при конкретных значениях постоянных 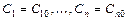. Частное решение, заданное в неявном виде , называется частным интегралом уравнения.

Если для искомого частного решения уравнения заданы начальные условия , ,…, и известно общее решение уравнения, то значения произвольных постоянных определяются, если это возможно, из системы уравнений .

Уравнение вида называется простейшим дифференциальным уравнением -го порядка. Его общее решение находят, выполняя последовательно интегрирований, и записывают в виде

.

Уравнение вида , , не содержащее явно искомой функции 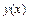, с помощью подстановки , где - новая неизвестная функция, приводится к уравнению порядка .

Уравнение вида , не содержащее явно независимой переменной , с помощью подстановки , где - новая неизвестная функция от новой независимой переменной 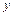, приводится к уравнению порядка на единицу ниже. При этом преобразуются так: , ,…..

В задачах 9.131-9.150 найти общие решения дифференциальных уравнений,допускающих понижение порядка:

9.131 . 9.132 . 9.133 .