Тема 1.3 Графическое решение системы уравнений.

Системы уравнений с двумя неизвестными могут быть приближенно решены графически. Их решением являются координаты точки пересечения линий, соответствующих уравнениям системы. При этом точность решения будет определяться величиной шага дискретизации (чем шаг меньше, тем точность выше). Рассмотрим примеры графического решения системы двух уравнений.

Пример.

Пусть необходимо найти решение системы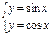

в диапазоне 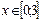с шагом D=0,2.

Решение.

Ввести данные в рабочую таблицу. В ячейку А1 ввести слово Аргумент. Начиная с ячейки А2 в столбец ввести значения х. В ячейку В1 ввести слово Синус. Далее в ячейку В2 для получения значения синуса воспользуемся специальной функцией (Вставка - Функция). В появившемся диалоговом окне Мастера функций – шаг 1 из 2 в поле Категория выбираем Математические. Выбираем функцию SIN. Нажимаем кнопку ОК. Появляется диалоговое окно функции SIN. Указываем значение аргумента при помощи щелчка на ячейке А2. Нажимаем ОК. В ячейке В2 появилось значение функции. Теперь при помощи Маркера заполнения «размножим» функцию, находящуюся в ячейке В2. Аналогично получаем значение косинуса. Далее необходимо построить диаграмму кривых синуса и косинуса. Как видно из диаграммы система имеет одно решение (есть точка пересечения), и оно на заданном интервале единственное. Таким образом, решением системы в заданном диапазоне являются координаты точки пересечения кривых. Для их нахождения необходимо навести указатель мыши на точку пересечения и щелкнуть левой кнопкой мыши. Появляется надпись с указанием искомых координат. 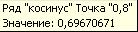. Таким образом приближенное решение системы х=0,8, у=0,697.

Упражнения.

1. Построить прямую 3x+2y-4=0 в диапазоне 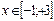с шагом D=0,25.
2. Построить прямую, проходящую через точки А(0;3) и B(2;2) в диапазоне 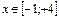с шагом D=0,5.
3. Построить прямую, проходящую через точки начало координат и точку B(2;3) в диапазоне 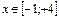с шагом D=0,25.
4. Построить параболу y=2x²-1 в диапазоне хÎ[0;4] с шагом 0,25.
5. Графически решить систему 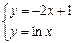в диапазоне 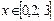с шагом D=0,2.
6. Графически решить систему 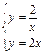в диапазоне 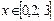с шагом D=0,2.

Тема 1.4 Использование программы Excel в линейной алгебре

Цель занятия: Научиться производить операции с матрицами в Excel.

Матрицей размера m*n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы и обозначаются строчными буквами с двойной индексацией: 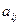, где i – номер строки, j – номер столбца. Например,

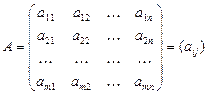
Операции с матрицами.

Транспонирование

Транспонированной (обратной) называется матрица, в которой столбцы исходной матрицы заменяются строками с соответствующими номерами. Исходная матрица: А = (а_ij), транспонированная – А^т = ( а_ji).

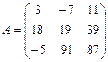
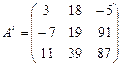
Для осуществления транспонирования в Excel используется функция ТРАНСП в категории Ссылки и массивы, которая позволяет менять ориентацию массива. Функция имеет вид ТРАНСП(массив). Массив – это диапазон ячеек на рабочем листе, в котором записаны элементы матрицы.

Пример 1. Дана матрица А, получить транспонированную матрицу А^т.

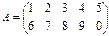
Решение.

1. Введите на рабочий лист Excel предложенную матрицу (в ячейку число). Выделите указателем мыши блок ячеек под транспонированную матрицу (размер транспонированной матрицы: количество строк = количеству столбцов в исходной матрице). В данном случае размер исходной матрицы 2*5, транспонированной – 5*2 .

2. Меню Вставка – Функция, в появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите Ссылки и массивы, в рабочем поле функции – имя функции ТРАНСП.

3. В окне ТРАНСП укажите диапазон ячеек исходной матрицы. После чего нажмите сочетание клавиш CTRL+SHIFT+ENTER.

4. В указанном вами диапазоне должна появиться транспонированная матрица.