Потенциальная энергия деформации

Уравнение для потенциальной энергии деформации многослойной оболочки имеют вид

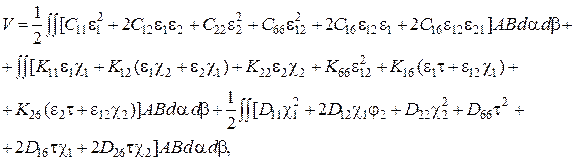(2.28)

где коэффициенты 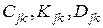имеют вид

;

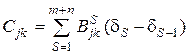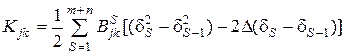; (2.29)

.

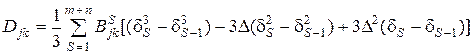В частном случае, когда координатная поверхность оболочки совпадает с нижней поверхностью оболочки, 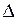превращается в нуль (рис.2.4), в связи с чем существенным образом упрощаются выражения (2.29), т.е.

;

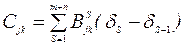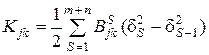; (2.30)

.

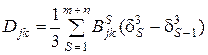В уравнении (2.28) первая составляющая представляет потенциальную энергию удлинений и сдвигов, третье – изгибов и кручений, а второе – взаимное влияние изгибов, кручений. удлинений и сдвигов.

Коэффициенты 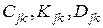называются жесткостями:

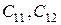– жесткости растяжения – сжатия по координатным линиям , ;

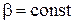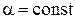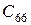– жесткость сдвига в плоскости, касательной к координатной поверхности;

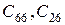– побочные жесткости растяжения – сжатия и сдвига, характеризующие влияние удлинений по координатным линиям 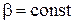, 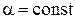на сдвиг в касательной плоскости;

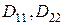– жесткости изгиба вокруг осей, касательных к координатным линиям , ;

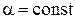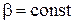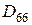– жесткость кручения;

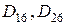– побочные жесткости изгиба и кручения, характеризующие влияние изгибов осей, касательных к координатным линиям 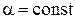, 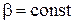на кручение;

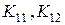–жесткости взаимного влияния растяжения и изгиба, характеризующие взаимное влияние растяжения и изгиба по линиям , ;

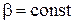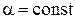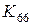– жесткость взаимного влияния кручения и сдвига;

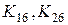– побочные жесткости взаимного влияния изгибов на сдвиг и удлинений на кручение, соответственно.

Соотношения упругости

Уравнения, которые устанавливают связь между внутренними усилиями и деформациями координатной поверхности оболочки, называются соотношениями упругости. Для общего случая многослойной анизотропной оболочки они имеют вид

;

;

(2.31)

;

;

;

.

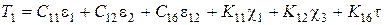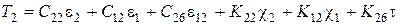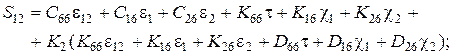
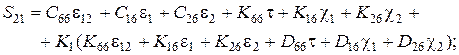
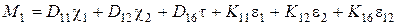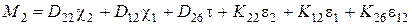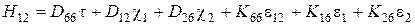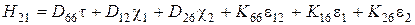Уравнения для 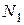и 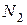не будем приводить, так как при наличии известных соотношений упругост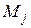и и 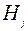эти поперечные силы могут быть получены из четвертого и пятого уравнений равновесия (2.27).

Граничные условия

В реальных шахтных объектах можно встретиться с самыми разнообразными типами опор оболочек и это многообразие решений опор невозможно представить в виде каких-либо математических моделей – граничных условий. В связи с этим приведем лишь некоторые возможные варианты граничных условий.

Ради краткости записи граничных условий приводим лишь для края, который определяется координатной линией .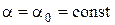

1. Однородные граничные условия:

А) свободный край

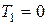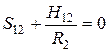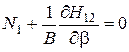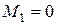, , , ; (2.32)

Б) шарнирно-закрепленный край

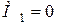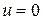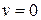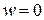, , , ; (2.33)

В) шарнирный, свободный в тангенциальном направлении край

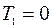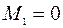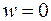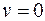, , , ; (2.34)

или 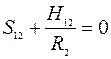, , 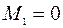, 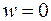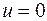; (2.35)

Г) шарнирный, свободный в нормальном направлении край

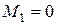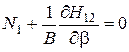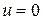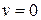, , , ; (2.36)