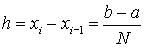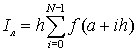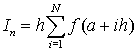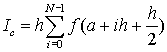I.I Интегрирование методом прямоугольников (метод Эйлера)

Расчетно-графическая работа

по дисциплине Математика

на тему Приближенные методы интегрирования

Вариант №1

Выполнила:

студентка группы МС-41-14

Алякина М.И.

Преподаватель:

Селиверстова Л.В.

Чебоксары 2015

Введение

Перейдем теперь к некоторым употребительным методам приближенного интегрирования, позволяющим находить приближенное значение определенного интеграла от любой непрерывной функции с практически достаточной точностью. Потребность в приближенном вычислении интеграла может возникнуть и тогда, когда не существует или неизвестен метод отыскания точного значения интеграла, и тогда, когда этот метод известен, но неудобен. Излагаемые приближенные численные методы основаны на следующем: рассматривая интеграл как площадь криволинейной трапеции, мы получим ее приближенное значение, т.е. приближенное значение интеграла, если вычислим площадь другой трапеции, ограничивающая линия которой по возможности мало отклоняется по положению от заданной линий. Вспомогательную линию при этом проводим так, чтобы получилась фигура, площадь которой легко вычисляется.
Дадим следующие правила численного интегрирования:

1) правило прямоугольников и правило трапеций;

2) правило параболических трапеций, называемое по имени его автора правилом Симпсона.

Ъ I. Правило прямоугольников и правило трапеций.

I.I Интегрирование методом прямоугольников (метод Эйлера).

Пусть функцию (рисунок справа) необходимо проинтегрировать численным методом на отрезке [a, b]. Разделим отрезок на Nравных интервалов (на рисунке N = 4).

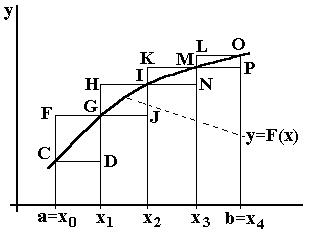Площадь каждой из 4-х криволинейных трапеций можно заменить на площадь прямоугольника.

Ширина всех прямоугольников одинакова и равна

Рис. 1

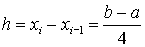
В качестве выбора высоты прямоугольников можно предложить выбрать значение функции на левой границе. В этом случае высота первого прямоугольника составит f(a),второго – f(x₁), третьего – f(x₂), последнего – f(x₃). Приближенное значение интеграла получается суммированием площадей прямоугольников

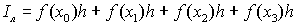
Если в качестве выбора высоты прямоугольников взять значение функции на правой границе, то в этом случае высота первого прямоугольника составит n f(x1), второго – f(x2) – f(x3), последнего f(b).

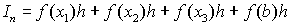
Как видно, в этом случае, одна из формул дает приближение к интегралу с избытком, а вторая с недостатком. Можно предложить еще один способ, очевидно лучший, чем обе эти формулы – использовать для аппроксимизации значение функции в середине отрезка интегрирования.

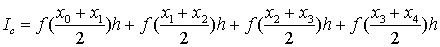
В общем виде, если отрезок [a,b] разбить на N равных интервалов интегрирования (h) и к каждому интервалу применить формулу прямоугольников, то получим: