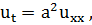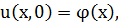Уравнение теплопроводности
Рассмотрим ограниченный объем V, в котором идет процесс выделения тепла. В нем существует процесс теплопередачи и есть источник тепла 
.
Пусть q – удельная тепловая мощность: 
Количество теплоты, выделившееся в объеме за время Δt будет равно:
Рис.19
Так как 
только на 
, то область интегрирования можно расширить до объема V. Пусть 
– плотность тела, c – удельная теплоемкость.
Тогда количество теплоты, идущее на нагрев V:
где 
– перепад температуры.
Введем функцию 
– температура в точке 
в момент времени t. Тогда:
Если температура тела неравномерна, то в нем возникают тепловые потоки, направленные из мест с более высокой температурой в места с более низкой. Из закона теплопроводности Фурье:
– количество теплоты, перетекающее через элемент поверхности dS за время 
,
где 
– нормаль к поверхности S, k – коэффициент теплопроводности.
Используем теорему Гаусса-Остроградского:
Уравнение теплового баланса r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
дает
Объем V был выбран произвольно. Следовательно, равенство интегралов равносильно равенству подынтегральных выражений.
При 
, 
получаем
Если k=const, то 
(3.1) – уравнение теплопроводности, где 
.
(3.1) – дифференциальное уравнение параболического типа. В одномерном случае u=u(x,t). Тогда (3.1) принимает вид:
(3.1’)
Само дифференциальное уравнение неоднородно. Если 
, то в системе есть подкачка тепла извне, а если 
, то подкачки нет, и в системе осуществляется охлаждение.
Построим простейшие краевые задачи.
1. Охлаждение бесконечного стержня:
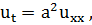
2. Охлаждение полубесконечного стержня, левый конец стержня поддерживается при нулевой температуре:
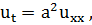
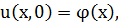
3. Полубесконечный стержень, через левый край которого нет теплопередачи:
,
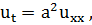
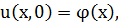
s New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>=0.</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
4. Краевая задача для конечного стержня, оба конца которого поддерживаются при нулевой температуре:
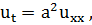
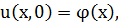
5. Наиболее общая краевая задача имеет вид:
