Нормальное уравнение плоскости – описание и пример

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz.

Рассмотрим плоскость, которая удалена на расстояние p ( 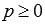) единиц от начала координат в положительном направлении нормального вектора плоскости 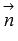. Будем считать, что длина вектора 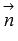равна единице. Тогда его координаты равны направляющим косинусам, то есть, 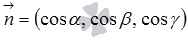, причем 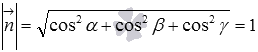. Обозначим расстояние от точки до плоскости как 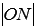, то есть, точка N лежит на плоскости и длина отрезка ONравна p. Для наглядности отметим все данные на чертеже.

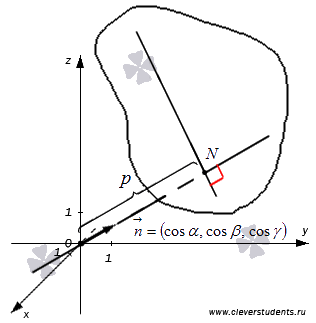
Получим уравнение этой плоскости.

Возьмем точку трехмерного пространства 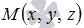. Тогда ее радиус вектор 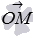имеет координаты 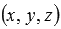, то есть, 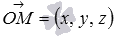(при необходимости смотрите разделкоординаты радиус-вектора точки). Очевидно, что множество точек 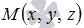определяют описанную ранее плоскость тогда и только тогда, когда числовая проекция вектора 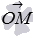на направление вектора 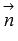равна p, то есть, 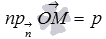(смотрите рисунок ниже).

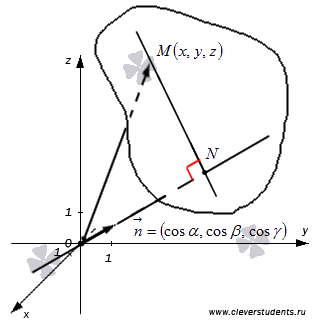
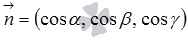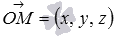Тогда определение скалярного произведения векторов и дает нам следующее равенство 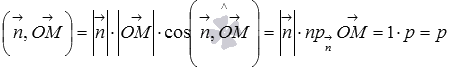. Это же скалярное произведение в координатной форме представляется как 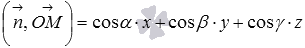. Сопоставление двух последних равенств дает нам искомое уравнение плоскости 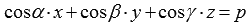. Перенесем p в левую часть, и мы получим уравнение 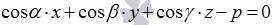, которое называется нормальным уравнением плоскости или уравнением плоскости в нормальном виде. Нормальное уравнение плоскости иногда называют нормированным уравнением плоскости.

Итак, нормальное уравнение плоскости вида 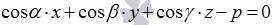задает в прямоугольной системе координат Oxyz плоскость, удаленную от начала координат на расстояние p в положительном направлении единичного нормального вектора плоскости .

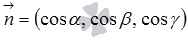Следует заметить, что косинусы зачастую явно не фигурирует в нормальном уравнении плоскости, так как 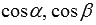и 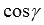- это некоторые действительные числа, сумма квадратов которых равна единице.

Приведем пример нормального уравнения плоскости.

Пусть плоскость задана в прямоугольной системе координат Oxyz уравнением в нормальном виде 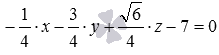. Здесь 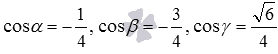, нормальный вектор плоскости 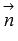имеет координаты 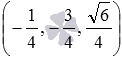, его длина равна единице, так как 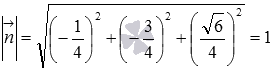. Более того, заданная плоскость находится на расстоянии 7 единиц от начала координат в направлении вектора 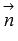, так как p = 7.

Очевидно, что нормальное уравнение плоскости представляет собой общее уравнение плоскости вида 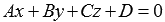, в котором числа A, B и C таковы, что длина нормального вектора плоскости 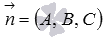равна единице, а число D неотрицательно.

Осталось разобраться с вопросом: «Как узнать, действительно ли перед нами нормальное уравнение плоскости»? Ответить на него достаточно просто: если выполняются оба условия 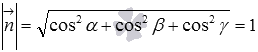и 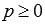, то мы имеем уравнение плоскости в нормальном виде, если же хотя бы одно из условий не выполняется, то уравнение плоскости не является нормальным. Рассмотрим пример.

Пример.

Есть ли среди указанных уравнений уравнения плоскости в нормальном виде?

· ;

· ;

· .

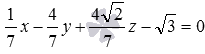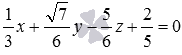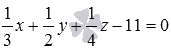Решение.

Начнем с первого уравнения. Проверим, равна ли длина нормального вектора плоскости 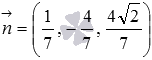единице. Вычислим длину: 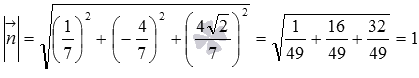. Осталось убедиться, что числоp в этом уравнении положительно. Это действительно так, так как 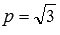. Таким образом, первое уравнение плоскости является уравнением плоскости в нормальном виде.

Второе уравнение плоскости не является нормальным уравнением плоскости, так как не выполняется условие 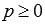(в этом уравнении ).

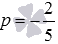В третьем уравнении длина нормального вектора 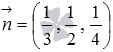не равна единице: 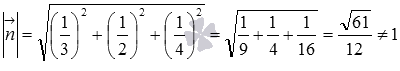. Поэтому оно не является уравнением плоскости в нормальном виде.

Ответ:

только первое уравнение является нормальным уравнением плоскости.