Геометрический смысл модуля и аргумента производной

Лекция №1.

Понятие области, односвязной области, кривой Жордана. Геометрический смысл аргумента и модуля производной; понятие конформного отображения. Конформные отображения посредством дробно-линейной функции.

Теоретические вопросы:

1. Понятие области, односвязной области, кривой Жордана.

2. Геометрический смысл аргумента и модуля производной;

3. Понятие конформного отображения.

Содержание лекции

Комплексными числами и функциями комплексного переменного математики пользовались в своих исследованиях уже в XVIII веке. Особенно велики заслуги крупнейшего математика XVIII века Леонарда Эйлера, который по праву считается одним из творцов теории функций комплексного переменного и начала интегрального исчисления функций комплексного переменного.

Геометрическая теория функций комплексного переменного изучает аналитические функции, определяемые каким-либо геометрическим свойством, а также различные геометрические свойства тех или иных классов аналитических функций. Поэтому естественно, что она опирается на ряд общих геометрических понятий, встречающихся в современной математике.

Ниже будут изложены основные определения и факты, относящиеся к понятию комплексных чисел, действия с ними и их геометрической интерпретации.

Множества точек на плоскости. Множества точек на плоскости будем обозначать большими буквами; точки же плоскости обозначаем малыми буквами, а именно теми же буквами, что и соответствующие им комплексные числа.

Если точка а принадлежит множеству Е, то это записывается так: 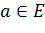. Если все точки множества Е принадлежат множеству F, то пишут 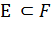и называют E множеством, лежащим в F, или частью F.

Каждой точке плоскости приписываются окрестности. Под окрестностью данной точки а понимается совокупность всех внутренних точек какого-либо круга с центром в а (а иногда и любое множество точек, содержащее в себе такую круговую окрестность). Окрестность называется достаточно малой, если радиус круга достаточно мал.

Множество точек называется ограниченным, если оно целиком лежит внутри некоторого круга.

Точка а плоскости называется предельной точкой или точкой сгущения данного множества, если в любой окрестности а имеются точки множества, отличные от а. Предельная точка может принадлежать, а может и не принадлежать множеству. Точка множества, не являющаяся его предельной точкой, называется изолированной точкой множества.

Если данная точка а предельная для некоторого множества, то из него можно выделить последовательность точек, сходящуюся к а.

Последовательность точек может сходиться и к бесконечно далекой точке. Для того чтобы последовательность сходилась к конечной точке, необходимо и достаточно, чтобы расстояние между любыми двумя точками этой последовательности, начиная с некоторого номера, было меньше любого данного положительного числа.

Множество точек называется замкнутым, если ему принадлежат все его предельные точки. Любое множество можно сделать замкнутым, если к нему присоединить все его предельные точки. Так полученное из множества Е замкнутое множество обозначается через 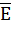и называется замыканием множества Е.

Расстоянием между двумя множествами без общих точек называется точная нижняя граница расстояний любых пар точек, взятых по одной из каждого множества.

Замкнутое множество, состоящее более чем из одной точки, называется континуумом, если оно не распадается на два непустых замкнутых множества без общих точек.

Точка некоторого множества называется внутренней для него, если вместе с ней этому множеству принадлежит и некоторая окрестность этой точки.

Наряду с замкнутыми множествами рассматриваются открытые множества — это множества, состоящие только, из внутренних точек. Очевидно, дополнение к замкнутому множеству на плоскости есть открытое множество, а дополнение к открытому — замкнутое.

Области и кривые. Одним из основных геометрических понятий теории функций комплексного переменного является понятие области.

Областью называется открытое множество, любые две точки которого можно соединить некоторой ломаной линией, целиком состоящей из точек этого множества (свойство связности). Граничными точками области называются точки плоскости, не принадлежащие области, но являющиеся для нее предельными точками.

Совокупность всех граничных точек области образует границу области. Граница области есть замкнутое множество. Точки плоскости, не являющиеся для области ни внутренними ни граничными точками, называются ее внешними точками. У каждой внешней точки области существует окрестность, не содержащая точек области.

Если к области присоединить ее границу, то полученное множество называется замкнутой областью. В отличие от замкнутой области, сама область иногда называется открытой областью.

Область называется односвязной, если ее граница состоит из континуума или из одной точки или же она является полной плоскостью.

В противном случае область называется многосвязной. Область будет двухсвязной, трехсвязной, n-связной, если ее граница состоит соответственно из двух, трех, континуумов без общих точек; все вместе такие области называются конечносвязными.

Наряду с областью, другим основным геометрическим объектом в теории функций комплексного переменного является функция и кривая.

Говорят, что на множестве M точек плоскости Z задана функция

.

если указан закон, по которому каждой точке 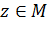ставится в соответствие определенная точка или совокупность точек 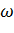. В первом случае функция называется однозначной, во втором – многозначной.

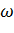Множество M называется множеством определения функции , а совокупность N всех значения , которые принимает на M, – множеством её изменения.

Если положить 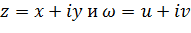, то задание функции комплексного переменного будет равносильным заданию двух функций двух действительных переменных.

.

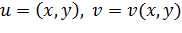Условимся откладывать значение на одной комплексной переменной, а значение 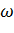– на другой. Тогда функцию комплексного переменного можно геометрически представлять как некоторое отображение множества M плоскости Z на множество N плоскости .

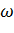Если функция однозначна на области M и при этом двум различным точкам M всегда соответствуют различные точки N, то такое отображение называется взаимно однозначным или однолистным в M.

Пусть дана функция , осуществляющая множества M на множество N. Функция 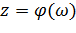, ставящая в соответствие каждой точке 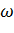из N совокупность всех точек , которые функцией отображаются в точку 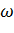, называется обратной к функции .

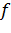Ясно, что отображение будет взаимно однозначным, тогда и только тогда, когда обе функции и 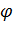однозначны.

Пусть функция отображает множество M на N, а 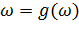множество N на P. Функция 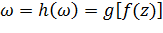, отображающая M на P, называется сложной функцией, составленной из f и g, а соответствующее отображение h – суперпозицией отображений f и g. Если, в частности, отображение взаимно однозначно и функция 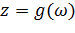– обратная к f, то .

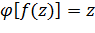Функция называется непрерывной в точке , если она определена в точке и некоторой её окрестности и, если .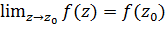

Функция называется непрерывной в области 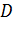, если она непрерывна в каждой точке этой области.

Функция двух переменных, удовлетворяющая уравненям Лапласа 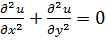или 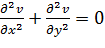называют гармонической.

Если взять за 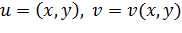две произвольные гармонические функции, то функция 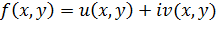в общем случае не будет аналитической в области.

В случае если функция 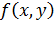аналитическая, то функци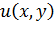и и 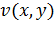называют сопряженными или сопряженными гармоническими функциями.

Непрерывной кривой называется множество точек плоскости, прямоугольные координаты х, у которых могут быть заданы как непрерывные функции 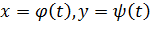вещественного переменного t в некотором конечном промежутке .

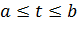Но непрерывная кривая — понятие слишком общее. Существуют непрерывные кривые, которые совершенно не соответствуют наглядному представлению о кривой, как об одномерной фигуре. Так, можно построить непрерывную кривую, проходящую через каждую точку данного квадрата. Однако, если потребовать, чтобы кривая не имела кратных точек, то в этом случае она уже будет обладать рядом наглядных свойств. Такие кривые называются простыми кривыми или кривыми Жордана.

Итак, непрерывная кривая 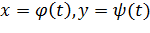или, короче, кривая

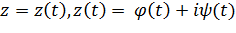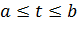, (1)

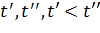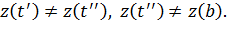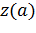называется кривой Жордана, если для любых двух различных значений , из [a, b) имеем Точки и 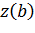могут как совпадать, так и быть различными. В первом случае кривая называется замкнутой, во втором незамкнутой.

Из незамкнутых кривых Жордана можно составить непрерывные кривые и не жорданова типа. С другой стороны, и кривая Жордана иногда оказывается понятием слишком общим и тогда для различных целей вводятся кривые более частных типов, как например, гладкие, кусочногладкие, спрямляемые кривые.

Кривая (1) называется гладкой, если в 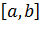существует производная 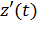(на концах односторонняя), непрерывная и отличная от нуля. Требование гладкости кривой, очевидно, равносильно требованию существования касательной к кривой и непрерывного вращения этой касательной при движении по кривой. Кривая, составленная из конечного числа гладких кривых, называется кусочногладкой кривой.

Наконец, простейший тип непрерывной кривой — аналитическая кривая; эта кривая определяется уравнением 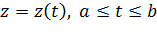, где 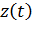вблизи каждого значения 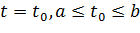, разлагается в сходящийся степенной ряд 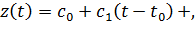с 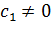. Непрерывную кривую, составленную из конечного числа аналитических кривых, назовем кусочноаналитияеской кривой.

Иногда в области приходится проводить разрезы по различным кривым Жордана. Провести в области B разрез по кривой Жордана 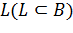значит удалить из B все точки кривой L.

Разрез в области B называется поперечным, если он соединяет две (различные или совпадающие) граничные точки области B, являющиеся его концами, и остальными своими точками лежит в B. Оказывается, что любой поперечный разрез в конечносвязной области, соединяющий граничные точки, лежащие на различных граничных континуумах, не разделяя области на части, уменьшает связность области на единицу; любой же поперечный разрез в односвязной области делит ее на две односвязных области (характеристическое свойство односвязных областей).

Аналогично, разрез, представляющий замкнутую кривую Жордана, целиком лежащую в области B, называется круговым разрезом. Круговой разрез всегда делит область B на две области; в случае односвязной области B одна из областей, ограниченных круговым разрезом, целиком лежит в B (тоже характеристическое свойство односвязных областей).

Наконец, разрез, представляющий открытую кривую Жордана, лежащую в какой-либо области B целиком или исключая один из своих концов, не делит B на части.

Многие разделы теории функций комплексного переменного и, в частности, геометрическая теория функций широко используют в своих доказательствах особые свойства сходимости последовательностей аналитических функций. Благодаря этим свойствам доказательства довольно просты и изящны по сравнению с аналогичными доказательствами вещественного анализа.

Введем следующие определения. Пусть имеется последовательность однозначных функций 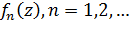определенных на некотором множестве 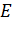точек плоскости .

Определение. Последовательность называется сходящейся в точке 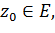если последовательность чисел 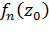сходится.

Определение. Последовательность функций 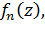называется сходящейся на 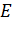, если она сходится во всех точках множества .

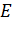В этом случае можно говорить о предельной функции 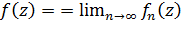определенной на .

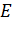Определение. Последовательность 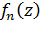называется равномерно сходящейся на 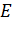к функции 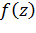, конечной на 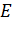, если для каждого 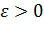существует 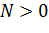такое, что при 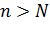имеем 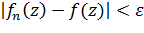для всех .

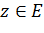Если же 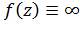на 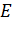, то последовательность 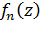по определению равномерно сходится на 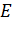к 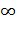, если для каждого 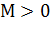существует 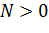такое, что при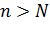 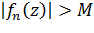для всех 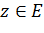. Легко доказать, что для равномерной сходимости последовательности к конечной функции необходимо и достаточно, чтобы для каждого 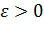существовало такое 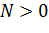, что при 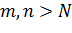и для всех 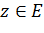выполнялось неравенство .

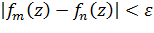Если функции 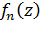определены в области 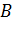, то кроме понятия равномерной сходимости последовательности в области 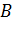можно рассматривать равномерную сходимость последовательности внутри области 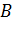, что означает равномерную сходимость 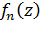на каждом замкнутом множестве 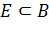. Равномерная сходимость внутри 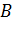– требование более слабое, чем равномерная сходимость в .

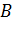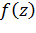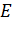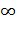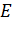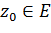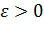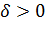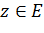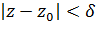Определение. Функция , однозначная и конечная на множестве , не содержащем , называется непрерывной на , если, для любой точки , для любого существует такое, что если и , то 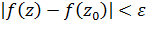. Для последовательностей непрерывных и аналитических функций имеет место ряд теорема, которые будут рассматриваться ниже.

Геометрический смысл модуля и аргумента производной