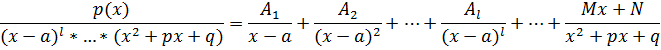Метод наименьших квадратов
На практике часто приходится решать задачи по сглаживанию экспериментальных зависимостей
Пусть существует зависимость для 2-х переменных, выраженная с помощью таблицы, полученной экспериментально
X 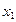 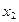 … … 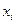 … … 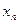 |
Y 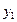 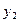 … … 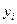 … … 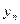 |
Требуется наилучшим образом сгладить экспериментальную зависимость между переменными х и у, т.е. установить зависимость между х и у в виде формулы y = f(x).
Формулы, служащие для аналитических представлений экспериментальных данных, называются эмпирическими.
Задача нахождения эмпирических формул разбивается на 2 этапа.
I этап. Устанавливается вид зависимости y = f(x) (линейная, квадратичная, логарифмическая и т.д.).
II этап. Определяется неизвестные параметры этой функции
Для этого применяют наиболее распространенный и теоретически обоснованный метод наименьших квадратов.
Он состоит в следующем:
В качестве неизвестного параметра функции f(x) выбирают такие значения, чтобы суммы квадратов невязок ( 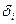 ) была минимальной.
) была минимальной.
Невязка ( 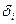 ) – это отклонение от «теоретических» значений
) – это отклонение от «теоретических» значений 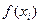 найденных по эмпирическим формулам y = f(x) от соответствующих опытных значений
найденных по эмпирическим формулам y = f(x) от соответствующих опытных значений 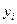 .
.
Рассмотрим функцию 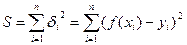 (т.е. сумму квадратов всех невязок).
(т.е. сумму квадратов всех невязок).
Пусть в качестве функций у = f(x) взята линейная функция у = ax + b. Тогда задание сводится к отыскиванию параметров a и b, при которых функция 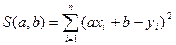
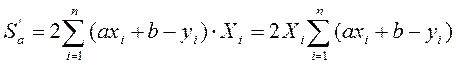 =0
=0
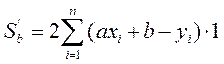
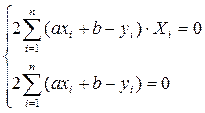
После преобразований, система принимает вид:
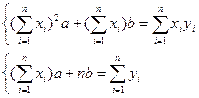
Первообразная и неопределённый интеграл.
Пусть функции f(x) и F(x) определены на интервале (a;b). Если функция F(x) имеет производную на интервале (a;b) и для всех x ? (a;b) выполняется равенство F’(x) = f(x), то функция F(x) называется первообразной функции f(x) на интервале (a;b).
Совокупность всех первообразных функции f(x) на интервале (a;b) наз. неопределенным интегралом от функции f(x) на этом интервале и обозначается
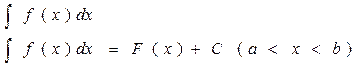
Теорема. 2 первообразные одной и той же ф-ции отличаются на постоянные слагаемые.
15. Свойства неопределённого интеграла.
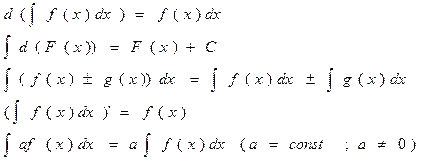
Интегрирование рациональных дробей.
Рацион.ф-цией назыв. ф-ция R(x), кот. явл. отношением двух многочленов.
Теорема. Любой многочлен с действ.коэффициентами степени≥2 представим в виде произведения сомножителей линейных и квадратичных вида 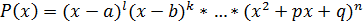 .
.
Интегрирование неправ.рац.дробей сводится к интегрированию прав.рац.дробей.
Метод сведения интеграла к интегралу от рац.дроби назыв. методом рационализации.
Интегрирование правильных рациональных дробей.
Прав.рац.дробь вида 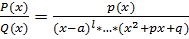 можно представить в виде суммы простейших рац.дробей.
можно представить в виде суммы простейших рац.дробей.