Предел функции нескольких переменных
Раздел 6. Дифференциальное исчисление функции нескольких переменных
Предел и непрерывность функции нескольких переменных
- Понятие функции нескольких переменных
При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты остаются справедливыми для функций произвольного числа переменных.
Пусть дано множество 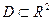 , и пусть указано правило (закон), по которому каждой точке
, и пусть указано правило (закон), по которому каждой точке 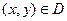 ставится в соответствие единственное действительное число
ставится в соответствие единственное действительное число 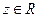 . В этом случае говорят, что задана функция
. В этом случае говорят, что задана функция 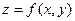 с областью определения
с областью определения  и областью значений
и областью значений 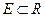 . При этом
. При этом 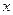 и
и 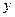 называют независимыми переменными (аргументами), а
называют независимыми переменными (аргументами), а 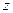 – зависимой переменной (функцией).
– зависимой переменной (функцией).
Функцию 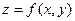 иногда записывают в виде
иногда записывают в виде 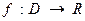 .
.
Пример. На множестве 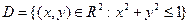 определим функцию
определим функцию 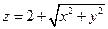 ; тогда ее областью значений является отрезок
; тогда ее областью значений является отрезок 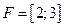 . Эту функцию можно определить, конечно, и на всей плоскости
. Эту функцию можно определить, конечно, и на всей плоскости 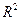 ; в этом случае имеем
; в этом случае имеем 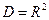 и
и 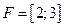 .
.
Графиком функции 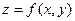 называют множество точек пространства
называют множество точек пространства 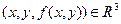 . Обычно графиком функции является некоторая поверхность.
. Обычно графиком функции является некоторая поверхность.
Расстоянием между двумя произвольными точками 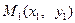 и
и 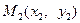 евклидова пространства
евклидова пространства 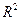 называется число
называется число 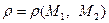 , определяемое формулой:
, определяемое формулой:
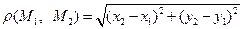 .
.
Множество точек 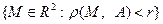 называется открытым кругом радиуса
называется открытым кругом радиуса 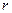 с центром в точке
с центром в точке 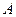 ,
, 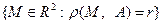 – окружностью радиуса
– окружностью радиуса 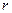 с центром в точке
с центром в точке 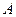 .
.
Открытый круг радиуса 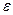 с центром в точке
с центром в точке 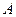 называется
называется 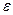 -окрестностью точки
-окрестностью точки 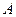 .
.
Определение. Точка 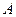 называется внутренней точкой множества
называется внутренней точкой множества 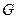 , если существует
, если существует 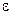 -окрестность
-окрестность 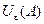 точки
точки 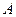 , целиком принадлежащая множеству
, целиком принадлежащая множеству 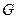 (т.е.
(т.е. 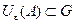 ).
).
Определение. Точка 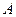 называется граничной точкой множества
называется граничной точкой множества 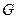 , если в любой ее
, если в любой ее 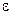 -окрестности содержатся точки, как принадлежащие множеству
-окрестности содержатся точки, как принадлежащие множеству 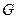 , так и не принадлежащие ему.
, так и не принадлежащие ему.
Замечание. Граничная точка множества может как принадлежать этому множеству, так и не принадлежать ему.
Определение. Множество 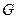 называется открытым, если все его точки – внутренние.
называется открытым, если все его точки – внутренние.
Определение. Множество 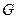 называется замкнутым, если оно содержит все свои граничные точки. Множество всех граничных точек множества
называется замкнутым, если оно содержит все свои граничные точки. Множество всех граничных точек множества 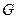 называется его границей (и часто обозначается символом
называется его границей (и часто обозначается символом 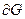 ). Заметим, что множество
). Заметим, что множество 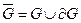 является замкнутым и называется замыканием множества
является замкнутым и называется замыканием множества 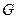 .
.
Пример. Если 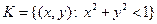 , то
, то 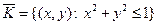 . При этом
. При этом 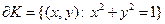 .
.
Определение. Точка 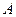 называется предельной точкой множества
называется предельной точкой множества 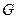 , если в любой
, если в любой 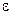 -окрестности точки
-окрестности точки 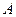 содержатся точки множества
содержатся точки множества 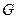 , отличные от
, отличные от 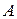 .
.
Замечание. Предельная точка множества может принадлежать, а может не принадлежать этому множеству.
Пример. Множество 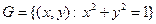 совпадает с множеством своих предельных точек. Множество
совпадает с множеством своих предельных точек. Множество 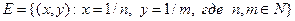 имеет единственную предельную точку
имеет единственную предельную точку 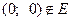 .
.
Предел функции нескольких переменных
Определение. Говорят, что последовательность точек 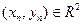 сходится при
сходится при 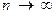 к точке
к точке 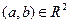 , если
, если 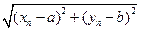 стремится к 0 при
стремится к 0 при 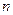 стремящемся к
стремящемся к 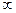 . В этом случае точку
. В этом случае точку 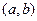 называют пределом указанной последовательности и пишут:
называют пределом указанной последовательности и пишут: 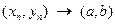 при
при 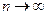 .
.
Можно показать, что 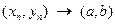 при
при 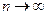 тогда и только тогда, когда одновременно числовая последовательность
тогда и только тогда, когда одновременно числовая последовательность 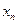 сходится к числу
сходится к числу 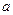 , а числовая последовательность
, а числовая последовательность 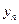 сходится к числу
сходится к числу 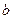 при
при 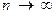 (т.е. сходимость последовательности точек пространства
(т.е. сходимость последовательности точек пространства 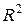 эквивалентна покоординатной сходимости).
эквивалентна покоординатной сходимости).
Пусть 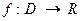 и
и 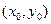 – предельная точка множества
– предельная точка множества  .
.
Определение. Число 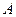 называют пределом функции
называют пределом функции 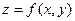 при
при 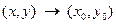 , если для
, если для 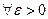
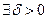 такое, что
такое, что 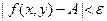 , как только
, как только 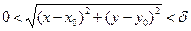 . В этом случае пишут
. В этом случае пишут
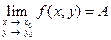 или
или 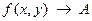 при
при 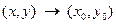 .
.
Замечание.В случае функции одной переменной для существования предела в точке необходимо и достаточно равенство лишь двух чисел – пределов по двум направлениям: справа и слева от предельной точки 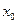 . Для функции двух переменных стремление к предельной точке
. Для функции двух переменных стремление к предельной точке 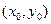 на плоскости
на плоскости 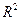 может происходить по бесконечному числу направлений (и необязательно по прямой).
может происходить по бесконечному числу направлений (и необязательно по прямой).
Пример. Найти 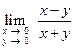 .
.
Пусть стремление к предельной точке 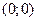 происходит по прямой
происходит по прямой 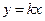 . Тогда
. Тогда
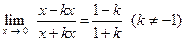 .
.
Предел, очевидно, не существует, так как число 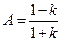 зависит от
зависит от 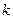 .
.
Пример. Найти 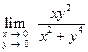 .
.
По любой прямой 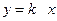 предел один и тот же:
предел один и тот же:
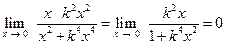 .
.
С другой стороны, пусть стремление к предельной точке происходит по кривой 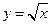 . Тогда
. Тогда
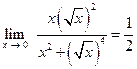 .
.
Следовательно, предела не существует.
Сформулируем понятие предела функции для случая, её аргументы стремятся к к бесконечности. Ограничимся случаем, когда 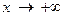 ,
, 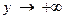 (понятие предела функции в остальных случаях формулируются аналогично).
(понятие предела функции в остальных случаях формулируются аналогично).
Определение. Число 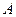 называют пределом функции
называют пределом функции 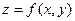 при
при 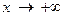 и
и 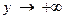 , если для
, если для 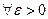
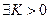 такое, что из неравенств
такое, что из неравенств 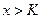 и
и 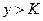 следует неравенство
следует неравенство 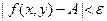 . Этот факт коротко записывают так:
. Этот факт коротко записывают так:
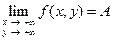 .
.
Теорема. Если существуют 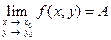 и
и 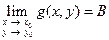 , то
, то
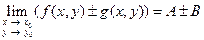 ;
;
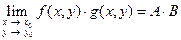 ;
;
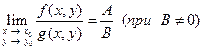 ,
,
где предельная точка 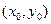 может быть конечной или бесконечной.
может быть конечной или бесконечной.
Справедливы аналоги и других теорем о свойствах пределов функций одной переменной.
