Одну из величин считаем функцией других
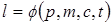 .
.
Для рассматриваемой системы число независимых единиц измерения равно трем (например, для величин p, l, t, т.е. n=3). Применяя 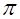 теорему, находят число критериев n-m=5-3=2. Так как размерности всех n физических величин известны, то, составив из них два (так как n-m=2) безразмерных комплекса, получают критерии подобия без написания функциональной зависимости. Получаем
теорему, находят число критериев n-m=5-3=2. Так как размерности всех n физических величин известны, то, составив из них два (так как n-m=2) безразмерных комплекса, получают критерии подобия без написания функциональной зависимости. Получаем
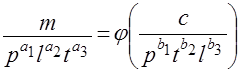 .
.
Для определения неизвестных постоянных a1,a2,…,b1,b2,…, записывают и приравнивают друг другу размерности числителей и знаменателей безразмерных комплексов
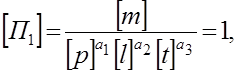
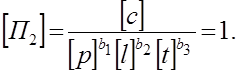
Из данных равенств получают уравнения для определения постоянных: а1=1; а2=-1; а3=2; b1=1; b2=-1; b3=0.
Найденные значения постоянных подставляют в исходную формулу и получают
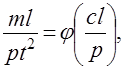 или
или 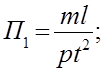
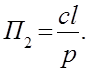
Полученные комплексы являются критериями подобия.
Порядок определения критериев подобия методом анализа размерностей сводится к следующему:
1. Составляют выражения для n-m безразмерных величин П. Для этого в каждое выражение для П одну из n-m величин вводят в числитель с показателем степени, равным единице, а все остальные (от первой до m-й) величины – в знаменатель с неизвестными пока показателями а1, а2,… и т.д. Величины, входящие в знаменатель, выбирают так, чтобы в их размерности по одному разу входили все основные единицы измерения. Величины, входящие в числитель, если n-m меньше числа основных единиц, не должны являться только основными.
2. Из выражений, составленных на основании равенств размерностей соответственных числителей и знаменателей П, определяют показатели степени а1, а2 и т.д.
3. Анализируют критерии и при необходимости для лучшего выявления их физического смысла перемножают или делят некоторые из критериев с охранением их общего числа, равного n-m; записывают один из критериев как функцию остальных m-n-1 критериев.
Метод анализа уравненийосновывается на положении, что у подобных явлений описывающее их уравнения должны быть тождественно равны.
Дифференциальные уравнения движения, например, для механической системы, могут быть записаны в упрощенном варианте следующим образом:
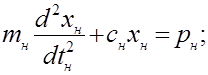
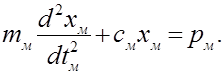
Так как процессы в оригинале и модели подобны, то отношения всех характеризующих их величин должны выражаться с помощью масштабов подобия:
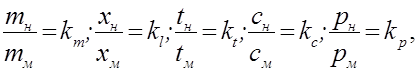
где km,l,t,c,p – масштабы подобия.
Введя выражения km, kl,… в уравнение для модели и разделив все члены уравнения на kp, Pм, получают
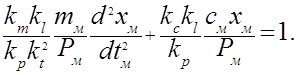
Тождественность полученных уравнений следует из равенства индикаторов подобия единице:
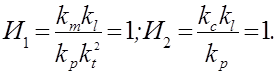
Из совместного рассмотрения выражений находят
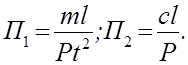
Найденные критерии получаются из дифференциальных уравнений делением всех членов уравнений на один из них, что является следствием приведения уравнений к безразмерному виду при последующем пренебрежении знаками дифференцирования и интегрирования.
Рассмотрим исходное уравнение и разделим все члены уравнения на Р:
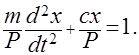
Опускаем знаки дифференцирования, производим сокращения и записываем критериальное уравнение
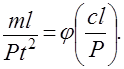
Изложенное является основанием для формулирования общего правила нахождения критериев, которое называют правилом интегральных аналогов:
1) уравнение приводят к безразмерному виду делением всех его членов на какой-либо один из них;
2) опускают знаки дифференцирования и интегрирования;
3) полученные безразмерные комплексы, составленные из переменных величин и параметров, считают критериями подобия;
4) для лучшего выявления физического смысла критериев делят и умножают один из них;
5) записывают один из критериев как функцию n-m-1 получая критериальное уравнение.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1) Первая теорема подобия;
2) Вторая теорема подобия;
3) Третья или обратная теорема подобия;
4) Коэффициенты подобия; индикаторы подобия; критерии подобия;
5) Методы определения критериев подобия;
6) Критериальное уравнение.
