Решение задач №2,3 и 4
Разберем частные случаи решения задач № 2,3,4 и увидим, что же их объединяет между собой.
Задача №2
Построение линии пересечения двух плоскостей значительно упрощается, если одна из плоскостей является проецирующей, т.е. перпендикулярной одной из плоскостей проекций. Проецирующие плоскости проецируются в прямую на плоскость проекций, которой они перпендикулярны. Следовательно, любая прямая, принадлежащая плоскости, проецируется в ту же прямую, что и плоскость.
Исходя из этого, можно утверждать, что если одна из пересекающихся плоскостей проецирующая, то одна проекция линии пересечения известна – она совпадает с прямой, в которую проецируется плоскость.
В задании необходимо построить проекции линии пересечения плоскости треугольника и плоскости параллелограмма. Если параллелограмм проецируется на плоскость проекций в прямую, то вторую проекцию линии пересечения определим из условия принадлежности ее плоскости треугольника (рис.1).
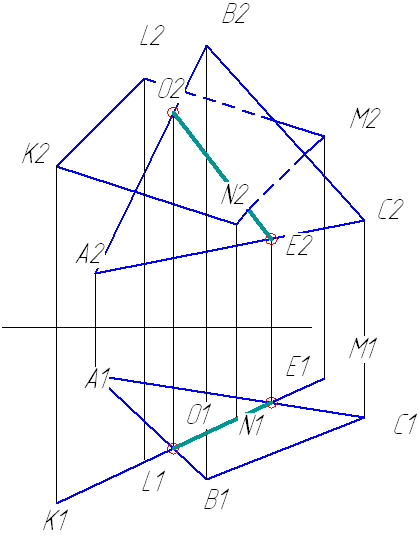
Рис.1
Задача №3
В этой задаче надо построить геометрическое место точек, равноудаленных от плоскости параллелограмма на расстоянии 40 мм, причем площадь его в два раза меньше площади параллелограмма. Прежде надо отметить, что это геометрическое место точек есть плоскость, удаленная от параллелограмма на расстоянии 40 мм и параллельная ему, а т.к. площадь его в два раза меньше площади параллелограмма, то это треугольник, две стороны, которого равны и параллельны сторонам параллелограмма.
Для решения этой задачи надо найти точку в пространстве, удаленную от параллелограмма на расстоянии 40 мм, а затем в ней строить плоскость треугольника. Расстояние от плоскости откладывают по перпендикуляру. Прямая перпендикулярна плоскости, если она перпендикулярна горизонтали и фронтали плоскости. Если плоскость проецирующая, то перпендикуляр к плоскости провести просто, т.к. одна из главных линий плоскости есть прямая проецирующая, а сам перпендикуляр есть прямая уровня. Следовательно:
1) одна проекция его перпендикулярна прямой, в которую проецируется плоскость, а другая проекция параллельна оси Х;
2) т.к. перпендикуляр есть прямая уровня, то по нему можно откладывать расстояния (рис.3).
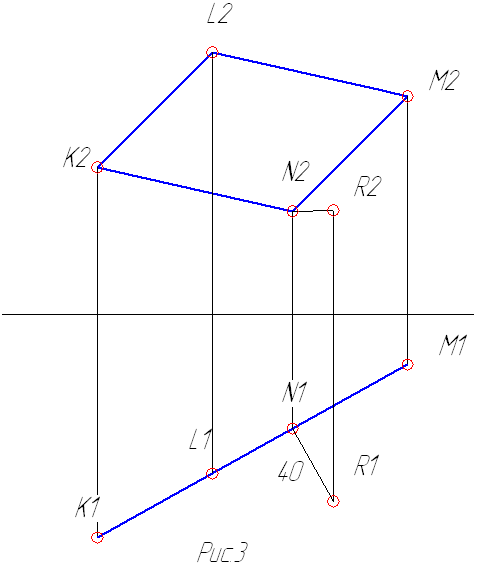
Когда точка найдена, в ней строят плоскость треугольника, стороны которого равны и параллельны сторонам параллелограмма (рис.4).
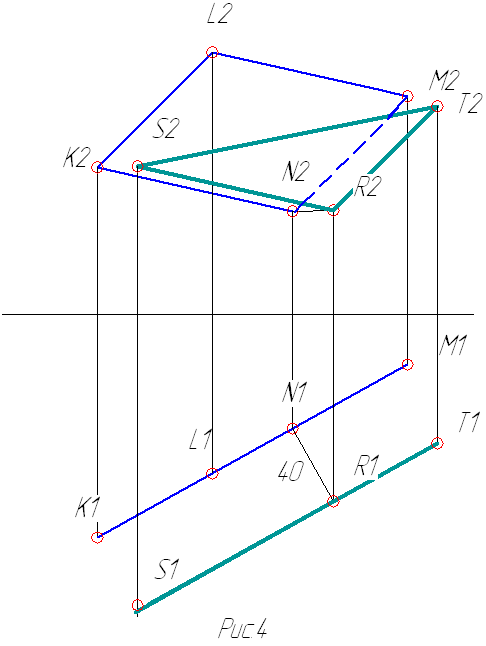
Задача №4
Построение натуральной величины параллелограмма проводится просто, если есть натуральная величина самого параллелограмма. Параллелограмм проецируется на плоскость проекций в натуральную величину, если он параллелен этой плоскости. В этом случае параллелограмм на вторую плоскость проекций проецируется в прямую, т.к. он ей перпендикулярен, и эта прямая располагается параллельно оси Х (рис.5).
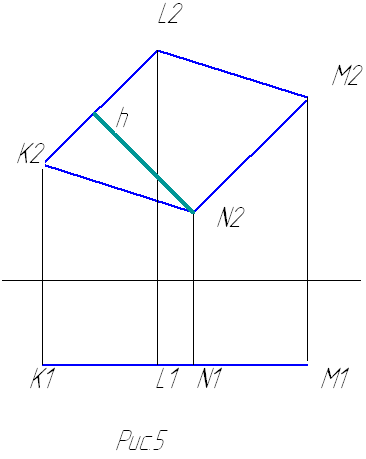
Выводы
Решение разобранных задач показывает, что оно проводится просто, если плоскость занимает частное положение, а именно проецирующее. В задании плоскости заданы в общем виде, т.е. плоскости общего положения. Метод замены плоскостей проекций позволяет преобразовать исходные данные, т.е. свести решение задач к частному виду.
Так как в задачах решение необходимо проводить относительно плоскости параллелограмма ( в 1 задаче – линия пересечения плоскостей, во 2 задаче – ортогональная проекция на плоскость параллелограмма, в 3 задаче – плоскость , параллельная параллелограмму, в 4 задаче – высота параллелограмма), то надо преобразовать параллелограмм общего положения в проецирующий для первых трех задач и далее в параллелограмм уровня для решения последней задачи. Исходя из этого, решение можно проводить на одном чертеже. Для простоты объяснения в методическом пособии разберем выполнение задач на отдельных чертежах.
