Основные теоретические сведения и расчетные формулы
Брус, нагруженный парами сил, плоскости действия которых перпендикулярны его оси, испытывает деформацию кручения. Внутренним силовым фактором в поперечном сечении бруса в этом случае является крутящий момент 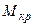 , величину которого определяют методом сечений.
, величину которого определяют методом сечений.
На основании этого метода можно сформулировать правило для определения крутящего момента в сечении бруса: крутящий момент в любом сечении бруса численно равен алгебраической сумме крутящих моментов, расположенных по одну сторону от этого сечения; при этом крутящий момент, приложенный к брусу, считается условно положительным, если при взгляде вдоль оси бруса с левого конца мы видим его направленным по ходу часовой стрелки.
Размеры и форма поперечного сечения бруса в расчетах на кручение учитываются двумя геометрическими характеристиками: полярным моментом инерции 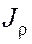 и полярным моментом сопротивления
и полярным моментом сопротивления 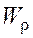 . Для круглого сечения они вычисляются по следующим формулам:
. Для круглого сечения они вычисляются по следующим формулам:
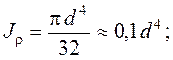 (3.1)
(3.1)
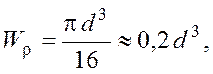 (3.2)
(3.2)
где d - диаметр сечения.
Крутящий момент 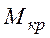 вызывает в сечениях касательные напряжения
вызывает в сечениях касательные напряжения 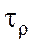 , вычисляемых по формуле
, вычисляемых по формуле
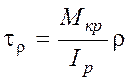 , (3.3)
, (3.3)
где 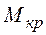 - крутящий момент в сечении бруса;
- крутящий момент в сечении бруса;
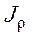 - полярный момент инерции сечения;
- полярный момент инерции сечения;
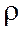 - расстояние от центра тяжести сечения до точки, в которой определяются напряжения.
- расстояние от центра тяжести сечения до точки, в которой определяются напряжения.
Условие прочности записывается в виде
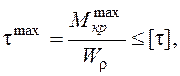 (3.4)
(3.4)
где 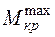 - максимальная по модулю величина крутящего момента, определяемого по эпюре
- максимальная по модулю величина крутящего момента, определяемого по эпюре 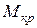 ;
;
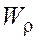 - полярный момент сопротивления;
- полярный момент сопротивления;
[t] - допускаемое касательное напряжение.
Деформация при кручении характеризуется углом закручивания j(рад):
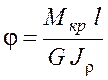 (3.5)
(3.5)
где l- длина бруса;
G - модуль сдвига (модуль упругости второго рода).
Угол закручивания на единице длины бруса называется относительным углом закручивания и вычисляется по формуле
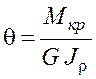 . (3.6)
. (3.6)
Условие жесткости накладывает ограничение на величину относительного угла закручивания:
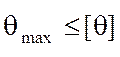 ,
,
где [q] - допускаемый угол закручивания.
Условие жесткости с учетом формулы (3.6) имеет вид
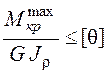 . (3.7)
. (3.7)
Задача
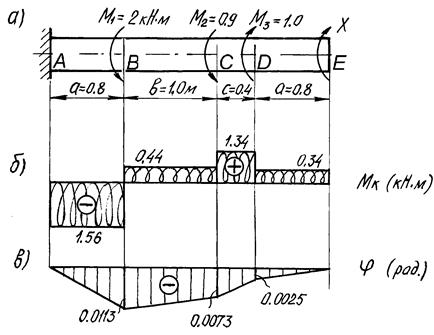
Для заданного бруса круглого сечения (рис. 7, а) определить величину момента X, при котором угол поворота свободного конца бруса равен нулю, построить эпюры крутящих моментов и углов закручивания, подобрать диаметр сечения по условию прочности и произвести проверку бруса на жесткость.
ДАНО :а =0,8 м; в=1,0 м;угол закручивания 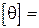 1 град/м;
1 град/м;
с=0,4 м; M1=2 кН× м; M2=0,9кН×м; 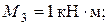 [t]=40 МПа; G=8×104 МПа.
[t]=40 МПа; G=8×104 МПа.
1.Определение величины неизвестного крутящего
момента Х.
Брус жестко заделан левым концом А, правый конец Е свободный. В сеченияхВ, С, и D приложены известные крутящие моменты. Для определения неизвестного момента Х используем условие равенства нулю угла поворота сечения Е.
Угол поворота сечения Е относительно сеченияА определяется как сумма углов закручивания отдельных участков:
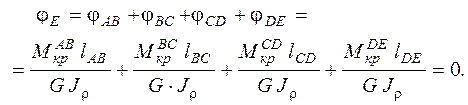 (3.8)
(3.8)
Крутящие моменты 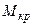 , входящие в выражение (3.8), определяются по приведенному выше правилу.
, входящие в выражение (3.8), определяются по приведенному выше правилу.
Вычисления начинаем с незакрепленного конца:
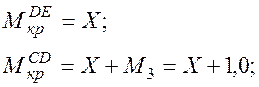
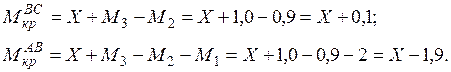 (3.9)
(3.9)
Используя выражения (3.9) и сокращая на 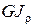 , приводим уравнение (3.8) к виду
, приводим уравнение (3.8) к виду
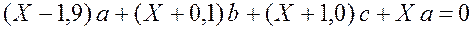 .
.
Подставляя значения a , b , c(рис. 7, а.) и решая это уравнение, получаем Х = 0,34 кН×м.
Примечание: если значение Х получится со знаком минус, направление крутящего момента задано неправильно. В данном примере X положителен, следовательно, направление крутящего момента, показанное на рис.7, правильно.
