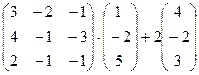Контрольная работа №1

Контрольная работа №1

Системы линейных уравнений
ТЕМА 1. Системы линейных уравнений.

1. Матрицы и действия с ними.

2. Определители и их основные свойства.

3. Методы решения систем линейных уравнений.

СПИСОК ЛИТЕРАТУРЫ

1. Ильин В. А., Позняк Э. Г. Линейная алгебра: Учеб. для вузов.-5-е изд., стер. - М.: Физматлит, 2002. – 317 с.

2. Беклемишев Д. В. Курс линейной алгебры и аналитической геометрии: - М.: Физматлит, 2003. – 303 с.

3. Клетеник Д. В. Сборник задач по аналитической геометрии: Учеб. пособие для втузов / ред. Ефимов Н. В. – 17-е изд., стер. – СПб: Профессия, 2001. – 199 с.

4. Бугров Я.С., Никольский С.М. Высшая математика: Учеб.для вузов: в 3т.-5-е изд., стер.-М.:Дрофа.- (Высшее образование. Современный учебник). т.1. Элементы линейной алгебры и аналитической геометрии.-2003.-284 с.

5. Данко П.Е. и др. Высшая математика в упражнениях и задачах (с решениями): в 2 ч./ Данко П.Е., Попов А.Г., Кожевникова Т.Я -6-е изд..-М.: ОНИКС 21 век, ч.1. -2002.-304 с.

Решение типового варианта контрольной работы.

Задача 1.Вычислить определитель .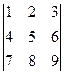

Решение.Для вычисления определителя третьего порядка будем использовать известную формулу Саррюса (правило треугольников), которое может быть записано следующей формулой: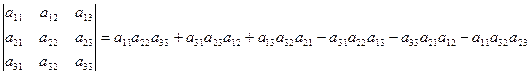

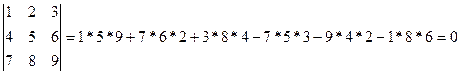
Ответ: 0.

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

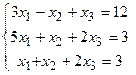
Решение:

Решим систему матричным способом, для этого вычислим обратную матрицу 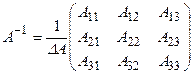, где 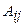- алгебраические дополнения к элементам матрицы.

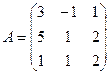
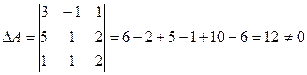- матрица невырожденная.

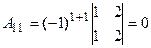
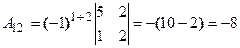
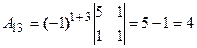
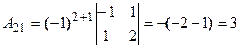
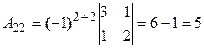
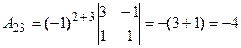
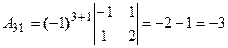
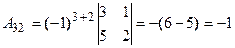
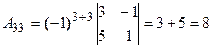
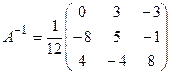
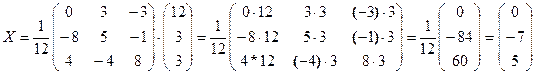
Решим систему методом Крамера. Главный определитель системы:

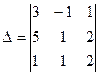. Разложим определитель по элементам первой строки, пользуясь формулой .

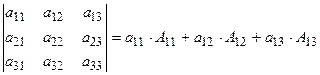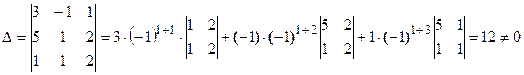
Запишем и вычислим вспомогательные определители

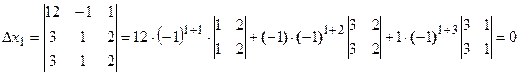
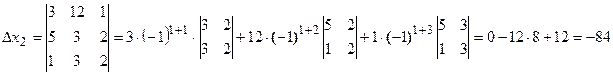
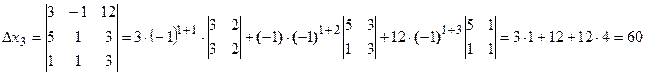Тогда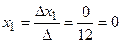

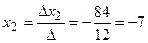
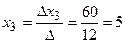
Ответ: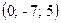

Решим систему методом Гаусса, для этого составим расширенную матрицу системы и упростим ее приведением к треугольному виду.

~ ~ ~

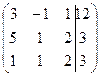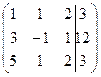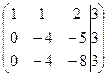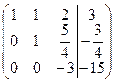
Таким образом, система равносильна системе

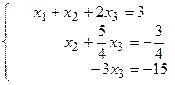
Находим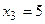

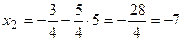
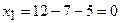
Ответ: , ,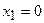

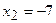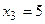
При решении всеми методами одной и той же системы, мы получим один ответ.

Задача 3. Выполнить действия:

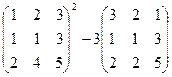
Решение.Выполним решение по действиям.

=

.

.

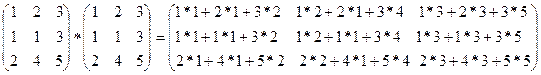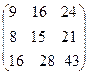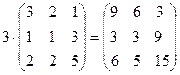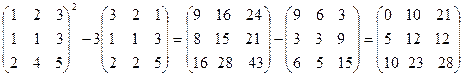
Ответ: .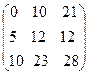

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Если 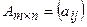, , 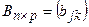то произведением матрицы 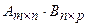называется матрица 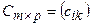, такая, что 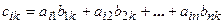, где .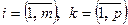

Пример: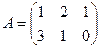

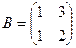
Произведение 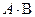не определено, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2).

Произведение 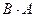определено.

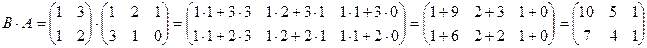
Контрольная работа №1.

Вариант 1

Задача 1. Вычислить определитель:

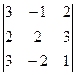
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

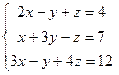
Задача 3. Выполнить действия:

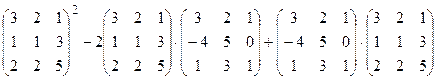
Контрольная работа №1.

Вариант 2

Задача 1. Вычислить определитель:

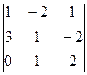
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

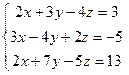
Задача 3. Выполнить действия:

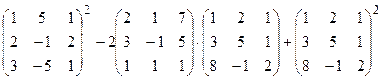
Контрольная работа №1.

Вариант 3

Задача 1. Вычислить определитель:

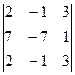
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

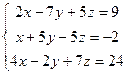
Задача 3. Выполнить действия: