Исследование систем линейных уравнений
Определение. Расширенной матрицей системы называется матрица системы, дополненная столбцом свободных членов. Такая матрица обозначается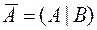 
.
Пусть дана система из m линейных алгебраических уравнений с п неизвестными.
Т е о р е м а 1.5.(Кронекера – Капелли). Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы: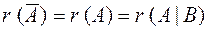 
.
Т е о р е м а 1.6. Если ранг матрицы совместной системы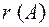 
равен числу неизвестных этой системы, то система имеет единственное решение.
Т е о р е м а 1.7. Если ранг матрицы совместной системы 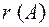меньше числа неизвестных этой системы, то система имеет бесчисленное множество решений.
Для исследования однородной системы линейных уравнений пользуются следующими теоремами:
Т е о р е м а 1.8. Однородная система уравнений всегда совместна.
Т е о р е м а 1.9. Если ранг матрицы 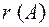равен числу неизвестных п, то xi = 0 – единственное решение.
Т е о р е м а 1.10. Если ранг матрицы 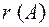меньше числа неизвестных системы п, то система имеет множество решений.
Для того, чтобы решить произвольную систему линейных уравнений, надо:
1. Найти ранг основной и расширенной матриц системы.
2. Если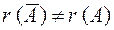 
, то система несовместна.
3. Если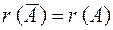 
, то система совместна. Тогда надо найти какой – либо базисный минор порядка r. Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить).
4. Неизвестные, коэффициенты которых входят в базисный минор, называются главными, а остальные (n – r) неизвестные называются свободными. Главные неизвестные оставить слева, а свободные неизвестные перенести в правую часть уравнений.
5. По правилу Крамера найти выражения главных неизвестных через свободные неизвестные и получить общее решение системы.
6. Придавая свободным неизвестным произвольные значения, получить соответствующие значения главных неизвестных. Таким образом, можно найти частные решения исходной системы уравнений.
1.7. Сводная таблица для исследования систем линейных уравнений