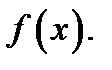Точки экстремума функции. Экстремумы функции. Необходимый признак экстремума. Критические точки. Наибольшее и наименьшее значения функции в замкнутом интервале
Пусть 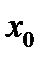 – внутренняя точка области определения функции
– внутренняя точка области определения функции 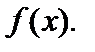 Точка
Точка 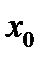 называется точкой максимума функции
называется точкой максимума функции 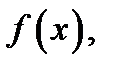 если для всех отличных от
если для всех отличных от 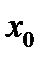 точек некоторой окрестности точки
точек некоторой окрестности точки 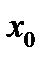 (другими словами, некоторого малого интервала, содержащего внутри себя точку
(другими словами, некоторого малого интервала, содержащего внутри себя точку 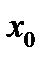 ), выполняется неравенство
), выполняется неравенство 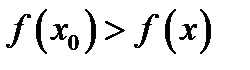 .
.
Точка 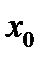 называется точкой минимума функции
называется точкой минимума функции 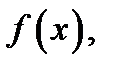 если для всех отличных от
если для всех отличных от 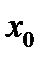 точек некоторой окрестности точки
точек некоторой окрестности точки 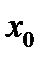 выполняется неравенство
выполняется неравенство 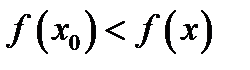 .
.
 Точки максимума и минимума функции называются точками экстремума этой функции, а значения функции в этих точках – экстремальными (максимальными или минимальными) значениями.
Точки максимума и минимума функции называются точками экстремума этой функции, а значения функции в этих точках – экстремальными (максимальными или минимальными) значениями.
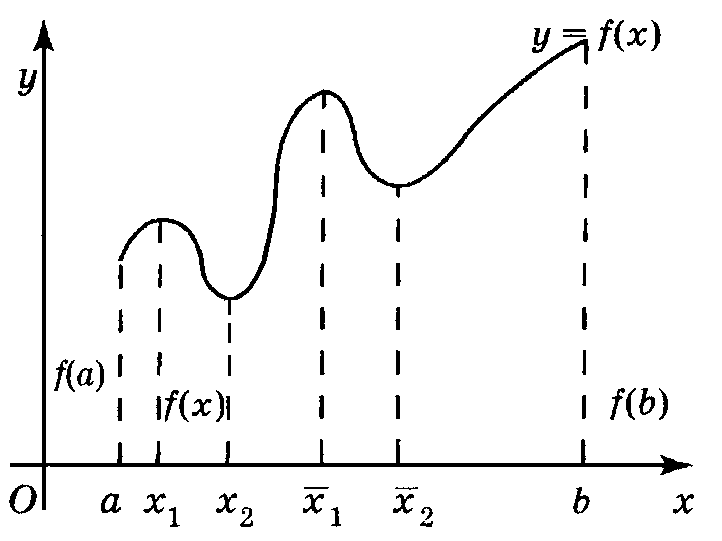
| Рис. 62 |
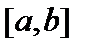 функ-цию, график которой изображён на рис. 62. Для этой функции
функ-цию, график которой изображён на рис. 62. Для этой функции 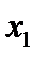 – точка максимума, так как значение
– точка максимума, так как значение 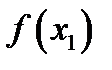 больше значений функции
больше значений функции 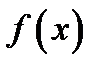 во всех соседних точках, т. е. оно является наибольшим значением функции
во всех соседних точках, т. е. оно является наибольшим значением функции 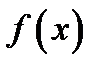 в некоторой окрестности точки
в некоторой окрестности точки 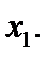 Аналогично
Аналогично 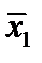 – точка максимума функции
– точка максимума функции 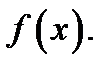 Кроме того,
Кроме того, 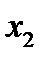 и
и 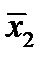 являются точками минимума функции
являются точками минимума функции 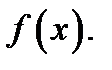 В то же время для функции с графиком, указанным на рисунке, минимальное значение
В то же время для функции с графиком, указанным на рисунке, минимальное значение 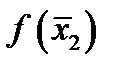 больше
больше 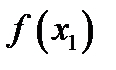 – максимального значения этой функции.
– максимального значения этой функции. Отметим также, что максимальное значение функции, как и минимальное ее значение, определяются для достаточно малого интервала, содержащего точку максимума или минимума функции. Эти значения нельзя путать с наибольшим и наименьшим значениями функции на интервале 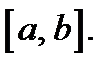 Дело в том, что указанные значения функция может принять на концах интервала. Эти значения могут также совпадать с максимальным и минимальным значениями функции. Например, для функции, график которой указан на рис. 62, наибольшим значением функции в интервале
Дело в том, что указанные значения функция может принять на концах интервала. Эти значения могут также совпадать с максимальным и минимальным значениями функции. Например, для функции, график которой указан на рис. 62, наибольшим значением функции в интервале 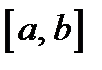 является
является 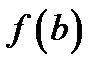 – значение на правом конце интервала, а наименьшее значение функции здесь совпадает с одним из минимальных значений
– значение на правом конце интервала, а наименьшее значение функции здесь совпадает с одним из минимальных значений 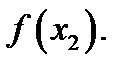
Из сказанного следует, что для нахождения наибольшего и наименьшего значений функции 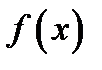 на
на 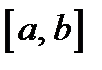 нужно поступить так:
нужно поступить так:
· найти все максимальные и минимальные значения функции в интервале 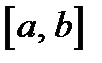 ;
;
· вычислить значения 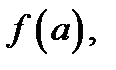
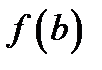 этой функции на концах интервала
этой функции на концах интервала 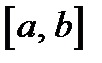 ;
;
· из всех найденных значений выбрать наибольшее, а затем наименьшее.
Эти значения будут соответственно наибольшим и наименьшим значениями функции 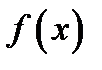 на интервале
на интервале 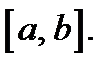
Теорема 3 (необходимый признак экстремума функции).Если дифференцируемая функция 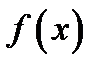 в точке
в точке 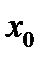 имеет экстремум, то её производная
имеет экстремум, то её производная 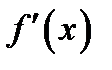 в этой точке обращается в нуль, т. е.
в этой точке обращается в нуль, т. е. 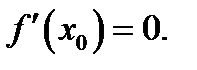
 Доказательство.Пусть
Доказательство.Пусть 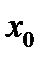 – точка экстремума функции
– точка экстремума функции 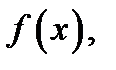 например, точка ее максимума. Это означает, что значение
например, точка ее максимума. Это означает, что значение 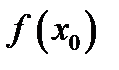 функции в этой точке является наи-большим значением функции в некотором, достаточно малом интер-вале, содержащем внутри себя точку
функции в этой точке является наи-большим значением функции в некотором, достаточно малом интер-вале, содержащем внутри себя точку 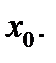 Но тогда согласно теореме Фер-ма производная
Но тогда согласно теореме Фер-ма производная 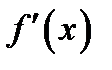 в точке
в точке 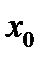 равна нулю, т. е.
равна нулю, т. е. 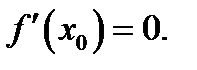 Теоре-ма доказана.
Теоре-ма доказана.
Однако в точке экстремума производная функции 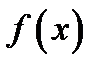 может не существовать. Покажем это на примере функции
может не существовать. Покажем это на примере функции 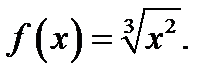 В точке
В точке 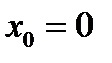 она принимает значение, равное нулю, которое является минимальным значением
она принимает значение, равное нулю, которое является минимальным значением 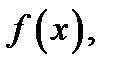 так как значения функции положительны во всех соседних точках
так как значения функции положительны во всех соседних точках 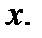 Производная этой функции
Производная этой функции 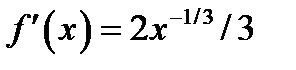 в точке
в точке 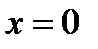 не существует. График функции показан на рис. 63.
не существует. График функции показан на рис. 63.
 Заметим, что не всякая точка, в которой производная функции обращается в нуль или не существует, является точкой экстремума. Покажем это на примере функции
Заметим, что не всякая точка, в которой производная функции обращается в нуль или не существует, является точкой экстремума. Покажем это на примере функции 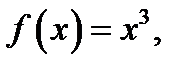 производная которой
производная которой 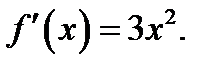 В точке
В точке 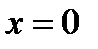 производная обращается в нуль. Но эта точка не является точкой экстремума функции. В самом деле, для всех
производная обращается в нуль. Но эта точка не является точкой экстремума функции. В самом деле, для всех 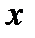 , отличных от нуля, производная
, отличных от нуля, производная 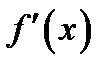 положительна. Отсюда согласно доста-точному признаку возрастания функции получаем, что функция
положительна. Отсюда согласно доста-точному признаку возрастания функции получаем, что функция 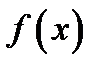 возрастает и слева, и справа от точки
возрастает и слева, и справа от точки 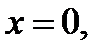 следовательно,
следовательно, 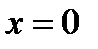 не есть точка экстремума. Эта функция имеет график, показанный на рис. 64.
не есть точка экстремума. Эта функция имеет график, показанный на рис. 64.
Точки, в которых производная 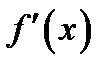 функции
функции 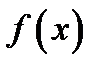 обращается в нуль или не существует, называются критическими точками функции
обращается в нуль или не существует, называются критическими точками функции 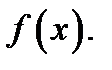 Как мы видели, не всякая критическая точка является точкой экстремума функции
Как мы видели, не всякая критическая точка является точкой экстремума функции