Общий вид линейного уравнения
Линейные уравнения имеют вид: 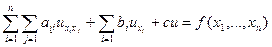 , где коэффициенты
, где коэффициенты 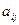 ,
, 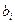 и
и 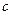 являются функциями только переменных
являются функциями только переменных 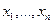 .
.
Если 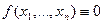 , то это уравнение называется линейным однородным, в противном случае – неоднородным, если коэффициенты
, то это уравнение называется линейным однородным, в противном случае – неоднородным, если коэффициенты 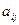 ,
, 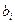 и
и 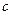 постоянны, то это уравнение называется линейным уравнением с постоянными коэффициентами.
постоянны, то это уравнение называется линейным уравнением с постоянными коэффициентами.
Принадлежность уравнений к тому или иному классу – классификация уравнений – определяется коэффициентами при старших производных. В каждом классе есть простейшие уравнения, которые называют каноническими.
Произведём классификацию уравнений, в которых 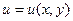 , тогда уравнение, линейные относительно старших производных, можно записать в виде:
, тогда уравнение, линейные относительно старших производных, можно записать в виде: 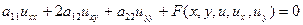 (1),
(1),
а линейные в виде: 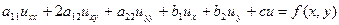 , где коэффициенты
, где коэффициенты 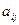 ,
, 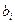 и
и 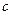 - функции только независимых переменных
- функции только независимых переменных 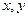 . Любое такое уравнение с помощью замены переменных может быть приведено к более простому – каноническому виду.
. Любое такое уравнение с помощью замены переменных может быть приведено к более простому – каноническому виду.
Сделаем в (1) замену по формулам: 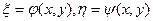 , устанавливающим взаимнооднозначное соответствие между точками
, устанавливающим взаимнооднозначное соответствие между точками 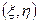 и
и 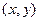 , тогда
, тогда
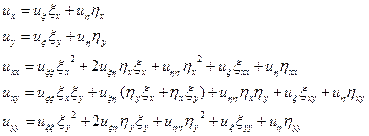 | Тогда получим преобразованное уравнение: 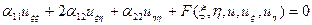 , где , где 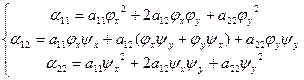 |
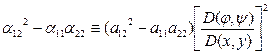 , рассмотрим дискриминант
, рассмотрим дискриминант 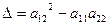
рассмотрим 3 случая:
1. 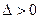 - (1) называется гиперболическим.
- (1) называется гиперболическим. 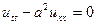
- Δ<0 – (1) называется эллиптическим.
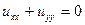
- Δ=0 – (1) называется параболическим.
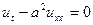
Если (1) гиперболично в области D, то в этой области существуют такие 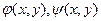 , что уравнение (1) приводиться к канонической форме, заменой
, что уравнение (1) приводиться к канонической форме, заменой 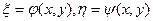 :
: 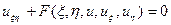 .Причём
.Причём 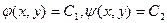 являются общими интегралами о.д.у.
являются общими интегралами о.д.у.
Если (1) эллиптично в области D, то в этой области существуют такие 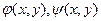 , что уравнение (1) приводиться к канонической форме, заменой переменных
, что уравнение (1) приводиться к канонической форме, заменой переменных 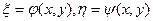 :
: 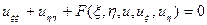
Если (1) параболично в области D, то в этой области существуют такие 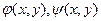 , что уравнение (1) приводиться к канонической форме, заменой
, что уравнение (1) приводиться к канонической форме, заменой 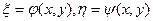 :
: 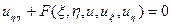
Рассмотрим уравнение: 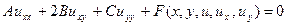
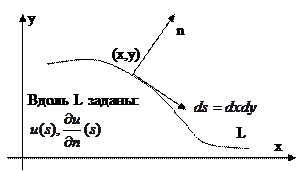 | Хотим задать начальные данные Коши. Разложим в ряд Тейлора: Первый член задан: это функция. Второй член: дифференцируем известные функции: 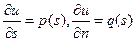 - они известны. Третий член: вторые производные dx, dy – заданы - они известны. Третий член: вторые производные dx, dy – заданы 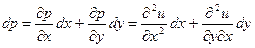 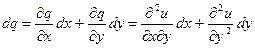 |
Получили систему с тремя неизвестными, нужно третье уравнение, чтобы её решить.
Вспомним про наше уравнение: 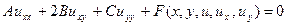
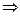
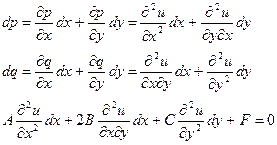 рассмотрим определитель этой системы: рассмотрим определитель этой системы: 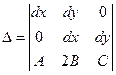 |
Система решается, если определитель не равен нулю, если же он равен нулю, то направления определяемые (dx, dy) характеристические, рассмотрим эту ситуацию.
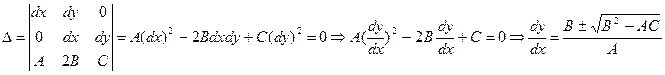
получили, что есть два значения, запрещающие задавать начальные условия, там решение ведёт себя особым образом, мы получим при решении противоречие – это две характеристики.
Рассмотрим три случая:
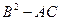 >0 – уравнение гиперболического типа.
>0 – уравнение гиперболического типа. 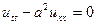
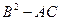 =0 – уравнение параболического типа.
=0 – уравнение параболического типа. 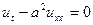
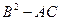 <0 – уравнение эллиптического типа.
<0 – уравнение эллиптического типа. 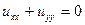
Уравнения, линейные относительно старших производных, можно записать в виде: 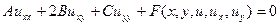 (1),
(1),
Любое такое уравнение с помощью замены переменных может быть приведено к более простому – каноническому виду. Сделаем в (1) замену по формулам: 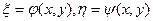 , устанавливающим взаимнооднозначное соответствие между точками
, устанавливающим взаимнооднозначное соответствие между точками 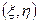 и
и 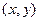 , тогда:
, тогда:
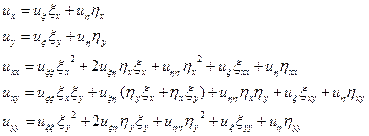 | Тогда получим преобразованное уравнение: 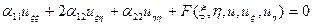 , где , где 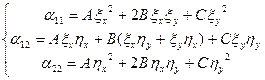 |
