Свойства дифференциала

1. d c = 0;

2. d(c u(x)) = c d u(x);

3. d(u(x) ± v(x)) = d u(x) ± d v(x);

4. d(u(x) v(x)) = v(x) d u(x) + u(x)d v(x);

5. d(u(x) / v(x)) = (v(x) d u(x) - u(x) d v(x)) / v²(x).

Укажем еще на одно свойство, которым обладает дифференциал, но не обладает производная. Рассмотрим функцию y = f(u), где u = φ(x), то есть рассмотрим сложную функцию y = f(φ(x)). Если каждая из функций f и φ являются дифференцируемыми, то производная сложной функции согласно теореме, равна y' = f'(u)· u'. Тогда дифференциал функции

dy = f'(x)dx = f'(u)u'dx = f'(u)du,

так как u'dx = du. То есть

dy = f'(u)du.

(6)

Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала.

Замечание. Отметим, что в формуле (5) dx = ∆ x, а в формуле (6) du является лишь линейной частью приращения функции u.

Рассмотрим выражение для первого дифференциала

dy = f'(x)dx.

Пусть функция, стоящая в правой части, является дифференцируемой функцией в данной точке x. Для этого достаточно, чтобы y = f(x), была дифференцируема два раза в данной точке x, а аргумент либо является независимой переменной, либо представляет собой дважды дифференцируемую функцию.

Дифференциал второго порядка

Определение 1(дифференциал второго порядка).Значение δ(dy) дифференциала от первого дифференциала (5) при δ x = dx, называется вторым дифференциалом функции y = f(x) и обозначается d²y.

Таким образом,

d²y = δ (dy)|_{δ x = dx}.

Дифференциал dⁿy можно ввести по индукции.

Определение 7.Значение δ(d^n-1y) дифференциала от(n-1)-го дифференциала при δ x = dx, называется n-м дифференциалом функции y = f(x) и обозначается dⁿy.

Найдем выражение для d²y при этом рассмотрим два случая, когда x -независимая переменная и когда x = φ(t), то есть является функцией переменной t.

1. пусть x = φ(t), тогда

d² = δ (dy)|_{δx = dx} = δ(f'(x)dx)|_{δx = dx} =

= {δ(f'(x))dx+f'(x)δ(dx)}|_{δx = dx} = f''(x)(dx)²+f'(x)d²x.

Итак,

d2y = f''(x)(dx)2+f'(x)d2x.

(7)

2. пусть x - независимая переменная, тогда

d²y = f''(x)(dx)²,

так как в этом случае δ(dx) = (dx)'δ x = 0.

Аналогично, по индукции легко получить следующую формулу, если x - независимая переменная:

dⁿy = f⁽ⁿ⁾(x)(dx)ⁿ.

Из этой формулы следует, что f⁽ⁿ⁾ = dⁿy/(dx)ⁿ.

В заключение отметим, что дифференциалы второго и более высоких порядков не обладают свойством инвариантности, что сразу видно из формулы для дифференциала второго порядка (7).

Интегральное исчисление функции одной переменной

Неопределенный интеграл.

Функция 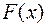называется первообразной по отношению к функции 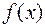, если 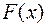дифференцируема и выполняется условие

.

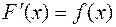Очевидно, что 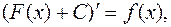где С-любая константа.

Неопределенным интегралом от функции 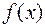называется множество всех первообразных этой функции. Неопределенный интеграл обозначается 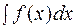и равен

.
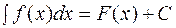