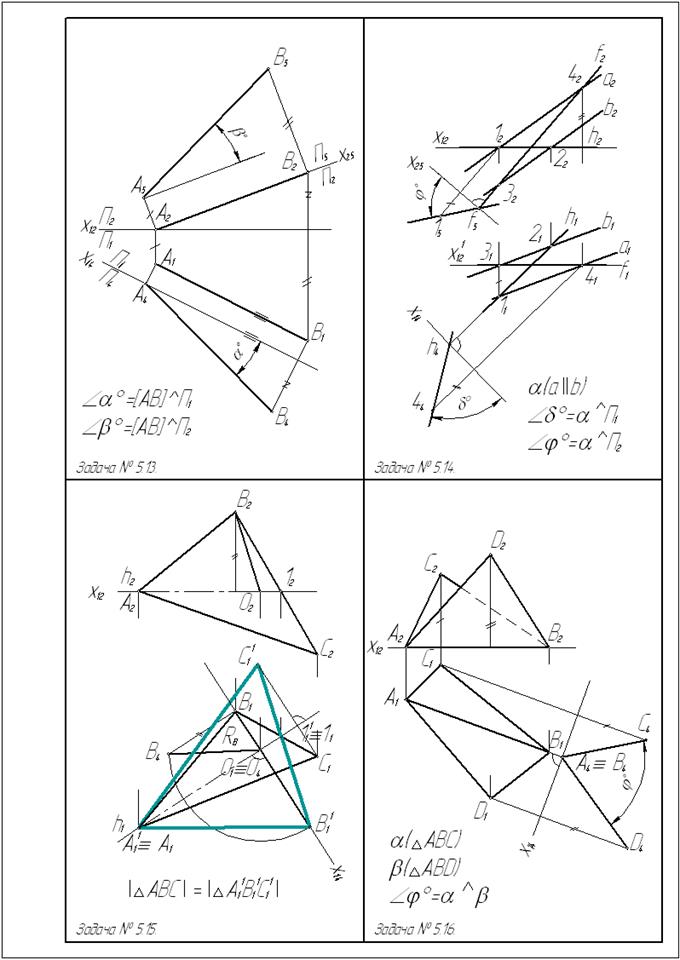
Задача № 5.15. Определить натуральный вид треугольника АВС
. 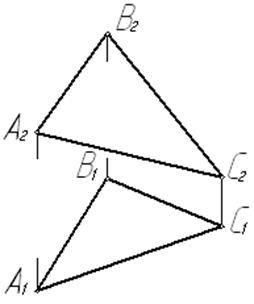
Рис. 41
Такая задача может быть решена или путём построения дополнительных ортогональных проекций АВС( см. задачу № 2.4), или путём поворота плоскости этого треугольника вокруг линии уровня в положение соответствующей плоскости уровня.
Если задаться целью: одним поворотом расположить треугольник параллельно плоскости П1, то за ось вращения следует принять горизонталь (А-1). В тот момент, когда плоскость треугольника будет параллельна П1, горизонтальные проекции каждой из перемещающихся вершин окажутся удаленными от оси вращения на расстоянии, равное радиусу вращения данной точки.
Дальнейшие построения выполняются в такой последовательности:
1) проводим прямые, перпендикулярные А1 - 11, по которым будут перемещаться горизонтальные проекции вращающихся точек;
2) строим проекции радиуса вращения одной из них, например В. Это будут отрезки В1О1 и В2О2;
3) по двум проекциям определяем истинную величину радиуса вращения RB (см. решение задачи № 5.1);
4) отрезок RB откладываем от точки О той прямой, по которой перемещается горизонтальная проекция вершины В;
5) через полученную точку В¢1 и неподвижную 11 проводим прямую до пересечения с прямой, по которой перемещается горизонтальная проекция вершины С;
6) соединяя найденные точки В¢1 и С¢1 друг с другом и с неподвижной вершиной А1, получаем новую горизонтальную проекцию треугольника.
Эта проекция и определяет натуральную величину ∆ АВС.
Фронтальная проекция треугольника окажется преобразованной в прямую, которая совпадает с h2(А2 -12).
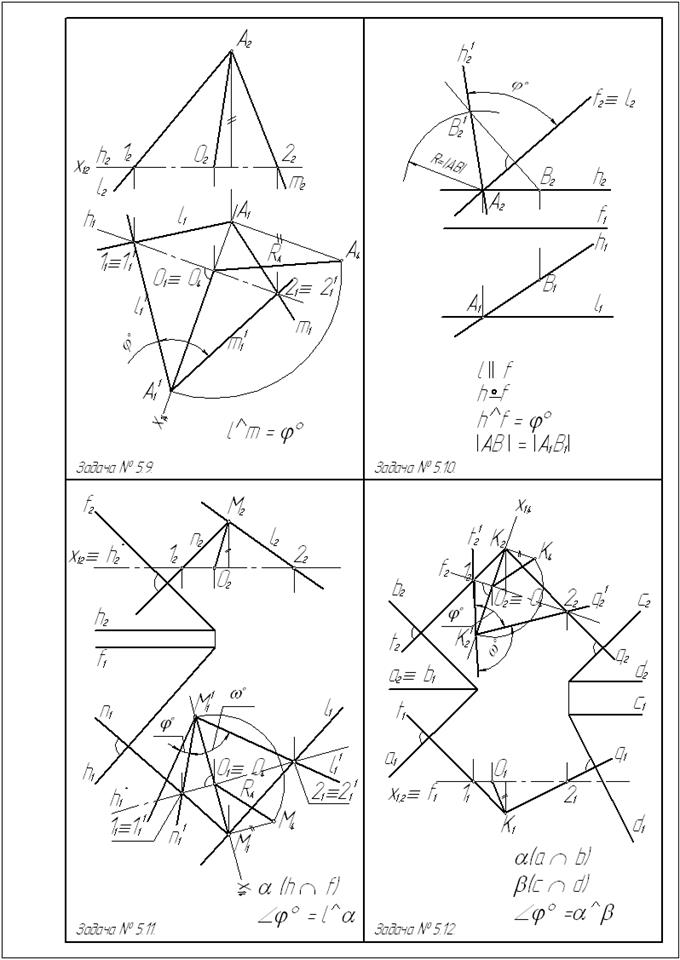
Задача № 5.16. Определить угол j° между плоскостями a(∆ АВС) и β(∆АВD).
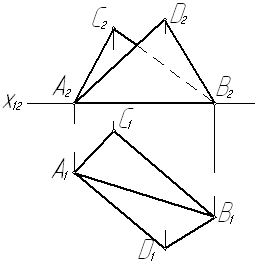
Рис. 42
Углу между двумя плоскостями соответствует линейный угол между прямыми, по которым данные плоскости пересекаются третьей плоскостью, перпендикулярной к линии их пересечения.
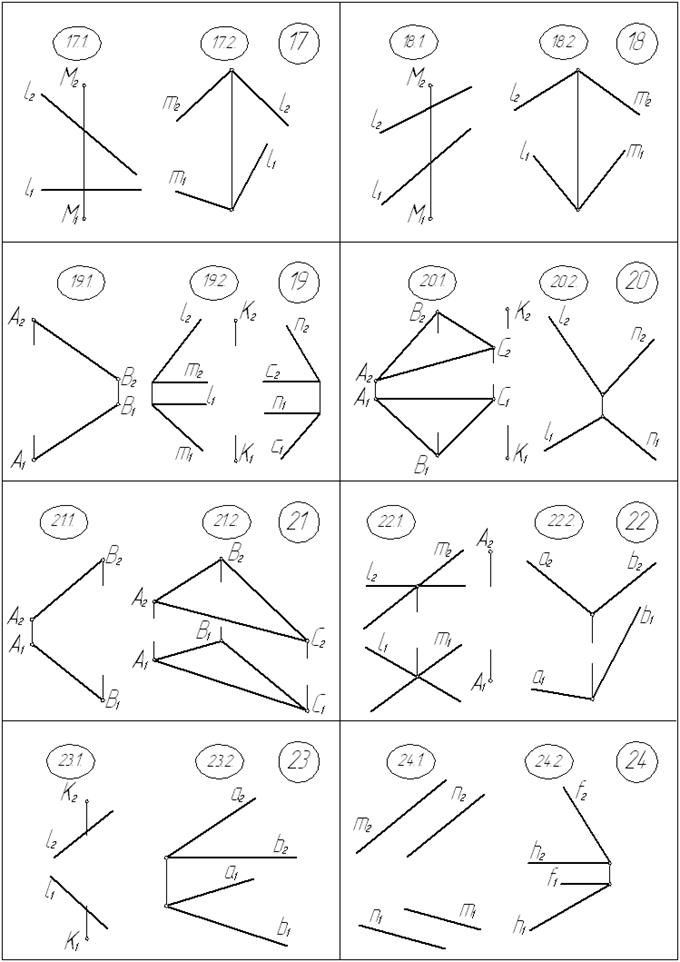
Линия пересечения двух заданных плоскостей a и β есть горизонталь АВ. Чтобы определить угол j° между плоскостями a и β, введем новую дополнительную плоскость П4 ^ АВ. На эпюре новая ось Х14 проводится перпендикулярно к А1В1; плоскость П4, перпендикулярная АВ, будет параллельна сторонам линейного угла, которым измеряется двугранный угол j°.
Решения типовых задач приведены на с. 52…55.
Условия задач
Графические условия метрических задач приведены на с. 59 … 62.
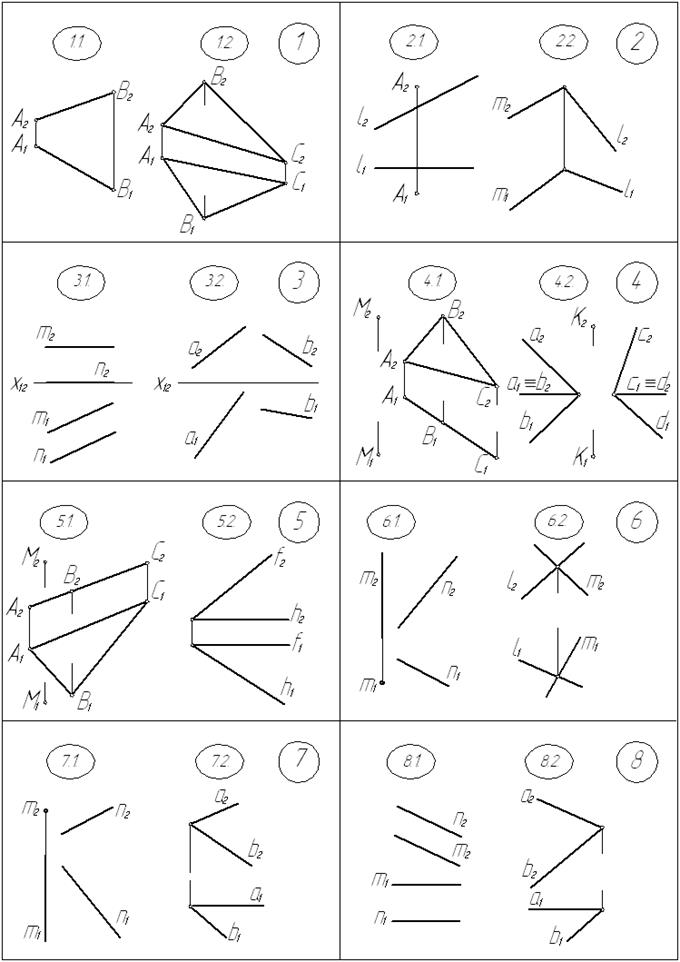
1.1. Определить длину отрезка АВ.
1.2. Определить величину угла наклона плоскости a (∆АВС) к плоскости П1.
2.1. Определить расстояние от точки М до прямой l.
2.2. Определить величину угла между прямыми m и l.
3.1. Определить расстояние между параллельными прямыми m и n.
3.2. Определить величину угла между скрещивающимися прямыми а и b.
4.1. Определить расстояние от точки М до плоскости a (∆АВС),
построить проекции этого отрезка.
4.2. Определить величину угла между плоскостями a (а Ç b) и β (с Ç d).
5.1. Определить расстояние от точки М до плоскости a (∆АВС),
построить проекции этого отрезка.
5.2. Определить величину угла между прямыми h и f.
6.1. Определить расстояние между скрещивающимися прямыми m и n,
построить проекции этого отрезка.
6.2. Определить величину угла между прямыми l и m.
7.1. Определить расстояние между скрещивающимися прямыми m и n,
построить проекции этого отрезка.
7.2. Определить величину угла наклона плоскости a (а Ç b) к плоскости П2.
8.1. Определить расстояние между параллельными прямыми m и n.
8.2. Определить величину угла между прямыми а и b.
9.1. Определить расстояние от точки М до прямой l.
9.2. Определить величину угла между прямыми а и b.
10.1. Определить расстояние от точки М до плоскости a (h Ç f).
10.2. Определить натуральный вид треугольника АВС.
11.1. Определить натуральный вид треугольника АВС.
11.2. Определить величину угла между гранями АВС и АВD.
12.1. Определить расстояние между скрещивающимися прямыми l и m.
12.2. Определить натуральный вид четырехугольника АВСD.
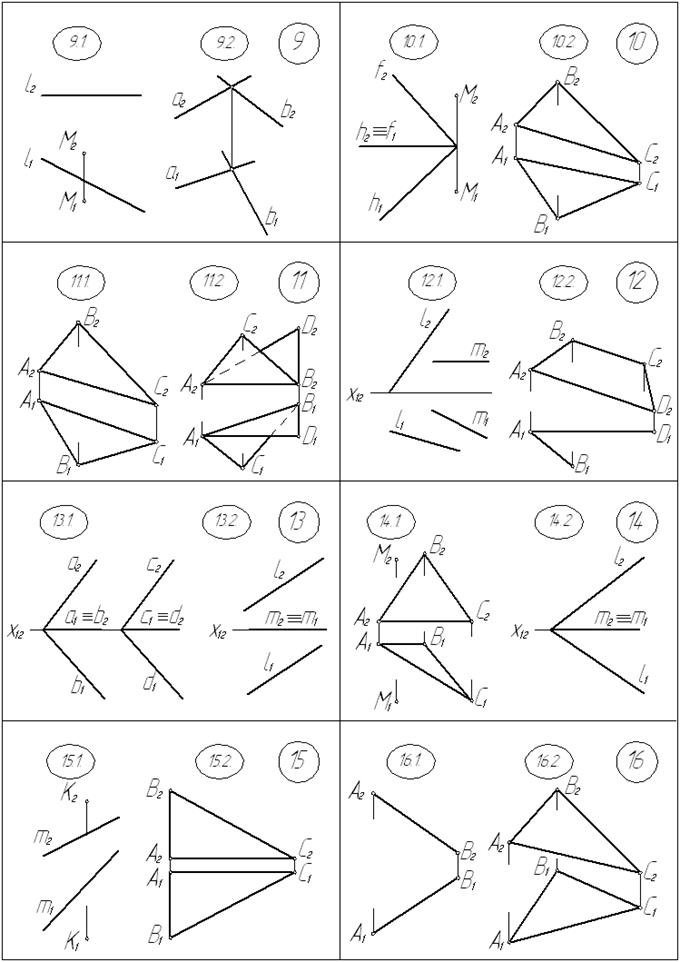
13.1. Определить расстояние между параллельными плоскостями
a ( а Ç b) и β (c Ç d), построить проекции этого отрезка
13.2. Определить величину угла между скрещивающимися прямыми l и m
14.1. Определить расстояние от точки М до плоскости a (∆АВС).
14.2. Определить величину угла между прямыми l и m.
15.1. Определить расстояние от точки К до прямой m.
15.2. Определить натуральный вид треугольника АВС.
16.1. Определить длину отрезка АВ.
16.2. Определить натуральный вид треугольника АВС.
17.1. Определить расстояние от точки М до прямой l.
17.2. Определить величину угла между прямыми m и l.
18.1. Определить расстояние от точки М до прямой l,
построить проекции этого отрезка.
18.2. Определить натуральную величину угла между прямыми l и m.
19.1. Определить длину отрезка АВ.
19.2. Определить величину угла между плоскостями a ( l Ç m), β (n Ç c).
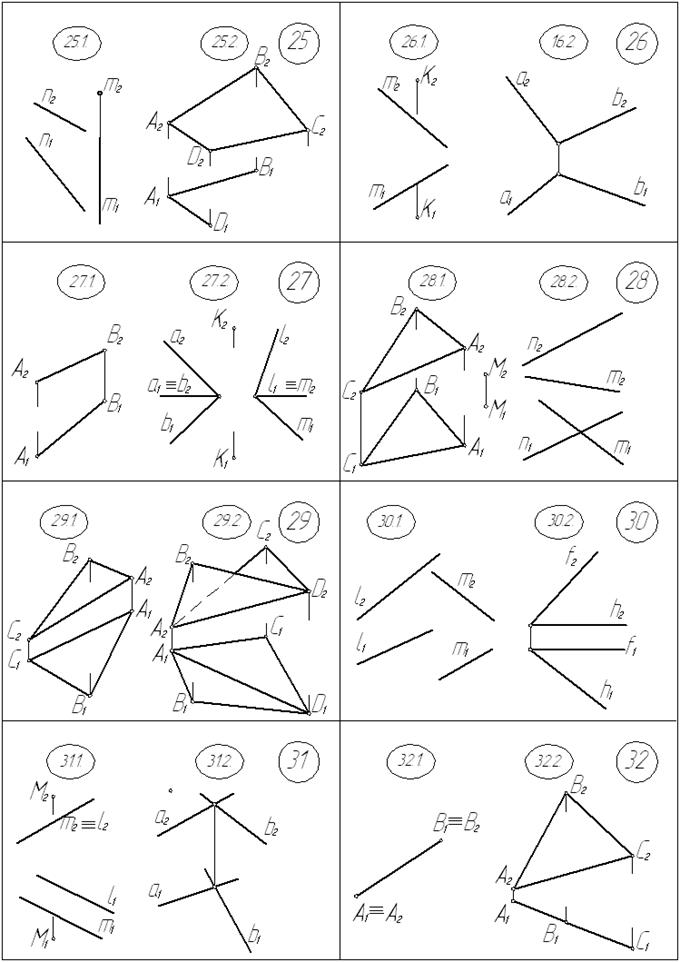
20.1. Определить расстояние от точки К до плоскости a (∆АВС).
20.2. Определить величину угла между прямыми l и n.
21.1. Определить длину отрезка АВ.
21.2. Определить величину наклона плоскости a (∆АВС) плоскости П2.
22.1. Определить расстояние от точки А до плоскости a ( l Ç m) построить
проекции этого отрезка.
22.2. Определить величину угла между прямыми а и b.
23.1. Определить расстояние от точки К до прямой С, построить проекции
этого отрезка.
23.2. Определить величину угла между прямыми а и b
24.1. Определить расстояние между параллельными прямыми m и n.
24.2. Определить величину угла между прямыми f и h.
25.1. Определить расстояние между скрещивающимися прямыми n и m,
построить проекции этого отрезка.
25.2. Определить натуральную величину плоской фигуры АВСD.
26.1. Определить расстояние от точки К до прямой m.
26.2. Определить величину угла между прямыми а и b.
27.1. Определить длину отрезка АВ.
27.2. Определить величину угла между плоскостями h (a Ç b) и β (l Ç m).
28.1. Определить расстояние от точки М до плоскости a (∆АВС), построить
проекции этого отрезка.
28.2. Определить величину угла между скрещивающимися прямыми m и n.
29.1. Определить натуральный вид треугольника АВС.
29.2. Определить величину угла между гранями АВD и ACD.
30.1. Определить расстояние между скрещивающимися прямыми l и m.
30.2. Определить величину угла между прямыми f и h.
31.1. Определить расстояние от точки М до плоскости a (l÷÷ m).
31.2. Определить угол между двумя прямыми а и b.
32.1. Определить длину отрезка АВ.
32.2. Определить натуральный вид треугольника АВС.
ЛИТЕРАТУРА
1. А.Н. Станков, С.В. Борисенкова, Э.В. Солодовникова Начертательная геометрия/ВИТУ. СПб, 1997.
2. Н.Н. Крылов и др. Начертательная геометрия.М.: Высшая школа, 2001.
СОДЕРЖАНИЕ
1. ПРЯМАЯ. ПЛОСКОСТЬ……………………………………………….……3
Условия задач ………………………………………………………………8
2. ДОПОЛНИТЕЛЬНЫЕ ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ……….…. 14
Условия задач
«Дополнительные ортогональные проекции»………………………...... 18
3. ПОЗИЦИОННЫЕ ЗАДАЧИ. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛО-
СКОСТЬЮ, ДВУХ ПЛОСКОСТЕЙ……………………………………...23
Условия задач………………………………………………………………29
4. ПОЗИЦИОННЫЕ ЗАДАЧИ. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ
С ПОВЕРХНОСТЬЮ ………………………………………………………34
Условия задач……………………………………………………………….37
5. МЕТРИЧЕСКИЕ ЗАДАЧИ. ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ И
УГЛОВ. ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОГО ВИДА ПЛОСКОЙ ФИГУРЫ…………………………………………………………………….43
Условия задач ………………………………………………………………56
ЛИТЕРАТУРА………………………………………………………………63
