Построение совершенных нормальных форм с помощью таблиц истинности

Для построения СДНФ или СКНФ , исходя из теоремы о разложении функции алгебры логики от n переменных по k переменным(k=n), можно воспользоваться таблицами истинности.

Для построения СДНФ отметим в таблице истинности те наборы значений переменных, на которых функция равна 1. Для каждого такого набора построим полную правильную элементарную конънкцию по следующей схеме: если значение некоторой компоненты равно 1, то соответствующая переменная входит в элементарную конъюнкцию без отрицания, если значение компоненты 0, то соответствующая переменная входит в элементарную конъюнкцию с отрицанием. Объединив таким образом построенные правильные полные элементарные конъюнкции знаками дизъюнкции, получим совершенную дизъюнктивную нормальную форму.

Для построения СКНФ отметим в таблице истинности те наборы значений переменных, на которых функция равна 0. Для каждого такого набора построим полную правильную элементарную дизъюнкцию по следующей схеме: если значение некоторой компоненты равно 1, то соответствующая переменная входит в элементарную дизъюнкцию с отрицанием, если значение компоненты 0, то соответствующая переменная входит в элементарную дизъюнкцию без отрицания. Объединив таким образом построенные правильные полные элементарные дизъюнкции знаками конъюнкции, получим совершенную конъюктивную нормальную форму.

Построение совершенных нормальных форм , используя принцип двойственности.

Построение совершенной конъюктивной нормальной формы.

Пусть задана некоторая функция алгебры логики от n переменных. Рассмотрим отрицание этой функции и , так как полученная формула будет формулой алгебры логики, то разложим её по n переменным. Полученное выражение, после возможных упрощений, представляет собой совершенную дизъюнктивную нормальную форму. Возьмём отрицания от левой и правой частей полученного выражения. Слева будет исходная функция, а справа (после применения, если это необходимо, закона де Моргана и возможных упрощений) её совершенная конъюктивная нормальная форма.

Построение совершенной дизъюнктивной нормальной формы.

Рассмотрим вместо исходной функции её отрицание и построим для полученной формулы алгебры логики её совершенную конъюктивную нормальную форму. Взяв затем отрицания от левой и правой частей полученного выражения и применив, если это необходимо. закон де Моргана, а так же возможно упростив полученное выражение, получим совершенную дизъюнктивную нормальную форму для исходной функции.

Тавтологии и противоречия. Проблема разрешимости в алгебре логики. Логические следствия.

Формула алгебры логики называется тождественно истиной, общезначимойили тавтологией,если она принимает значение 1 при всех значениях входящих в неё элементарных переменных высказываний. Будем обзначать тавтологию 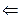F, где F - тождественно истинная формула, а 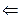-обозначение тавтологии.

Противоречиемили тождественно ложной формулой в алгебре логики называют всякую формулу, которая принимает значение 0 при любых значениях входящих в неё элементарных переменных высказываний.

Формула алгебры логики называется выполнимой,если она принимает одно значение 1 хотя бы на одном наборе значений входящих в неё элементарных переменных высказываний.

Проблема разрешимости в алгебре логикисостоит в том, чтобы найти способ, позволяющий для любой формулы алгебры логики определить, является ли она тождественно истиной.

Очевидно, что эта проблема может быть решена путем построения для заданной формулы таблицы истинности.

Однако, существует более эффективный способ решения этой проблемы.