Некоторые приложения двойного интеграла
Площадь области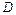 
вычисляется по формуле 
. При переходе в двойном интеграле от прямоугольных координат 
к полярным координатам 
, имеет место формула 
, где 
- область интегрирования в плоскости переменных 
и 
.
Среднее значение непрерывной функции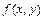 
в области 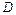вычисляется по формуле 
.
В задачах 10.43-10.48найти площадь области 
, ограниченной указанными линиями:
10.43 
, 
.
10.44 
, 
, 
.
10.45 
, 
, 
.
10.46 
, 
.
10.47 
, 
.
10.48 
, 
, 
, 
.
В задачах 10.49-10.52используя полярные координаты, найти площадь области , ограниченной указанными линиями:
10.49 
, 
, 
, 
.
10.50 
, 
, 
, .
10.51 
, 
.
10.52 
, 
(
).
В задачах 10.53-10.56найти среднее значение функции 
в области 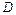, ограниченной указанными линиями, если:
10.53 
, , .
10.54 
, 
, 
.
10.55 
, 
, , 
.
10.56 
.
Объём υ цилиндроида, ограниченного сверху непрерывной поверхностью 
, снизу плоскостью 
и с боков прямой цилиндрической поверхностью, вырезающей на плоскости 
область 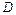, вычисляется по формуле υ 
. При переходе в двойном интеграле от прямоугольных координат к полярным координатам , имеет место формула υ 
, где - область интегрирования в плоскости переменных и .
В задачах 10.57-10.62найти объёмы тел 
, ограниченных следующими поверхностями:
10.57 
, 
, 
, , .
10.58 
, , 
, 
.
10.59 
, , 
, 
.
10.60 
, 
, 
.
10.61 
, , 
, .
10.62 
, , 
.
В задачах 10.63-10.66перейти к полярным координатам и найти объёмы тел , ограниченных поверхностями:
10.63 , , 
, 
.
10.64 
, 
.
10.65 
, , 
.
10.66 
, .
Если 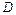- область плоскости , занятая пластинкой, и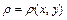 
- плотность пластинки, то статические моменты 
и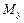 
, моменты инерции 
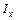и 
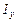относительно осе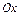й 
и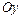 
, масса 
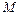, координаты 
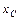и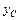 
центра масс 
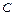пластинки 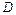вычисляются по формулам:
, 
, 
, 
,
, 
, 
.
Если пластинка однородная, то полагают 
.
В задачах 10.67-10.70найти массу пластинки плотности 
, ограниченной указанными линиями:
10.67 
, 
, 
, 
.
10.68 
, 
, , , 
.
10.69 
, 
, 
, 
,
.
10.70 
, 
, 
, .
10.71Найти массу круглой пластинки радиуса 
, если плотность её пропорциональна квадрату расстояния точки от центра и равна 
на краю пластинки.
10.72Плоское кольцо ограничено двумя концентрическими окружностями, радиусы которых равны соответственно 
и 
. Зная, что плотность материала пропорциональна расстоянию от центра окружностей, найти массу кольца, если плотность на окружности внутреннего круга равна .
10.73Найти статические моменты следующих однородных плоских фигур (плотность 
):
а)прямоугольника со сторонами и 
относительно стороны ;
б)полукруга радиуса 
относительно диаметра;
в)круга радиуса относительно касательной;
г) четверти эллипса с полуосями и 
относительно полуоси .
В задачах 10.74-10.77найти координаты центра масс однородной пластинки плотности , ограниченной линиями:
10.74 , 
, 
. 10.75 
, 
, .
10.76 
, 
. 10.77 
, 
.
10.78Найти моменты инерции следующих однородных плоских фигур (плотность ):
а)прямоугольника со сторонами и относительно стороны ;
б)круга радиуса относительно касательной;
в)треугольника, ограниченного прямыми , 
, относительно оси 
;
г) фигуры, ограниченной эллипсом 
относительно оси .
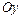10.79На пластинке, лежащей в плоскости 
и занимающей область , распределён электрический заряд с поверхностной плотностью 
. Найти полный заряд пластинки 
, если:
а) 
, , , 
;
б) 
, , , 
.
10.80Распределение давления тела на площадку смятия 
даётся формулой 
. Определить среднее давление тела на эту площадку.
Тройной интеграл.
Пусть функция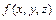 
непрерывна в ограниченной замкнутой пространственной области 
. Если область имеет вид 
, где функции 
, 
- непрерывны и заданы одним аналитическим выражением на отрезке 
, функции 
, 
- непрерывны и заданы одним аналитическим выражением в области 
, являющейся проекцией области на плоскость , то выражение 
называется повторным интегралом от функции 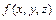по области . Аналогично вводятся другие повторные интегралы.
В повторных интегралах от функции 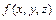последовательно вычисляются простые (однократные) интегралы, причём интегрирование производится по внутренней переменной, а внешние переменные считаются постоянными. В результате последовательных интегрирований получим число.
В задачах 10.81-10.88вычислить повторные интегралы:
10.81 
. 10.82 
.
10.83 
. 10.84 
.
10.85 
. 10.86 
.
10.87 
. 10.88 
.
Тройным интегралом от непрерывной функции 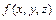по ограниченной замкнутой пространственной области называется число 
, где 
, 
, 
и суммирование ведётся по тем значениям 
, 
и 
, для которых 
.
Замкнутую область 
, где функции , - непрерывны и заданы одним аналитическим выражением в области , являющейся проекцией области на плоскость , будем называть элементарной в направлении оси 
и обозначать 
. Аналогично вводятся элементарные области в направлении других координатных осей.
Вычисление тройного интеграла сводится к последовательному вычислению одного двойного интеграла и одного простого (однократного) или к вычислению трёх простых интегралов.
Тройной интеграл по области 
вычисляется по формуле
.
Если область 
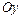- элементарная в направлении оси , т.е. имеет вид 
, где функции , - непрерывны и заданы одним аналитическим выражением на отрезке , то применяют формулу
.
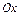Если область - элементарная в направлении оси , т.е. имеет вид 
, где функции 
, 
- непрерывны и заданы одним аналитическим выражением на отрезке 
, то применяют формулу
.
Если не является элементарной, то её представляют в виде объединения непересекающихся (без общих внутренних точек) областей 
, каждая из которых является элементарной в направлении той или другой координатной оси. Разбиение зависит от желаемого порядка расстановки пределов интегрирования. Тогда в силу аддитивности тройного интеграла 
.
В задачах 10.89-10.94вычислить тройные интегралы по областям , ограниченными указанными поверхностями:
10.89 
, . , , , .
10.90 
, 
. , 
, , .
10.91 
, . , .
10.92 
, 
.
10.93 
, , , 
, .
10.94 
, , 
, , .
При переходе в тройном интеграле от прямоугольных координат 
к цилиндрическим координатам 
, связанным с прямоугольными координатами соотношениями 
, 
, 
, имеет место формула
,
где 
-область интегрирования в пространстве переменных 
, и 
.
Если область имеет вид 
, то применяют формулу
.
При переходе в тройном интеграле от прямоугольных координат к сферическим координатам 
( 
-долгота, 
-широта) связанным с прямоугольными координатами соотношениями 
, 
, 
, имеет место формула
,
где -область интегрирования в пространстве переменных , 
и .
Если область имеет вид 
, то применяют формулу 
, где 
.
В задачах 10.95-10.98в тройном интеграле 
перейти к цилиндрическим координатам 
, и расставить пределы интегрирования:
10.95 
.
10.96 
.
10.97 
.
10.98 
.
В задачах 10.99-10.102в тройном интеграле перейти к сферическим координатам 
, и расставить пределы интегрирования:
10.99 
.
10.100 
.
10.101 
.
10.102 
.
В задачах 10.103-10.108перейти к цилиндрическим координатам и вычислить следующие тройные интегралы:
10.103 
, , 
, .
10.104 
, .
10.105 
, .
10.106 
, , .
10.107 
, , 
.
10.108 
В задачах 10.109-10.112перейти к сферическим координатам и вычислить следующие тройные интегралы:
10.109 
.
10.110 
.
10.111 
10.112 
.