Площадь криволинейного сектора
Пусть кривая АВ задана в полярных координатах уравнением
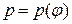
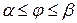 ,
,
причем функция 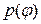 непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке 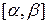 . Плоскую фигуру, ограниченную полярными радиусами, составляющими с полярной осью углы
. Плоскую фигуру, ограниченную полярными радиусами, составляющими с полярной осью углы 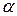 и
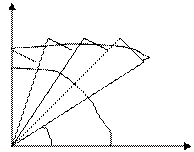
и 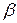 , будем называть криволинейным сектором (рис 1). Площадь криволинейного сектора можно вычислить по формуле
, будем называть криволинейным сектором (рис 1). Площадь криволинейного сектора можно вычислить по формуле
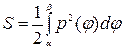
Рис 1.
Билет 21.
Длина дуги плоской кривой
Пусть плоская кривая АВ задана уравнением 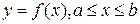 , где f(x) – непрерывная на отрезке [a,b] функция. Разобьем кривую АВ на n произвольных частей точками
, где f(x) – непрерывная на отрезке [a,b] функция. Разобьем кривую АВ на n произвольных частей точками 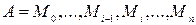 = B в направлении от А к В. Соединив эти точки хордами, получим некоторую вписанную ломаную линию, периметр которой обозначим через Р. Обозначим через li длину одного звена
= B в направлении от А к В. Соединив эти точки хордами, получим некоторую вписанную ломаную линию, периметр которой обозначим через Р. Обозначим через li длину одного звена 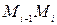 ломаной линии, а через
ломаной линии, а через 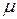 - длину наибольшего из ее звеньев:
- длину наибольшего из ее звеньев: 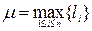
Определение.
Число L называется пределом периметров Р при 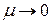 , если для любого
, если для любого 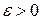 существует
существует 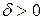 такое, что для всякой ломаной, у которой
такое, что для всякой ломаной, у которой 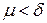 , выполняется неравенство
, выполняется неравенство
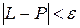
Если при 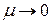 существует конечный предел L периметра Р вписанной в кривую ломаной линии, то этот предел называется длиной дуги
существует конечный предел L периметра Р вписанной в кривую ломаной линии, то этот предел называется длиной дуги 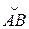 :
:
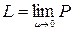
Если функция f(x) непрерывна вместе с f `(x) на отрезке [a,b], то длина дуги выражается формулой
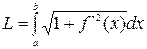
Билет 22.
Площадь поверхности вращения
Площадь поверхности вращения, образующейся при вращении вокруг оси Ox дифференцируемой кривой, определяется по формулам (в зависимости от способа задания кривой)
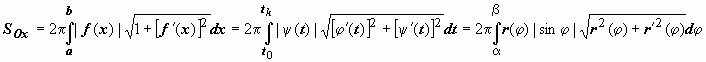 (
( 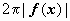 - длина окружности кольца,
- длина окружности кольца, 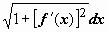 - его ширина).
- его ширина).
 Пример:
Пример:
найти площадь тора, образующегося при вращении окружности 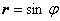 вокруг оси Ox.
вокруг оси Ox.
 Решение:
Решение: 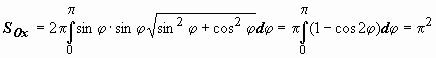 .
.
Билет №24
Вычисление статических моментов, моментов инерции. Координаты центра тяжести
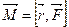
M= 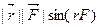 ; Sin(rF)=1; F=ma, |a|=1;
; Sin(rF)=1; F=ma, |a|=1;
M=|r|[m].
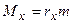 ;
; 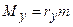
Если M действует на дугу y=f(x):
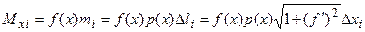
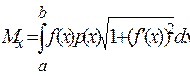 ;
; 
Центр масс: 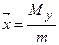
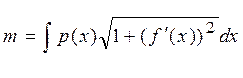
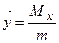 p(x)-плотность
p(x)-плотность
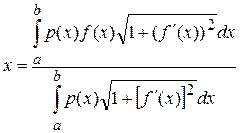
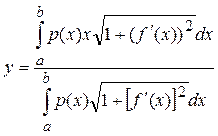
№25Приближенное вычисление
Определенного интеграла
В некоторых случаях не удается точно найти значение определенного интеграла(Определение. Если существует конечный предел интегральных при уменьшении длин отрезков разбиения, то он не зависит от способов разбиения отрезка. Этот предел называется определенным интегралом от функции f(x) по отрезку [a,b] и обозначается 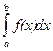 .
.
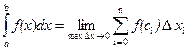 .
.
). Тогда его вычисляют приближенно.
Пусть функция y = f(x) определена и непрерывна на [a,b].
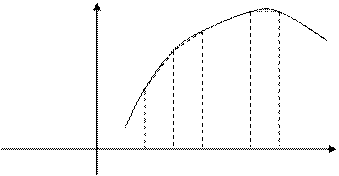 Y
Y
y=f(x)
0 а=х0 х1 х2 х n-1 х n=b X
Разобьем отрезок на n равных частей точками a = x0< x1 < x2 < < ….< xn = b. Обозначим длину отрезка разбиения - 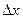 .
.
Мы получаем фигуру, ограниченную ломаной линией, которая с ростом n будет все точнее давать значения площади S криволинейной трапеции. Найдем площадь этой фигуры.
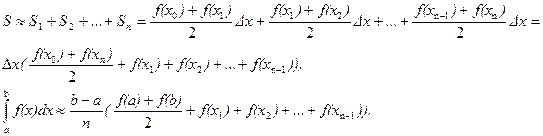
Мы получили формулу трапеций для приближенного вычисления интеграла.
Абсолютная погрешность: 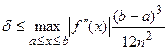
Билет №26
